高中数学微专题压轴题攻略：发散思维、移花接木

我们经常会讲某学生头脑灵活，对数学问题的反应快，对老师的提问有呼应；某学生头脑不灵活，向他提问常是答非所问或根本没有呼应.这种差异是客观存在的，实际上既是对数学概念认识上的差异，更是思维水平上的差异.数学思维是一种极其抽象的逻辑思维，突出体现在研究对象的特征方面，数学对象的特征在于它的抽象是抽象的抽象，没有任何实物(物质的)和能量特征，它只有一个特征：这些对象都处于一定的相互关系之中，处于数量关系、空间关系和类似于这些关系的关系之中，具有思辨性，讲究概念之间相互联系和相互制约，讲究如何理解问题，规划求解步骤，选择最佳解法.

数学发现的思维过程是一个相当复杂的过程，不同的人有不同的思维方式，同一个人发现不同的数学命题也可能有完全不同的思维过程，同一个数学问题，不同的人解答的结果常常是不一样的，这是思维品质的高下决定的，所以要重视数学思维品质的培养，而数学思维品质很广泛，主要表现在深刻性、灵活性、创造性、批判性等方面.如果人脑习惯使用一系列被固化的概念、规则、理论和逻辑抽象形式，这种思维是凝固的，碰到压轴题，受思维定式的影响，往往不会灵活地化解难点，解答过程磕磕碰碰，甚至无法解到最后，形象地说是开不出花，结不了果.人的大脑是一个宝库，人的思维需要开发激活才能不断创造出奇迹，才能开出鲜花、结出果实，所以面对难题我们只有突破思维定式，充分挖掘问题的内涵，从题意中捕捉有用的信息(形象信息、符号信息)进行有效的组合，才能提高我们综合运用知识、调动方法的能力.

发散思维又称为求异思维或辐射思维，是根据一定的知识或事实求得某一问题的各种可能方案的思维，其特点是开放性，方向不同，结果有异.具体表现在如下3个方面.

(1)流畅性.流畅性指心智活动畅通少阻，灵敏迅速，能在短时间内表达较多的概念.流畅性是发散思维的量的指标.

(2)变通性.变通性指思考能随机应变，触类旁通，不局限于某个方面，不受消极定式的约束，能产生新的构想，提出不同的新观念.

(3)独特性.独特性指用以前所未有的新角度、新观点去认识数学知识、反映数学知识，对数学知识、数学问题表现出超乎寻常的独到见解.变通性与独特性是发散思维的质的指标.

通过发散思维，我们可以不断地变更问题，把陌生的问题变更为熟悉的问题，实现知识之间的嫁接，把在这一领域中不易解决的问题变更为另一领域中的问题.我们称之为“移花接木”，从而结出奇异之果.

一、例题精讲

例1　(2018年高考数学江苏卷第21题选做题D)

若x、y、z为实数，且x+2y+2z=6,求x2+y2+z2的最小值.

解题策略　本题是三元问题，要求三元代数式的最小值，如果按照常规通过消元转化为求函数的最小值根本无法操作，命题者的本意是考查柯西不等式的应用，但实际上可以从不同的角度去思考.比如可以通过化整为零巧用二元均值不等式；可以构造向量，利用向量不等式求解；可以利用均值代换；还可以挖掘问题中隐含的几何意义求解或消元后用配方法求解.

解法一　(利用柯西不等式求解)

由柯西不等式，得(x2+y2+z2)(12+22+22)≥(x+2y+2z)2.

∵x+2y+2z=6,∴x2+y2+z2≥4.

当且仅当时不等式取等号，此时

∴x2+y2+z2的最小值为4.

解法二　(化整为零，利用二元均值不等式)

当且仅当时取等号)，　①

当且仅当时取等号)，　②

当且仅当时取等号)，　③

①+②+③,得

当且仅当时x2+y2+z2取得最小值4.

解法三　(构造空间向量，利用不等式求解)

设向量

即

当即(x,y,z)=λ(1,2,2)，且x+2y+2z=6时取等号，

此时

解法四　(均值换元法)

设则

故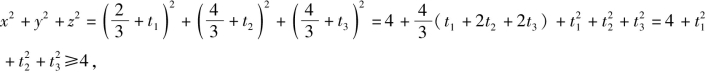当且仅当t1=t2=t3=0时取等号，此时

解法五　(挖掘问题中隐含的几何意义，转化为解析几何问题求解)

设x2+y2+z2=t，则x2+y2=t-z2.

∵直线x+2y+2z-6=0和圆x2+y2=t-z2有公共点，

∴圆心O(0,0)到直线的距离

即

当时取最小值，此时

解法六　(消去x得关于y的一元二次方程，z为参数，用配方法求解)

由x+2y+2z=6，得x=6-2y-2z,

∴x2+y2+z2=(6-2y-2z)2+y2+z2=5y2+5z2+36-24y-24z+8yz

=5y2+(8z-24)y+5z2-24z+36

当3z-4=0且时取等号，此时

例2　在△ABC中，D为边BC上一点， 若△ADC的面积为则∠BAC=________.

解题策略　本例是解斜三角形题型，考查解三角形的知识、方法与技巧.借助辅助线构造特殊三角形是本题的难点，打破思维定式，利用发散思维把角合理拆分能简化运算，从直接解三角形考虑可以有用三角函数定义或用正弦定理或用余弦定理三种不同的解法.若通过移花接木，即把解斜三角形问题嫁接到解析几何或平面向量知识体系求解，实在是两种绝妙的解法.

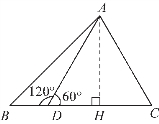
图1-12

解法一　(构造直角三角形，运用三角函数定义解)如图1-12所示，由A作垂线AH⊥BC于H.

(www.xing528.com)

又∵AH⊥BC，∠ADH=60°，∴DH=ADcos60°=1.

又

又在Rt△ABH中，AH=BH，∴∠BAH=45°.

又在Rt△AHC中，

又∠BAC=∠BAH+∠CAH=60°，∴所求角为60°.

解法二　(运用正弦定理解)如图1-12所示，同解法一作辅助线，求得

于是在Rt△AHC中，由得

从而在△ADC中，由正弦定理得

故∠DAC=45°.

又在Rt△ABH中，由得∠ABH=45°⟹∠BAD=∠ADH-∠ABH=60°-45°=15°,

故∠BAC=∠BAD+∠DAC=15°+45°=60°.

解法三　(运用余弦定理解)

如图1-12所示，在△ADC中，由余弦定理得

AC2=AD2+DC2-2AD·DCcos60°

又

又∠ACD=∠BCA，

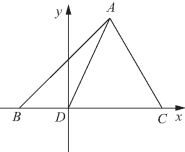
图1-13

∴△ACD∽△BCA，∴∠BAC=∠ADC=60°.

解法四　(运用坐标法解)如图1-13所示，建立平面直角坐标系xDy.

由题设易知

故∠BAC=∠ACx-∠ABC=105°-45°=60°.

解法五　(运用平面向量解)设则

由得

由得

由得故由此得∠BAC=60°.

例3　在平面直角坐标系xOy中，设定点A(a,a)，P是函数图像上一动点，若点P、A之间最短距离为则满足条件的实数a的所有值为________.

解题策略　思考一：PA的长度可用和(a,a)两点之间的距离表示，势必会出现的形式，通过换元求得新元t的取值范围，转化为在新元的范围内对二次函数的分类讨论.

思考二：不难发现P的轨迹是以(a,a)为圆心，为半径的圆，则原问题就转化为圆(x-a)2+(y-a)2=8与曲线相切问题，可利用根的判别式解决.思考二可谓是构造新图形，实现移花接木.

解法一　(运用两点距离公式并通过换元转化为二次函数区间上的最值问题求解)

设则

|PA|2

令得t≥2，|PA|2=t2-2at+2a2-2=(t-a)2+a2-2.

由|PA|取得最小值，当a<2时，

当a≥2时，解得a=-1或

解法二　(构造图形，转化为动圆与双曲线一支相切，利用判别式求解)

若a<0，则a=-1满足题意；

若a>0，则圆(x-a)2+(y-a)2=8与相切.

联立方程组，消去y得

即

令Δ=0，得(2a)2-4(2a2-10)=0，解得

此时方程(*)的解为满足题意.

综上，实数a的所有值为

二、发散训练

1. 函数f(x)=x3+(k-1)x2+(k+5)x-1在区间(0,3)上不单调，求k的取值范围.

2. 已知点P(0,1)，椭圆上两点A、B满足则当m=________时，点B横坐标的绝对值最大.