深化参与式评价，提升数学核心素养

数学核心素养是人用数学观点、数学思维方式和数学方法观察、分析、解决问题的能力及其倾向性，包括数学意识、数学行为、数学思维习惯、兴趣、可能性和品质等。参与式评价不仅包括对学生学习或教师教学的评价，还有对事物发展的评价，通过评价发现事物的本质，寻找事物发展规律，科学且客观地认知事物。

（一）在合作探索中创造新知

学生在合作探索时经历了观察、实验、猜想、证明和评价的过程，这就是思维创新的体现。同时，合作探索活动能让学生更好地理解数学意义和解决问题。例如在教学“组合图形的面积”内容时，教师给出例题信息，让学生独立阅读例题已知信息，观察“房子侧面墙”的形状特点。教师指引学生在小组合作学习中利用折一折、剪一剪、拼一拼等方法，猜想是否能将不规则图形变成已学过的规则图形，最后让学生探索实验后出现的简单图形跟原来图形之间的关系。探索后学生发现，在操作实验过程中将“房子侧面墙”变成了几个已学的简单图形，但是它们之间的面积没有改变。学生通过合作探索，创造了新的数学思维——图形转化思想，为进一步学习几何知识奠定了数学思维基础。

（二）在解决问题中形成策略多样化

新课程改革中要求：“教学内容的呈现应采用不同的表达方式，以满足多样化的学习需求。”这就要求教师在学生解决问题时引导他们从不同的角度进行思考。学生通过合作探索形成了图形转化思想，将复杂不规则图形转化为简单图形。在合作探索中，学生将图形转化成以下几种图形再进行面积计算：

第一种：利用上下拆分方法，将图形拆分为一个三角形和一个正方形（见图3-7-1）。

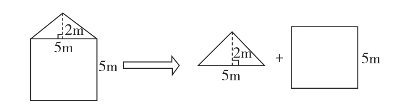
图3-7-1　上下拆分法

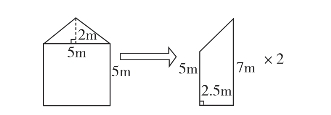
第二种：利用左右拆分方法，将图形拆分为2个梯形（见图3-7-2）。

(www.xing528.com)

图3-7-2　左右拆分法

第三种：在原来图形基础上补充2个小直角三角形（见图3-7-3）。

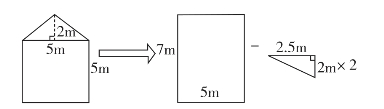
图3-7-3　填补方法

第四种：将图形左右拆分，再旋转和拼接，组合成一个长方形（见图3-7-4）。

图3-7-4　左右拆分后再拼接方法

教师预留充足的时间让学生进行探索和思考。对于不同的思维方法，教师给予学生指导和肯定。对于第一种和第二种转化方法，较多学生能独立完成；对于第三种和第四种转化方法，较少学生能想到。经过观察、分析、比较的学习，学生能掌握多种不一样的解题方法。通过这样的策略多样化展示活动，学生的思维像开闸的洪水一样流畅。在后面的练习中，学生都积极思考更多的解题方法。教师在适当的时候引导学生选择最优方法进行解题，进一步培养学生数学优化思想。

（三）在学习体验中增进情感价值

“组合图形的面积”这一节课，从课前操作练习到课中学习，再到课后的实践问题解决，教师都在引导学生用数学思维观察生活，发现生活中的数学知识，探索生活与数学的联系，促进学生思维能力的成长，加深学生的数学感悟。学生在课前“拼一拼”学习中感悟数学无处不在；在课堂上与同学讲解所拼图形的活动中感悟动手操作的成功感；在知识探索验证活动中感悟数学方法多样化的自豪感；在课后练习中感悟用数学知识解决生活问题的喜悦感。教师只有将学生真正放到学习主体中，让学生充分体验学习，才能让学生真正感悟到数学的学习乐趣，才能有效地提升其数学素养。