知识结构：运用数学史

美国数学史家克莱因指出：“数学史是数学教学的指南。数学史提供了整个数学课程的概貌和数学科学思想体系的发展过程。”目前，小学数学教师在教学实践中运用数学史的情况较少，其根本原因在于大多数教师没有系统地学习数学史，对数学史的教育价值认识不足。数学教师研读数学史，不是为了把数学史知识教授给学生，而是为了更好地教数学。教师在阅读数学史、遴选数学史料和运用数学史的过程中，能优化自身的数学学科知识结构。教师在研究学习了数学史后，了解了数学家们曾经走过哪些弯路、碰到过哪些认知障碍，会对数学教育产生新的感悟。

新课程改革要求数学教师在教学中要有意识地把数学史和教学内容结合起来。把数学史融入课堂，可以运用以下三种方式。

（一）“链接式”的运用

目前，多数教师会在课堂中使用“链接式”方法向学生介绍一些数学史知识。所谓的“链接式”教学，即教师在原有的教学设计外，在课前或课后向学生讲解与本次教学内容相关的数学史知识。例如在教学“认识平行”时，我们可以向学生介绍相关的数学史料。我们的祖先早在3000多年前就认识了平行。我国的《墨经》提出：“平，同高也。”而古希腊的欧几里得在《原本》中是这样论述的：“在同一平面内的直线，向两个方向无限延伸，在不论哪个方向它们都不相交，那就是平行。”教师向学生介绍数学家们是如何解释平行的，有助于帮助学生理解平行的概念。

“链接式”是教师最容易运用的方式。但运用“链接式”时，教师不能仅呈现相关的史料给学生，而要让这些数学史料帮助学生理解所学的知识。

（二）“再现式”的运用

“再现式”指的是教师通过在课堂中创造情境，再现历史的经典时刻，让学生像数学家一样，通过自己的实践和思考去探索新知。例如在教学三角形的面积计算后，教师出示教材第92页“你知道吗？”，向学生介绍我国数学名著《九章算术》中的方田章。

方田章论述了几种平面图形面积的算法，其中记载了三角形的面积计算方式为“半广以乘正从”，如图3-1-2所示。(www.xing528.com)

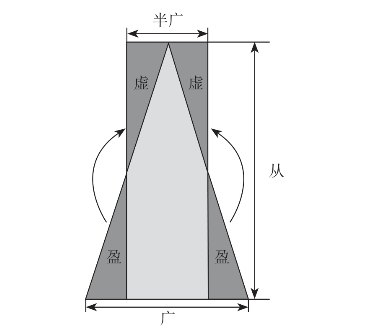
图3-1-2　半广以乘正从

请学生思考古人是怎样计算三角形的面积的，跟我们的推导方法有什么相同的地方。这个过程加深了学生对三角形面积计算推导过程的理解。通过历史时刻的再现，强化学生的认知体验和情感体验，有利于更好地激发学生的学习动机，有利于促进学生更好地进行数学思考，有利于学生更好地理解所学知识。

“再现式”的使用，要求教师在选取数学史料时，不能再简单地复制历史，而要选取与学生的数学认知相近的故事性元素，如历史上有过哪些与本节课相关的经典历史事件。

（三）“融入式”的运用

“融入式”指的是在课堂中融入历史上人类认识产生飞跃的关键进程的方法。历史上人类认识的提升，往往是因为原有的认识无法解决新的问题。教师可以设计一些情境，引导学生经历人类认识的产生、发展的过程，让学生综合运用已有的知识和经验去解决问题。例如在教学“圆的周长”这节课时，教师可以设计动手测量圆周长的活动，让学生探究圆的周长和直径存在怎样的关系。学生不难发现，圆的周长约是直径的3倍。教师顺势而为，向学生介绍圆周率的发展历史。教师在介绍数学家用“割圆术”计算圆周率时，可以借助计算机，向学生动态演示在圆内切割正多边形。通过动态演示，学生如身临其境般感知利用“割圆术”探究圆周率的过程。通过这两个活动，学生经历尝试、探究、分析、反思等过程，积累数学活动经验，也从活动中体会和掌握转化、极限等数学思想方法。学生经历了人类认识的产生、发展过程，对所学知识的理解将会更加深刻。

在课堂教学中融入数学史，教师需要对数学史料进行遴选和再创造。看似困难重重，但只要教师掌握正确的方法便会发现，把数学史巧妙地融入课堂并没有自己想象中那么难。

英国哲学家培根说：“读史使人明智。”通过学习数学发展过程中积淀的深厚历史文化，有助于教师厘清数学知识的发展历史，理解数学的本质和数学知识间的关系，优化自身的数学学科知识结构，提升自身的学科专业知识水平。