圆周率的历史故事

【小知识】

“圆的周长”是人教版小学数学六年级上册第五单元的内容。圆的周长计算在日常生活中有广泛的应用。求圆的周长，可以用卷尺绕圆形物体一圈来测量；拿线绕圆形物体一圈，再测量线的长度；把圆形物体在直尺上滚一圈再量出长度；等等。这几种方法，都是把曲线图形的长度转化为可直接测量的直线段的长度，也就是“化曲为直”。那圆的周长和什么有关呢？不难发现：圆的半径越大，周长就越大。通过测量、计算、找规律等过程，可以发现周长和直径的比值是一个固定的数，叫作圆周率，用字母“π”来表示。

【大背景】

在古代人的日常生产活动中，轮子是重要的发明。随着轮子的广泛使用，人们发现轮子转一圈的长度（即圆的周长）和轮子的直径存在某种联系。古人通过测量不同大小的轮子之后得出结论：圆的周长总是直径的3倍多一点，这便是“古率”。公元前3世纪初，古希腊欧几里得在《几何原本》中提到圆周率是常数；中国的古代数学著作《周髀算经》（约公元前2世纪）中有“径一周三”的说法，也认为圆周率是一个常数。现在，我们都知道圆周率是一个无理数，究竟圆周率是如何从一个常数发展成无理数的呢？

从古代开始，圆周率便迷住了数学家们。在公元前2000年左右，巴比伦人计算出圆周率为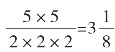，换算成小数为3.125。古埃及人的结论略微不同：，约等于3.143。公元前1650年亚米斯的兰德草卷，测得圆周率的值为，换算成小数为3.16049。

如此粗略的圆周率对于醉心于数学研究的数学家们而言，是远远不够的。公元前250年，阿基米德发明了更精致的计算方法。他采用“穷竭法”来求圆周率，利用略大于圆周和略小于圆周的多边形为圆周率定出上下界。多边形的边数越多，面积越接近圆的面积，得出的上下界就越接近圆周率。但如果正多边形的边非常多，当时计算水平的限制使得阿基米德无法完成计算；如果正多边形的边很少，计算的误差又太大。阿基米德最后用内接于圆和外切于圆的两个正九十六边形为界，计算出：，得出圆周率的精确值应在3.140 8和3.142 9之间。阿基米德计算出圆周率的精确值到小数点后两位。

130年，中国东汉时期的张衡推算出圆周率的数值是（约为3.162 2）。150年，亚历山大港的托勒密计算出圆周率的数值为3.141 6。

263年，中国数学家刘徽在《九章算术注》中提出“割圆”之说。割圆术，就是不断把圆内接正多边形的边数倍增以求出圆周长。刘徽一直算至圆内接正192边形，求得圆周率为3.141 024，也将圆周率算到小数点后两位的精确度。书中还记载了圆周率更精确的值（等于3.141 6）。刘徽断言：“割之弥细，所失弥少。割之又割，以至于不可割，则与圆周合体而无所失矣。”为纪念刘徽的贡献，后人将“3.14”称为徽率。(www.xing528.com)

480年，祖冲之按照刘徽的割圆术之法，设了一个直径为一丈的圆，在圆内切割计算。当他切割到圆的内接192边形时，得到了“徽率”的数值。但他并没有满足于此，继续切割，做了384边形、768边形……一直切割到24 576边形，依次求出每个内接正多边形的边长。最后求得直径为一丈的圆，它的圆周长度在三丈一尺四寸一分五厘九毫二秒七忽到三丈一尺四寸一分五厘九毫二秒六忽之间。也就是说：如果圆的直径为1，祖冲之算出圆周率的数值在3.141 592 6和3.141 592 7之间，相当于精确到小数点后6位，成为当时世界上最先进的成就。祖冲之给出了π的两个分数形式：（约率）和（密率），密率是分母小于16 604的分数中最接近π的。为纪念祖冲之对圆周率发展的贡献，日本数学家三上义夫将这一推算值命名为“祖冲之圆周率”，简称“祖率”。

直到1424年，波斯数学家阿尔·卡西利用3×228边形的多边形，计算出17位π值才打破祖冲之保持了近千年的世界纪录。在此期间，印度天文学家阿耶波多在499年《阿里亚哈塔历书》中使用了3.141 6的数值。意大利数学家斐波那契在1220年利用独立于阿基米德多边形法，计算出圆周率数值为3.141 818。

1579年，法国数学家弗朗索瓦·韦达用3×217边形计算到第9位小数。1593年，弗兰芒数学家阿德里安·范·罗门计算到第15位小数。1596年，荷兰数学家鲁道夫·凡·科伊伦以他超凡的工作量，利用一个262（大约46亿）边形，将圆周率的值精确到了小数点后34位，这个数值被刻在了他的墓碑上。

从17世纪起，新的方法使人们可以计算出更精确的圆周率。大约在1706年，英国天文学家约翰·梅钦将圆周率计算到了小数点后100位。1777年，法国自然学家与数学家布丰提出通过投针来计算π。布丰投针2212次，其中针与平行线相交704次，求得π≈=3.142。

在19世纪，英国业余数学家威廉·香克斯花了15年时间，将圆周率计算到了小数点后707位。不幸的是，其中有180位是错的。1844年，德国学者约翰·达思用不到两个月的时间算出了小数点后的200位。一个世纪之后，英国数学家D.F.弗格森用一台数字计算器计算到了808位。目前，人类对圆周率的计算可以到小数点后1012位，而且根据计算机的能力，我们很容易得到更高的精度，不过却没有实际的用处。

π的来历又是如何呢？1706年，英国数学家琼斯在《新数学引论》中，首次提出用π表示圆周率。但由于琼斯的名气太小，这个简单明了的符号，迟迟得不到推广应用。30年后的1736年，瑞士数学家莱昂哈德·欧拉提倡用π表示圆周率，因权威效应，圆周率符号“π”成为国际通用符号。