圆的面积计算的历史故事-揭秘成果

【小知识】

什么是圆？在小学人教版的教材中没有给出圆的具体定义，只是通过圆规画圆，得到圆的直观定义。在中学的教材中是这样定义圆的：在同一平面内，到定点的距离等于定长的点集合叫作圆。这个定点叫作圆的圆心，用字母O表示，定长叫作圆的半径，用字母r表示。圆的周长=2πr，圆的面积，l表示圆的周长，根据d（圆的直径）=2r，又可以得到圆的面积=。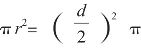

【大背景】

最早得出圆的面积计算公式的是我国古代杰出的数学家刘徽——中国数学史上的牛顿。他用割圆术证明了圆的面积计算，并在《九章算术注》中给出精确的计算公式——“今有圆田，周三十步，径十步。问为田几何？答曰：七十五步。半周半径相乘得积步。”

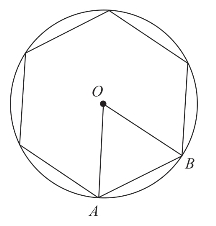
图2-1-1　圆的内接正六边形

在刘徽之前，人们是这样计算圆的面积的：将圆周六等分，依次连接各等分点生成圆的内接正六边形，将内接正六边形的周长作为圆的周长（见图2-1-1）。记圆半径|OA|=r，正六边形的边长为a6，则圆的直径为2r，正六边形的周长为6a6，因为△OAB是个等边三角形，所以圆的半径等于内接正六边形的边长，圆的周长：直径=6a6∶2r=6r∶2r=3∶1，“周三径一”因此而来。然后将六等分的每段弧平均分成2份（见图2-1-2），依次连接12个点形成内接正十二边形，用内接正十二边形的面积代替圆的面积（见图2-1-3）。利用出入相补原理，将圆内接正十二边形剪拼成一个长方形（见图2-1-4），利用长方形的面积来计算圆的面积。这个长方形的长是圆周长的一半，也就是圆内接正六边形周长的一半，长方形的宽是圆的半径。

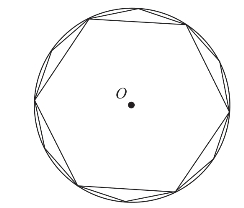
图2-1-2　连接每段弧的中点

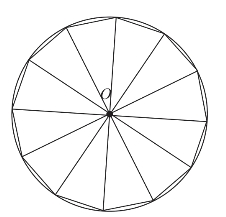
图2-1-3　内接正十二边形

(www.xing528.com)

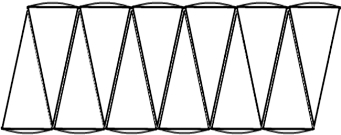
图2-1-4　剪拼成近似长方形

从图中可以看出，圆的面积=圆内接正十二边形的面积+12个弓形的面积，计算出来的面积会小于实际的面积。显然，这样对圆进行分割、拼补得到的结果并不精确。

后来，刘徽改进了前人的算法，将圆内接正六边形的周长看作圆的周长，将圆内接正十二边形的面积看作圆的面积（见图2-1-5）。记圆的半径|OB|=r，圆内接正六边形的边长为a6，将圆内接正十二边形分割成12个全等的三角形，其中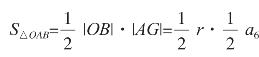，那么圆内接正十二边形的面积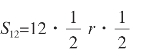a6=3a6r。S2n表示正2n边形的面积（近似圆的面积），表示正n边的周长的一半（近似圆周长的一半），当分割的次数越来越多时，分割得到的圆弧就越来越短，趋于线段。如果不停地分割下去，每一段圆弧都会“化曲为直”，与圆的内接正多边形的边长重合，最后圆的内接正多边形的面积、周长都与圆相等，因此得到圆的面积周长×半径。

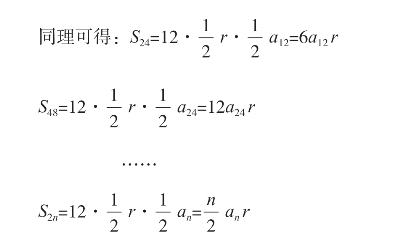
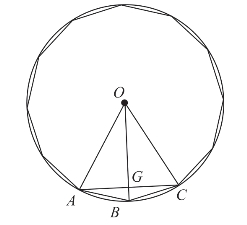
图2-1-5　分割内接正六边形

结合出入相补原理和刘徽的“割圆术”同样可以验证圆的面积计算公式，即把一个圆平均分成若干份，每一份近似于一个等腰三角形，用这些“等腰三角形”可以近似地拼成一个平行四边形（见图2-1-6）。把这个圆平均分的份数越多，拼成的平行四边形就越接近长方形（见图2-1-7）。长方形的长近似于圆周长的一半，长方形的宽近似于圆的半径。因为长方形的面积=长×宽，所以圆的面积周长×半径。这也是我们现在课堂上推导圆面积公式常用的方法。

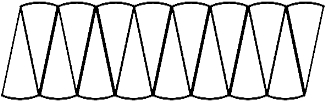
图2-1-6　剪拼成近似平行四边形

图2-1-7　平均分成64份拼成的形状