COX 模型是目前生存分析多因素预后评价中较好的统计方法。在动物科学中经常会遇到“时间—反应”类型资料,如细胞生存期、狂犬病等疾病的潜伏期、药物试验的生效时间等,对这种类型的资料可用各种参数或非参数方法进行分析,但都有一定的局限性。COX 模型以半参数方式出现,适用于许多分布未知的资料和多因素分析,可以在众多预后因素共存的情况下,排除混杂因子的影响,提高预后分析的质量,并能处理截尾数据。
在SAS 统计系统中,可以利用PROC PHREG 过程对生存数据进行回归分析,因变量为生存时间,可以处理有截尾数据的生存时间。模型中的自变量可以是连续性变量、分类变量、时间依存的自变量。可以对比例风险模型是否成立作出检验,利用最大似然法迭代求出模型的参数估计,对模型的参数做似然比、比分和Wald 等检验。
(一)调用格式
PROC HPREG DATA=选项列表;
MODEL 生存时间变量∗截尾指示变量(数值)=自变量名/选项列表;
STRATA 分组变量名列表;
FREQ 变量名列表;
BY 变量名列表。
(二)语句说明
1.MODEL 语句
定义生存时间和截尾指示变量及说明变量:NOPRINT,不打印输出;NOSUMMARY,不打印输出事件和截尾数值;SIMPLE,输出MODEL 语句中每一个说明变量的简单统计量。
①TISE=方法,指定估计生存率所用的方法:BRESLOW,使用Breslow 的近似似然估计,为默认的选项;DISCRETE,用离散Logistic 模型替代比例风险模型,多用于m:n 的Logistic 回归;EFRON,使用Efron 的近似似然。
②EXACT,计算在比例危险假定下所有失效事件发生在具有相同值缺失事件或较大值时间之前的精确条件概率。
③ENTRYTIME=变量名列,规定一个替代左截断时间的变量名。
④SELECTION= method,方法可以选择以下几种:FORWARD(或F),按照规定的P 值SLE 从无到有依次选一个变量进入模型;BACKWARD,按照规定的P 值SLS 从含有全部变量的模型开始,依次剔除一个变量;SCORE,采用最优子集选择法,其中SLE 选择项用于指定协变量进入模型的显著水平,SLS 选项用于指定协变量停留在模型中的显著水平,缺省值皆为0.05。
2.STRATA 语句
比例风险的假设可能不会对所有的层都成立,此时需要作分层分析。STRATA 语句要求按照分层变量名列的水平数拟合一个多层的COX 模型。与BY 语句不同,后者是要求按分组变量名估计模型及参数。
(三)实例应用
例11.3 连续监控25 只分别以A、B 两种不同兽药治疗藏系绵羊某种疾病肺脏细胞培养情况,观察细胞膜存活时间,资料见表11.2, +为截尾值,1:细胞膜破损,0:细胞膜无破损,请试做COX 回归分析。
表11.2 25 只藏系绵羊肺脏细胞培养情况数据表
 (https://www.xing528.com)
(https://www.xing528.com)
SAS 程序如图11.11 所示。
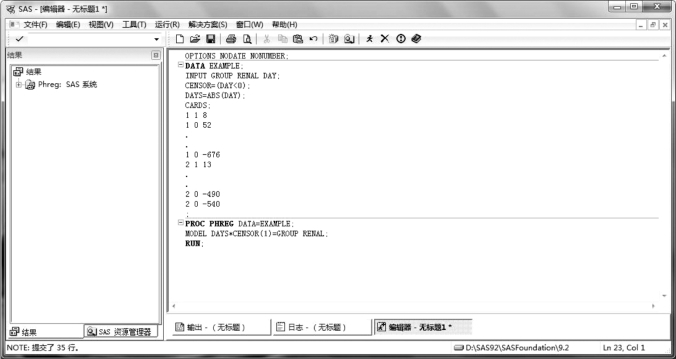
图11.11 例11.3SAS 程序图(1)
结果输出为:
1.输入数据信息
本部分输出结果为截尾事件和终点事件。本题中截尾数据5 例(20%),SAS 程序如图11.12 所示。

图11.12 例11.3SAS 程序图(2)
2.模型检验结果
本部分结果表明,模型较好地拟合了研究数据,有统计学意义(P <0.01),SAS 程序如图11.13 所示。
3.参数检验结果及统计量描述
本部分结果包括参数估计值、标准误、Wald 卡方值、P 值、相对危险比。变量RENAL 在统计学上有显著性差异(P=0.000 3)。HR=36.852,可以认为有细胞破裂损坏的概率是没有细胞破裂损坏的61.081 倍。变量GROUP 在统计学意义上没有显著性差异(P=0.058 7),尚不能认为A、B 两种兽药对研究对象的生存时间的影响有显著性差异,但有显著性变化趋势。

图11.13 例11.3SAS 程序图(3)
根据参数估计值,可以写出以下COX 回归方程:
h(t,x)=h0(t)exp(0.989 73∗group+4.112∗renal)
由此可得,不同的兽药和细胞膜破裂的相对危害度分别为2.690 和61.081,说明B 兽药死亡的危险是A 兽药的2.690 倍(P=0.057 8,有显著性差异趋势),而有细胞破裂的死亡危险为无细胞破裂损害的61.081 倍。
SAS 程序如图11.14 所示。

图11.14 例11.3SAS 程序图(4)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




