主成分分析实例应用-SAS统计分析实用教程

例10.1　某兽医研究所通过10 只藏羊的4 项高原低氧适应性指标：SOD、GSH、MDA 和TAOC，分别用A 至D 表示，数据见表10.1，试进行主成分分析。

表10.1　10 只藏羊的4 项高原低氧适应性指标数据

SAS 程序如图10.1 所示。

图10.1　例10.1SAS 程序图（1）

输出结果为：

1.分析变量的简单统计量

本部分结果分别计算每一个分析变量的平均数和标准差。例如，10 只藏羊血液指标SOD的平均数和标准差分别为133.000 0 和100.559 5。

SAS 程序如图10.2 所示。

图10.2　例10.1SAS 程序图（2）

2.所有分析变量间的相关系数矩阵

该部分结果给出了所有4 个分析变量彼此间的相关系数。其中，A 和B 间的相关系数最大（0.822 7），而B 和C 间的相关系数最小（0.012 3）。

SAS 程序如图10.3 所示。

图10.3　例10.1SAS 程序图（3）

3.相关系数矩阵的特征值、贡献率（每个特征值所解释的方差的比例）及累计贡献率（所解释的方差累计比例）

本部分结果可得，所有主成分的方差（特征值）分别为：2.555 0，1.050 1，0.285 4 和0.109 4；贡献率分别为0.638 8，0.262 5，0.071 4 和0.027 4，前2 个主成分的累计贡献率达到了0.901 3，表明这两个主成分包含了原来4 个指标的90.13%的信息量。

SAS 程序如图10.4 所示。

图10.4　例10.1SAS 程序图（4）

4.特征向量

该部分结果给出的是所有4 个主成分相应的特征向量。每个变量所对应的特征向量值实际上就是用这些变量预测某一主成分的回归系数。

SAS 程序如图10.5 所示。

图10.5　例10.1SAS 程序图（5）

根据计算出的特征向量，可写出由标准化变量所表达的前两个主成分的关系式：

第1 主成分：Z1=0.582 3A+0.581 4B+0.147 1C+0.548 9D

第2 主成分：Z2=0.167 9A-0.210 0B+0.940 5C-0.207 8D

在第1 主成分中，相关系数从大到小依次为SOD（A），GSH（B），TAOC（D）和DMA（C），因此，第1 主成分反映了当该主成分的值较大时，4 个指标的数值均会增大，增大的程度与相关系数大小趋势相同。

在第2 主成分中，DMA（C）的系数最大，其次为SOD（A）；而GSH（B）和TAOC（D）的系数均为负值。因此，第2 主成分反映了当该主成分较大时，DMA 和SOD 的值会增大，GSH 和TAOC 的值会变小。

例10.2　某猪场测定了20 头互助八眉猪后备猪的7 项生长发育指标：2 月龄体重（W2M，kg）、4 月龄体重（W4M，kg）、6 月龄体重（W6M，kg）、6 月龄体长（LEN6M，cm）、6 月龄体高（HEI6M，cm）、6 月龄胸围（CHE6M，cm）和6 月龄管围（CAN6M，cm），数据见表10.2，使用该数据进行主成分分析，并建立用其他性状估计后备猪体重的最优回归方程。

表10.2　20 头互助八眉猪后备猪的7 项生长发育指标数据表

续表

(www.xing528.com)

SAS 程序如图10.6 所示。

图10.6　例10.2SAS 程序图（1）

结果输出为：

1.分析变量的简单统计量（平均数、标准差）

本部分给出了所有7 个变量的平均值和标准差。如W2M 的平均数为17.153 0，标准差为3.208 6。

SAS 程序如图10.7 所示。

图10.7　例10.2SAS 程序图（2）

2.变量间的相关系数矩阵

从各变量间的相关系数可以看出，除了6 月龄管围与2 月龄体重、4 月龄体重、6 月龄体重、6 月龄胸围以及4 月龄体重与6 月龄体高间呈负相关外，其余变量间都为正相关关系，其中以6 月龄体重与6 月龄胸围间的相关程度最高（0.807 2）。

SAS 程序如图10.8 所示。

图10.8　例10.2SAS 程序图（3）

3.相关系数矩阵的特征值、贡献率及累计贡献率

主成分分析结果，前4 个主成分的方差（特征值）分别为2.724 1，1.765 1，1.037 38 和0.701 1；贡献率分别为0.389 2，0.252 2，0.148 2 和0.100 2，累计贡献率达到了0.889 7，表示这4 个主成分包含了原来7 个指标88.97%的信息量。

SAS 程序如图10.9 所示。

图10.9　例10.2SAS 程序图（4）

4.特征向量

根据计算出来的特征向量，可写出由标准化变量所表达的前4 个主成分的关系式：

PRIN1=0.2025W2M +0.4631W4M +0.5549W6M +0.3765LEN6M +0.1879HEI6M +0.4759CHE6M-0.1816CAN6M

PRIN2=0.2312W2M -0.0693W4M -0.1928W6M +0.4804LEN6M +0.5956HEI6M -0.2233CHE6M+0.5187CAN6M

PRIN3= -0.7842W2M +0.2627W4M +0.0379W6M +0.2438LEN6M -0.2066HEI6M +0.0947CHE6M+0.451CAN6M

PRIN4= 0.3659W2M + 0.622W4M - 0.0588W6M + 0.0518LEN6M - 0.4486HEI6M -0.4991CHE6M+0.1503CAN6M

SAS 程序如图10.10 所示。

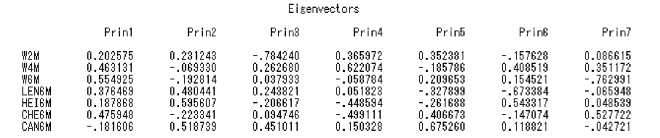
图10.10　例10.2SAS 程序图（5）

5.逐步回归分析（STEPWISE）

本部分结果为采用逐步回归分析方法建立由其他变量估计6 月龄体重的最优方程的输出结果。

W6M= -2.3637 +0.3765W4M+0.5342CHE6M

所估计的回归系数都达到了显著水平（P<0.01），决定系数R2=0.792 0，表明所建立的回归方程具有较高的可靠性。从方程的变量来看，与第1 主成分的意义一致，即4 月龄体重和6 月龄胸围较大的八眉猪，其6 月龄体重也更大。

SAS 程序如图10.11 所示。

图10.11　例10.2SAS 程序图（6）