指标型聚类分析（R型聚类）实例应用

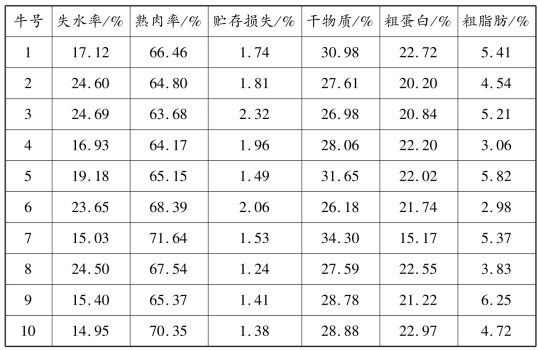
例9.3　测定10 头牦牛的背最长肌常规数据反映牦牛的肉品质，指标有失水率（%）、熟肉率（%）、贮存损失（%）、干物质（%）、粗蛋白（%）和粗脂肪（%）6 项，具体数据见表9.3，试利用该数据进行R 型聚类分析。

表9.3　10 头牦牛的背最长肌常规数据表

SAS 程序如图9.9 所示。

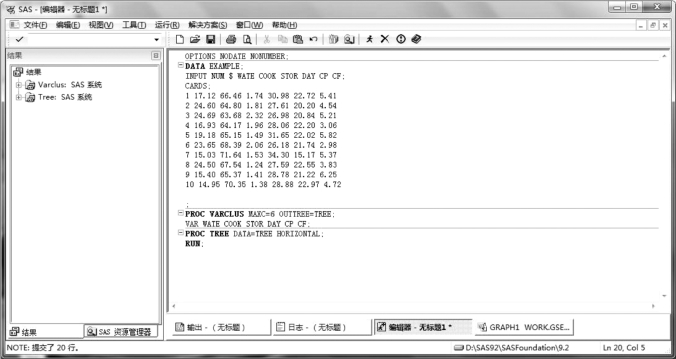
图9.9　例9.3SAS 程序图（1）

输出结果为：

1.聚类分析的具体过程：

①先将所有指标作为1 类。此时总方差6，由类分量所解释的方差为2.874 9，占总方差的0.479 1。第二特征值为1.102 3，大于系统默认的1，因而需要再进行分类。

SAS 程序如图9.10 所示。

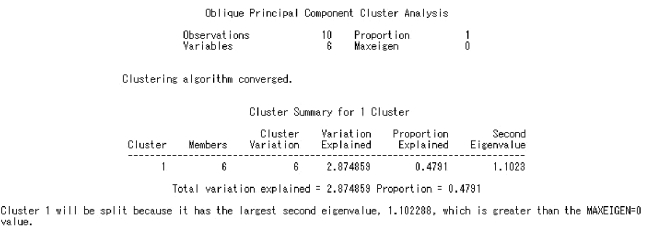
图9.10　例9.3SAS 程序图（2）

②将所有指标分成两类。同样，也计算了每一类的由类分量所解释的方差及其占总方差的比例和第二特征值。所能解释的方差总和为3.819 5，占总方差的比例为0.636 6。

SAS 程序如图9.11 所示。

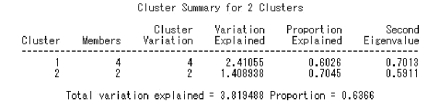
图9.11　例9.3SAS 程序图（3）

本部分列出了两类所包含的变量名，第1 类包括失水率（WATE）、贮存损失率（STOR）、干物质（DAY）、粗脂肪（CF）。其中，第二列为某变量与所在类的相关系数（R2），反映了该变量与同类变量间的相关程度；第三列为某变量与邻近类相关系数，反映了该变量与最相邻类的相关程度，最后一列为1 -R2的比率，其值为（1 -本类R2）/（1 -临类R2），它综合了前两个统计量，该值越小表明分类效果越好。

SAS 程序如图9.12 所示。

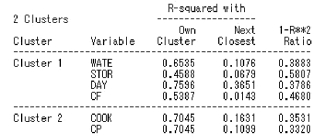
图9.12　例9.3SAS 程序图（4）

本部分标准得分系数、聚类结构及类分量间的相关系数。其中，标准得分系数为第1 类分量和第2 类分量与标准化原始变量间的线性组合系数，即由原始变量预测类分量的标准回归系数；聚类结构则是每个变量与类分量间的相关系数。

SAS 程序如图9.13 所示。

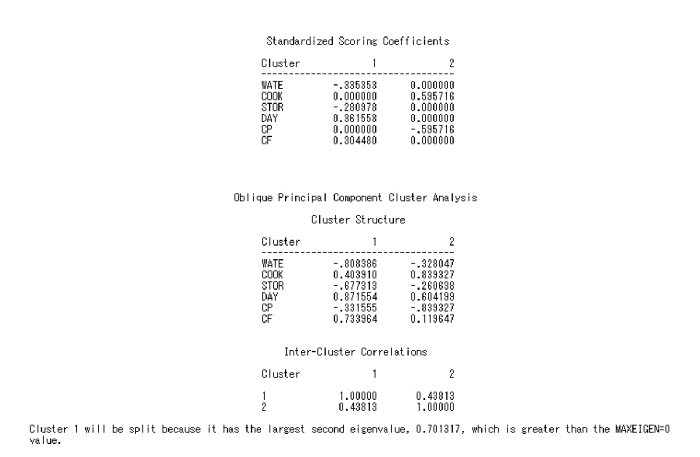
图9.13　例9.3SAS 程序图（5）

③将第2 类分为两类。此时，所有变量分为3 类。所解释的方差总和为4.488 3，占总方差的比例为0.748 1。其中第3 类所解释的方差比例已达到1.000 0，故不再进行分类，而第1、2 两类则需进一步分类。

SAS 程序如图9.14 所示。

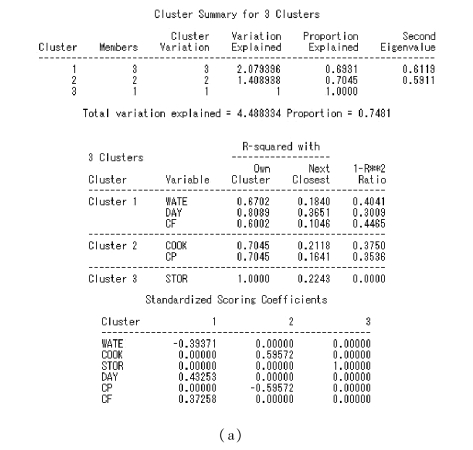
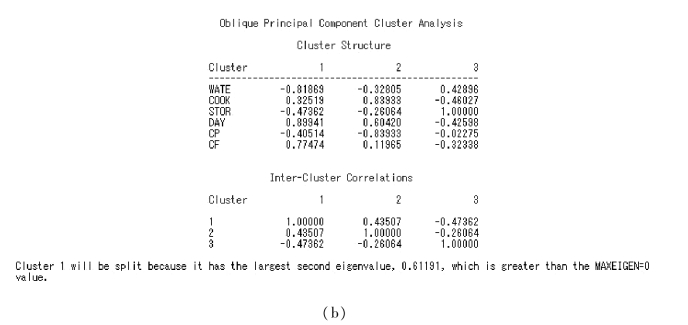
图9.14　例9.3SAS 程序图（6）

④再将第1 类分为两类：此时，所有变量分为4 类。所解释的方差综合为5.053 2，占总方差的比例为0.842 2。其中，第3、4 两类所解释的方差比例都达到了1.000 0，故也无须再进行分类。

SAS 程序如图9.15 所示。

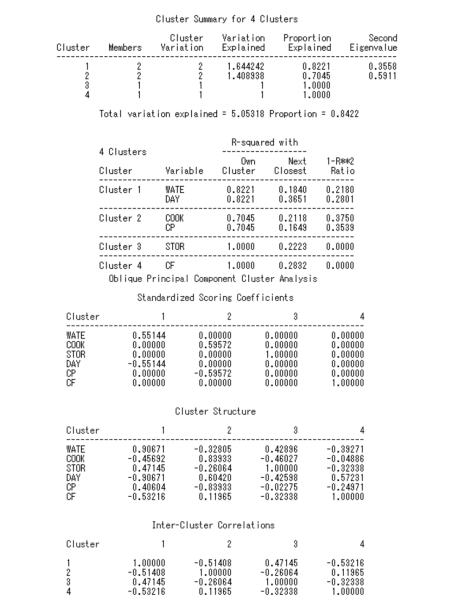
图9.15　例9.3SAS 程序图（7）

⑤再将第1 类分为两类：此时，所有变量分为5 类。所解释的方差总和为5.644 2，占总方差的比例为0.940 7。其中，第2 至5 类所解释的方差比例已达到1.000 0，故无须再进行分类。

SAS 程序如图9.16 所示。

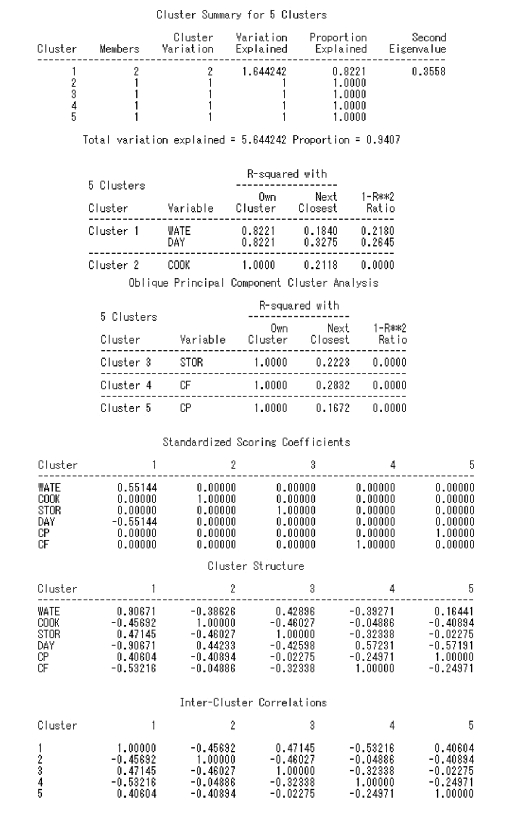
图9.16　例9.3SAS 程序图（8）(www.xing528.com)

⑥继续将第1 类分类两类。此时，所有变量分为6 类，每一类只包含1 个指标。所解释的方差总和为6，占总方差比例为1.000 0。所有6 类所揭示的比例都达到了1，停止分类，给出聚类分析过程的汇总表。其主要包括偏斜主成分聚类分析6 类聚类摘要、相关系数、标准得分系数、偏斜主成分聚类分析聚类结构、类分量间的相关系数、偏斜主成分聚类分析。

SAS 程序如图9.17 所示。

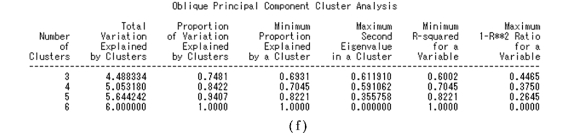
图9.17　例9.3SAS 程序图（9）

2.聚类图

根据聚类图的结果可将6 个肉品质指标分为两类：第1 类包括失水率、干物质、粗脂肪和贮存损失，反映了肌肉的营养品质；第2 类包括熟肉率和粗纤维，反映了肌肉的持水力。

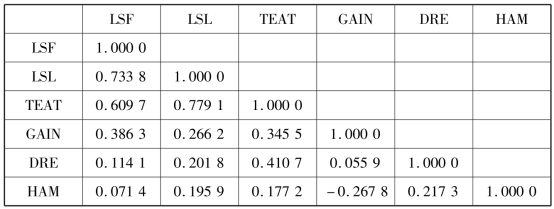
例9.4　已知青海互助八眉猪初产仔猪数（LSF）、经产仔猪数（LSL）、乳头数（TEAT）、日增重（GAIN）、屠宰率（DRE）和腿臀比例（HAM）6 个性状间的相关系数（表9.4），试进行各指标的聚类分析。

表9.4　青海互助八眉猪6 个性状相关系数数据表

SAS 程序如图9.18 所示。

图9.18　例9.4SAS 程序图（1）

输出结果为：

1.聚类分析的具体过程

①先将所有的指标聚类为1 类。此时，总方差为6，由类分量所解释的方差为3.223 0，占总方差比例的0.537 2、第二特征值为1.508 4，大于系统默认的1，需要继续进行分类。

SAS 程序如图9.19 所示。

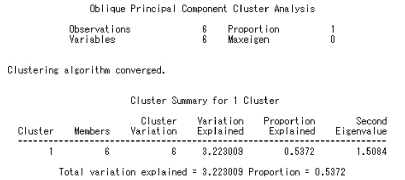
图9.19　例9.4SAS 程序图（2）

②将所有指标分成两类。此时，所解释的方差总和为4.629 7，占总方差比例的0.771 6。

SAS 程序如图9.20 所示。

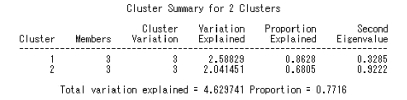
图9.20　例9.4SAS 程序图（3）

以下部分列出了两类所包含的变量名，第1 类包括LSF、LSL 和TEAT，第2 类包括GAIN、DRE 和HAM。同样也计算了相应的统计量。

SAS 程序如图9.21 所示。

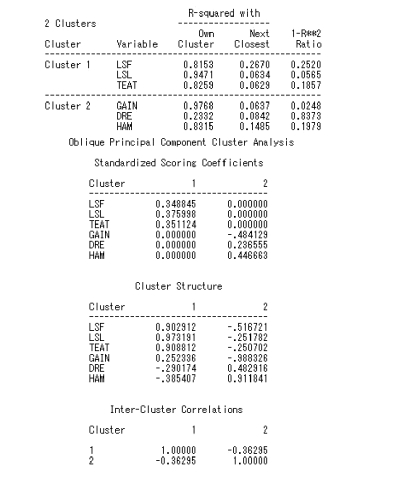
图9.21　例9.4SAS 程序图（4）

③将第2 类进一步分为两类。此时，所有变量共分为3 类。所解释的方差总和为5.498 4，占总方差的比例为0.916 4。由于在程序中规定了最大分类数为3（MAXC=3），因而不再继续分类。

SAS 程序如图9.22 所示。

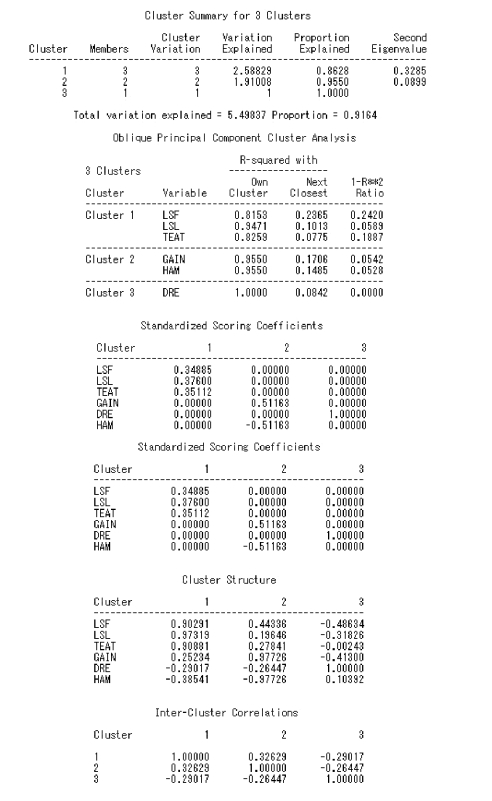
图9.22　例9.4SAS 程序图（5）

2.聚类图

根据聚类图的结构，可将6 个性状分为两类：第1 类包括GAIN、HAM 和DRE 性状，反映了猪的育肥和屠宰性能；第2 类包括LSF、LSL 和TEAT，反映了猪的繁殖性状。

SAS 程序如图9.23 所示。

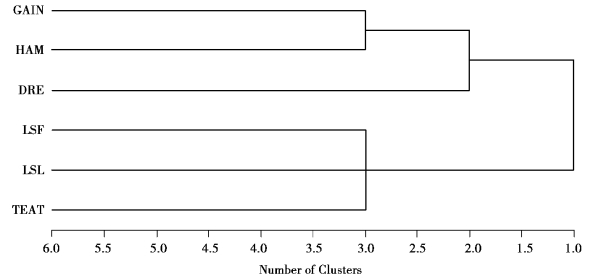
图9.23　例9.4SAS 程序图（6）