例7.1 为了寻找一种较好的哺乳仔猪食欲增进剂,以增加仔猪食欲,提高断奶重,现对哺乳仔猪进行以下试验:试验设对照饲粮和由3 种食欲增进剂配制的饲粮1、饲粮2 和饲粮3共4 个处理,每个处理重复12 次,选择初生重尽量相同的青海互助八眉猪哺乳仔猪48 头,完全随机分为4 组,每组12 头,分别饲喂4 种饲粮。哺乳仔猪初生重x,50 日龄重y 的观测值列于表7.1,试对该资料进行回归模型的协方差分析。
表7.1 试验猪初生重、50 日龄重实验数据列表

SAS 程序如图7.1 所示。
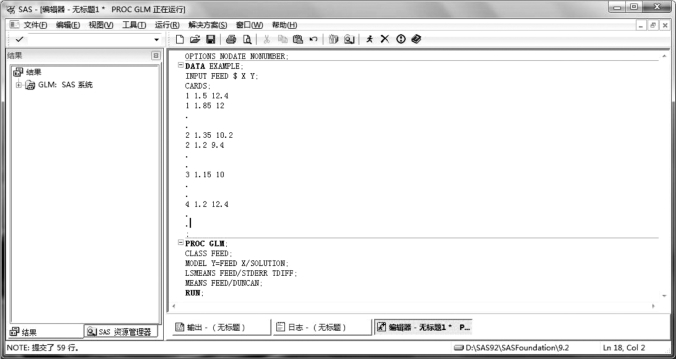
图7.1 试验猪初生重、50 日龄重资料协方差分析SAS 过程
输出结果为:
1.方差分析
该部分输出的内容包括回归模型的显著性检验、处理效应及协变量与因变量回归关系的显著性检验等。
(1)回归模型检验
方差分析结果,F=17.01,P<0.000 1,表明回归模型显著成立。
SAS 程序如图7.2 所示。
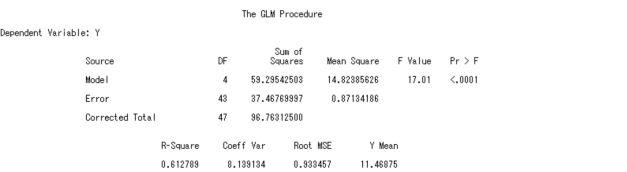
图7.2 例7.1SAS 程序图(1)
(2)处理效应及协变量与因变量回归关系的检验
本部分自动输出Ⅰ型和Ⅲ型平方和,实际应用过程中一般选取Ⅲ型平方和的计算结果。本题中,不同类型的饲料(FEED)对仔猪50 d 体重的影响(F=7.82,P=0.000 3 <0.01),达到了显著水平,表明不同增进剂日粮饲喂的仔猪调整后的断奶体重间有显著性差异;调整后的断奶体重与初生重(X)间呈显著的直线关系(F=54.65,P=0.000 1 <0.01),说明进行协方差分析有实际意义。
SAS 程序如图7.3 所示。

图7.3 例7.1SAS 程序图(2)
2.回归模型的参数估计
该部分输出了回归模型中各参数的估计值及其准确性。本题中,模型的截距(INTERCEPT)为2.840 2(P=0.018 1 <0.05),协变量X 的回归系数为7.199 8(P=0.000 1 <0.01)。调整后的50 日龄体重(Y)与初生重(X)的直线回归方程为:Y=2.840 2 +7.199 8X。
SAS 程序如图7.4 所示。

图7.4 例7.1SAS 程序图(3)
3.最小二乘均数(已校正)及其显著性差异检验
不同增进剂日粮饲喂的哺乳仔猪50 d 体重校正后的均数(最小二乘均数),除了对照组与饲粮1(P=0.106 5 >0.05)、饲粮2 与饲粮3(P=0.691 0 >0.05)的差异不显著外,其余饲粮间的仔猪50 d 体重的差异达到了显著水平(P<0.01);其均数的大小顺序为:饲粮3 >饲粮2 >饲粮1 >对照组。
SAS 程序如图7.5 所示。

图7.5 例7.1SAS 程序图(4)
4.普通均数(未校正)的多重比较
未校正的普通均数间多重比较结果,对照组的仔猪50 d 体重与饲粮2、饲粮3 的差异均不显著(P>0.05),与饲粮1 差异显著(P<0.05);饲粮1 与饲粮2 间的差异显著(P<0.05),其50d 体重均数的大小顺序依次为:饲粮2 >对照组>饲粮3 >饲粮1,与上述校正后的均数及其显著性检验结果不同。
SAS 程序如图7.6 所示。

图7.6 例7.1SAS 程序图(5)
例7.2 用3 种不同比例的精粗比日粮对青海省海南州哇玉香卡农场藏羊进行了2 个批次的育肥试验(育肥期6 个月),育肥初始重和结束重的体重数据列于表7.2,试进行不同饲料和批次对育肥藏羊试验末重影响的协方差分析。
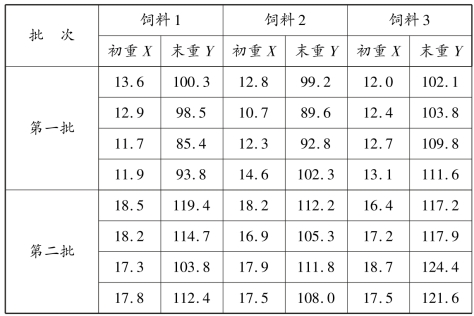
表7.2 藏羊不同饲料和不同批次育肥试验数据表
SAS 程序如图7.7 所示。
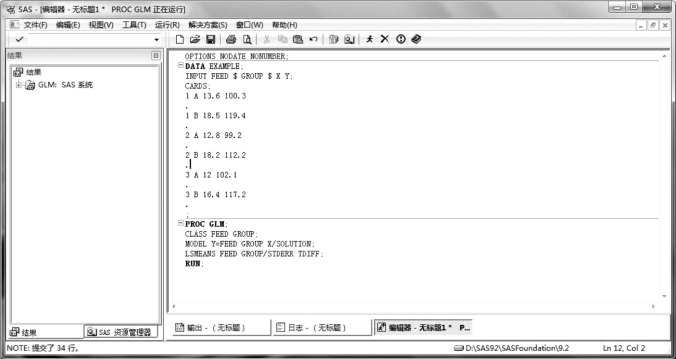
图7.7 藏羊不同饲料和不同批次育肥试验协方差分析SAS 程序
输出结果:
1.方差分析
(1)回归模型的方差分析
F=70.86,P=0.000 1 <0.01,达到了极显著水平。
SAS 程序如图7.8 所示。
(2)处理效应及协变量对因变量影响的显著性检验
方差分析结果表明,不同饲料校正后的末重均数存在显著性差异(F= 41.68,P=0.000 1 <0.01),不同批次末重均数间差异显著(F=6.53,P=0.019 3 <0.05)。调整后的末重均数Y 与初始重X 间呈直线关系。
SAS 程序如图7.9 所示。(https://www.xing528.com)
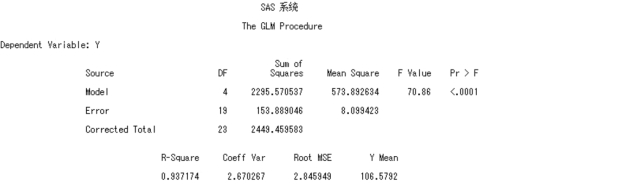
图7.8 例7.2SAS 程序图(1)

图7.9 例7.2SAS 程序图(2)
2.回归模型的参数估计
参数估计结果表明,模型截距(INTERCEPT)为35.740 7(P=0.011 2 <0.05),协变量X的回归系数为4.857 4(P=0.000 1 <0.01),表明X 与因变量Y 存在如下的线性关系:Y=35.740 7 +4.857 4X。
SAS 程序如图7.10 所示。

图7.10 例7.2SAS 程序图(3)
3.最小二乘均数及其显著性检验
(1)不同饲料的最小二乘均数及其显著性检验
3 种饲料的末重的最小二乘均数分别为:102.950 6 g、102.670 2 g 和114.116 7 g,且第1种饲料与第3 种饲料、第2 种饲料与第3 种饲料间差异显著(P<0.01),第1 种饲料和第2 种饲料间差异不显著(P>0.05)。
SAS 程序如图7.11 所示。
(2)不同批次的最小二乘均数及其显著性检验
两个批次末重的最小二乘分别为111.526 9 g 和101.631 4 g,两个批次差异显著(P=0.019 3 <0.05)。
SAS 程序如图7.12 所示。

图7.11 例7.2SAS 程序图(4)

图7.12 例7.2SAS 程序图(5)
例7.3 为比较3 种精饲料对育肥藏羊的增重效果的影响。将24 只藏羊随机分为3 组,每组8 只,分别测量每只藏羊的试验初始年龄(X1)、育肥期采食量(X2)和所增体重(Y)的数据见表7.3,试对比3 种饲料对育肥期增重效果的影响。
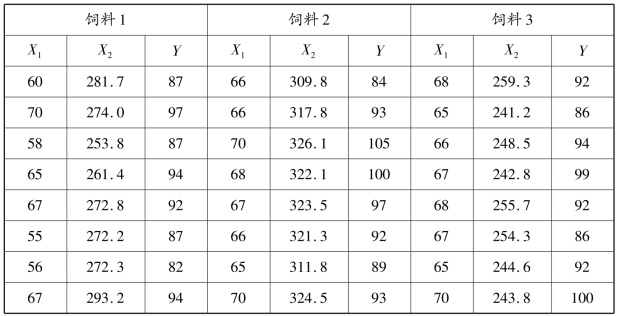
表7.3 藏羊初始年龄、采食量及增重数据表
SAS 程序如图7.13 所示。
输出结果为:
1.方差分析
(1)回归模型检验
对模型的检验结果,F=4.45,P=0.010 5 <0.05,达到了显著水平。
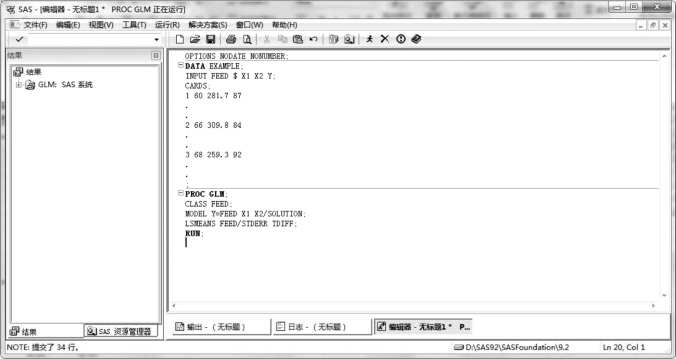
图7.13 藏羊初始年龄、采食量及增重协方差分析SAS 分析
SAS 程序如图7.14 所示。

图7.14 例7.3SAS 程序图(1)
(2)处理效应与协变量对因变量影响的显著性检验
分析结果表明,不同饲料对增重的影响差异不显著(F=0.27,P=0.763 1 >0.05);初始日龄对增重的影响差异极显著(F=12.42,P=0.002 3 <0.01);采食量对增重的影响差异不显著(F=0.00,P=0.982 0 >0.05)。
SAS 程序如图7.15 所示。
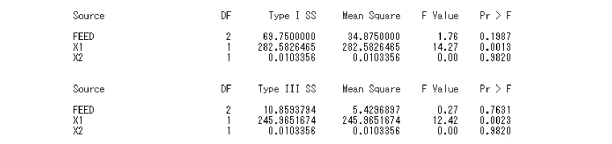
图7.15 例7.3SAS 程序图(2)
2.回归模型参数估计
参数模型估计结果表明,截距(INTERCEPT)为23.931 5(P=0.425 0 >0.05),X1的回归系数为1.015 1(P=0.002 3 <0.01),X2的回归系数为0.002 7(P=0.982 0 >0.05),说明Y与X1和X2间存在如下的线性关系:Y=23.931 5 +1.0151X1+0.002 7X2。
SAS 程序如图7.16 所示。

图7.16 例7.3SAS 程序图(3)
3.最小二乘均数及其显著性检验
3 种饲料的增重最小二乘均数分别为:93.320 1 kg、92.240 7 kg 和91.189 2 kg,彼此间的差异均未达到显著水平(P>0.05),表明3 种饲料对猪增重的影响差异不显著。
SAS 程序如图7.17 所示。

图7.17 例7.3SAS 程序图(4)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




