典型相关分析的作用与实现方法

在动物科学试实际数据分析中，有时还需要描述两组变量之间的相关性，例如畜禽生长发育性状与繁殖性状之间、某些数量性状与某些环境因素之间的相关性等。第二节相关分析方法就无法解决此类问题，而必须引入一种新的相关分析方法——典型相关分析（canonical correlations analysis）。

典型相关分析是研究描述观察对象的两组指标（变量）之间相关性的一种统计分析方法，如在动物生产中，大通牦牛的体型可以用体高、体长、胸围、胸宽、腹围、管围等体尺指标来描述，生长速度可以用某一月龄的体重、某一阶段的增长速率来描述，因而，研究大通牦牛体型和生长速度两方面特性的关系就可以归结为研究这两个指标相关性的问题，此时就需要采用典型相关分析来进行。对于两组多个指标，不仅两组指标间具有相关性，而且同一组内的不同指标间也有一定的相关性。组间和组内指标间的相关关系较为复杂，因此用简单相关分析系数和复相关分析系数很难全面真实反映两组指标之间的关系。典型相关分析就是将两组的多个指标分别线性组合为少数几对典型变量（canonical variable），并用典型相关系数（canonical correlation coefficient）来描述每对典型变量间的相关关系。

（一）CANCORR 过程

在SAS 统计分析系统中，典型相关分析是通过CANCORR 过程来完成的。

PROC CANCORR 选项列表；

VAR 变量名列表；

WITH 变量名列表；

PARTIAL 变量名列表；

FREQ 变量名；

WEIGHT 变量名；

上述语句中，通常只有VAR 和WITH 语句经常同PROC CANCORR 语句一起使用，且WITH 语句是必需的，其余语句都是可选择性语句。

（二）语句说明

1.PROC CANCORR 语句

该语句调用CANCORR 过程进行典型相关分析，主要选项有：

（1）数据集选项

DATA=输入数据集，用于指定分析数据集，如果省略该选项，则对最近创建的数据集进行分析；OUT=输出数据集，储存所有的原始数据和典型相关变量得分；OUT -STAT=输出数据集，储存典型相关系数统计量。

（2）结果输出选项

ALL 所有输出项；NOPRINT 不输出分析结果；SHORT 只输出典型相关系数和多元分析统计数；SIMPLE 简单统计量（平均数和标准差）；CORR 相关系数等。VNAME=“标签”，规定VAR 语句中的变量标签，缺省时为VAR 变量；VPREFIX=前缀名，规定来自VAR 语句的典型变量名的前缀；WNAME= “标签”，规定WITH 语句中的变量标签，缺省时为WITH 变量；WPREFIX=前缀名，规定来自WITH 语句的典型变量名的前缀，要求与VPREFIX 相同。

（3）多元回归选项

VDEP|WREG，规定用VAR 变量作为因变量，而WITH 变量作为回归变量进行多元回归分析；WDEP|VREG，规定以WITH 变量作为因变量，而VAR 变量作为自变量进行多元回归分析。以下选项则只有在规定结果输出的选项不为ALL 时才起作用，其中NOINT 规定模型中不包含回归截距；STB 为标准偏回归系数；T 为对回归系数进行t 检验。

2.VAR 语句

列出被分析的两组变量中的第一组变量。这些变量必须都是数值型变量。如果省略VAR 语句，则在其他语句中没有提到的所有数据型变量组成第一组变量。

3.WITH 语句

WITH 语句是一个必须语句，用于列出被分析的两组变量中的第二组变量，这些变量必须是数值型变量。

4.PARTIAL 语句

该语句用于给出当用户希望基于偏相关矩阵进行典型相关分析。

5.FREQ 语句

该语句用于给出说明如果输入数据集中有一个变量的值表示观测中其他值出现的频数的变量名。

6.WEIGHT 语句

该语句用于给出如果用户想计算加权乘积矩阵相关系数的加权数变量名。

（三）结果输出

在不对输出结果做特殊规定的情况下，CANCORR 过程会输出每个分析变量的平均数和标准差，变量间的相关系数、典型相关系数及校正的典型相关系数以及这些典型相关系数的渐进标准误、典型相关系数的平方、特征值及其贡献率、典型相关系数的显著性检验结果，典型变量与原始变量间的相关系数及典型冗余分析等。

（四）典型相关系数计算的示例应用

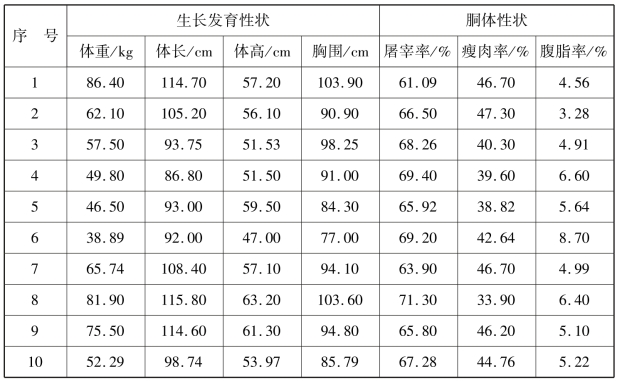
检测中国10 个地方品种猪的生长发育性状指标和胴体性状指标共7 项指标，其中生长发育性状包括体重、体长、体高和胸围4 项指标，胴体性状包括屠宰率、瘦肉率和腹脂率3 项指标，具体数据见表6.12，试进行典型相关分析。

表6.12　猪生长发育性状和胴体性状数据表

SAS 程序如图6.42 所示。

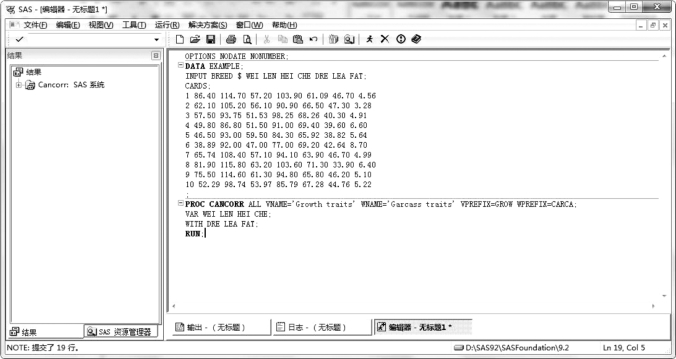
图6.42　猪生长发育性状和胴体性状典型相关分析SAS 程序

输出结果为：

1.分析变量的简单统计量

在该部分中，系统会计算出每个分析变量的平均数（Means）和标准差（Std Dev）。如本例中体重（WEI）的平均数为61.662，标准差为15.720 374。

SAS 程序如图6.43 所示。

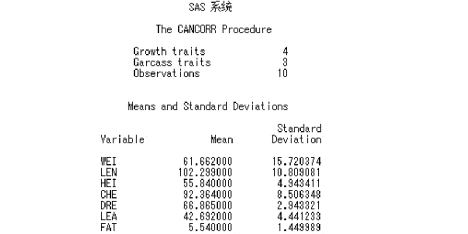
图6.43　简单统计量SAS 程序图

2.分析变量间的相关系数

计算出所有分析变量间的简单相关系数（Correlations）。如本例中体重（WEI）与体长（LEN）间的简单相关系数为0.918 5，屠宰率（DRE）与瘦肉率（LEA）间的相关系数为-0.732 9，体重（WEI）与屠宰率（DRE）间的相关系数为-0.381 1。

SAS 程序如图6.44 所示。

图6.44　相关系数SAS 程序图

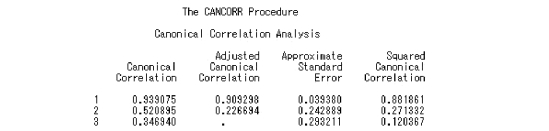
3.两组变量间的典型相关系数

计算出分析的两组变量间的n 个典型相关系数（Canonical Correlation）及其近似标准误（Approx Standard Error）等。本例中生长发育性状与胴体性状间的第1 典型相关系数r1=0.939 075，第2 典型相关系数为r2=0.520 895，第3 典型相关系数为r3=0.346 940；第1 到第3 个典型相关系数的近似标准为分别为0.039 380、0.242 889 和0.293 211。

SAS 程序如图6.45 所示。

(www.xing528.com)

图6.45　典型相关系数SAS 程序图

4.特征值及其贡献率

计算出n 个特征值λ 及其贡献率。本例中，第1 个到第3 个特征值（Eigenvalue）分别为7.464 6、0.372 4 和0.136 8，贡献率（Proportion）分别为0.936 1、0.046 7 和0.017 2，前两个特征值的累积贡献率（Cumulative）为0.982 8。

5.典型相关系数的显著性检验

对所计算的典型相关系数进行显著性检验。在进行实际数据分析时，根据第一部分计算的结果即可作出判断。检验结果，第1 到第3 典型相关系数的P 值分别为0.440 7、0.901 9和0.725 7（P>0.05），差异均不显著。

SAS 程序如图6.46 所示。

图6.46　显著性检验SAS 程序图

6.典型变量中原指标的典型系数

本部分用实际测量指标（变量）来线性表达典型变量的系数。本例中，生长发育性状：

第1 典型变量GROW1=0.092 9WEI+0.028 4LEN-0.202 9HEI-0.185 2CHE

第2 典型变量GROW2= -0.330 9WEI+0.212 8LEN+0.002HEI+0.301CHE

第3 典型变量GROW3= -0.357 6WEI+0.394 6LEN-0.117 6HEI+0.339 3CHE

胴体性状：

第1 典型变量CARCA1=0.108 9DRE+0.276 8LEA+0.560 9FAT

第2 典型变量CARCA2=0.406 9DRE+0.062 1LEA+0.177 9FAT

第3 典型变量CARCA3=0.319 2DRE-0.017 7LEA-0.624 6FAT

SAS 程序如图6.47 所示。

图6.47　典型系数SAS 程序图（1）

以下为采用标准化的指标来线性表达典型变量，其中，

生长发育性状：

第1 典型变量GROW1=1.460 9WEI+0.306 5LEN-1.003 4HEI-1.575 4CHE

第2 典型变量GROW2= -5.203 2WEI+2.299 7LEN+0.009 9HEI+2.560 5CHE

第3 典型变量GROW3= -5.621 9WEI+4.265 7LEN-0.581 5HEI+2.886 1CHE

胴体性状：

第1 典型变量CARCA1=0.320 5DRE+1.229 4LEA+0.813 3FAT

第2 典型变量CARCA2=1.197 9DRE+0.275 9LEA-0.025 7FAT

第3 典型变量CARCA3=0.939 6DRE+0.790 2LEA-0.905 6FAT

SAS 程序如图6.48 所示。

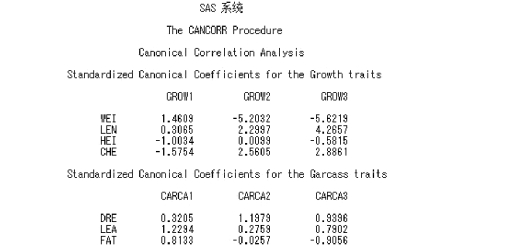
图6.48　典型系数SAS 程序图（2）

7.典型结构

本部分给出的是典型变量与实测值（原始值）变量间的相关系数，包括4 种典型结构矩阵，即两组实测值变量与其本组典型变量和相对组（另一组）典型变量间的相关系数。本例中为生长发育性状实测值变量与其典型变量间的相关、胴体性状实测值变量与其典型变量间的相关、生长发育性状实测值变量与胴体性状典型变量间的相关以及胴体性状实测值变量与生长发育性状典型变量间的相关。

SAS 程序如图6.49、图6.50 所示。

图6.49　典型结构SAS 程序图（1）

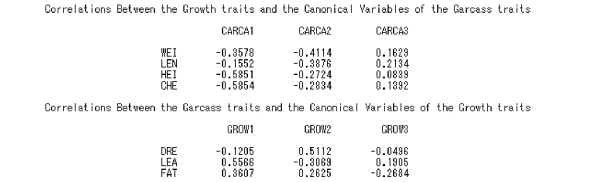
图6.50　典型结构SAS 程序图（2）

8.典型冗余分析

计算典型变量对实测值变量的贡献率，以及实测值变量中的总变异由典型变量解释的比例，包括原实测值变量和标准化的实测值变量与典型变量的结果。在实际分析中，通常取标准化实测值变量的结果。

本例中，生长发育性状第1 到第3 典型变量对实测值变量体重（WEI）、体长（LEN）、体高（HEI）和胸围（CHE）的贡献率（标准化结果）分别为0.237 3、0.436 6 和0.204 5；胴体性状第1 到第3 典型变量对实测值变量体重（WEI）、体长（LEN）、体高（HEI）和胸围（CHE）的贡献率（标准化结果）分别为0.209 3、0.118 5 和0.024 6；胴体性状第1 到第3 典型变量对实测值变量屠宰率（DRE）、瘦肉率（LEA）和腹脂率（FAT）的贡献率（标准化结果）分别为0.171 8、0.521 4和0.306 8；生长发育性状第1 到第3 典型变量对实测值变量屠宰率（DRE）、瘦肉率（LEA）和腹脂率（FAT）的贡献率（标准化结果）分别为0.151 5、0.1415 和0.036 9。

SAS 程序如图6.51、图6.52 所示。

9.复相关系数的平方

该部分输出每个变量同相对变量组中前n 个典型变量复相关系数的平方，它反映的是某一典型变量相对变量组中每个变量的预测能力（其中n 可从1 到典型变量的个数），相应的复相关系数平方的值越大，则预测能力越高。

根据复相关系数的平方可以看出，胴体性状第1 典型变量对体长指标的预测能力较差（复相关系数的平方为0.024 1），对体重、体高和胸围的预测能力稍微高一点（复相关系数的平方分别为0.128 0、0.342 3 和0.342 7）；生长发育性状第1 典型变量对屠宰率（DRE）的预测能力较差（复相关系数的平方为0.014 5），对瘦肉率（LEA）和腹脂率（FAT）的预测能力稍微高一点（复相关系数的平方分别为0.309 8 和0.130 1）。

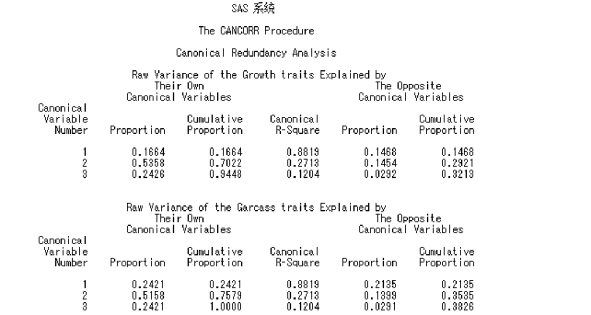
图6.51　典型冗余分析SAS 程序图（1）

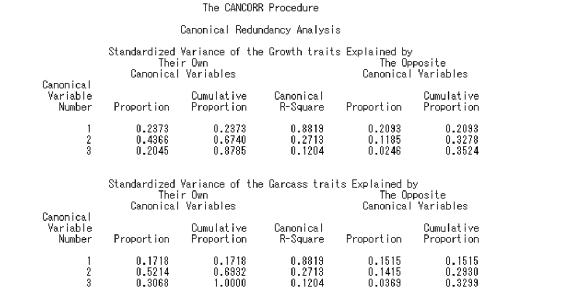
图6.52　典型冗余分析SAS 程序图（2）

SAS 程序如图6.53 所示。

图6.53　典型冗余分析SAS 程序图（3）