SAS统计分析：曲线回归分析

在动物科学试验中，试验动物的两个指标或性状之间的关系大多数不是直线关系，而是曲线关系。例如，畜禽在生长发育过程中的各类生理指标与年龄的关系；奶牛的泌乳量与泌乳天数的关系；细菌的繁殖速度与温度湿度的关系等。虽然在自变量X 的某一取值范围内，因变量Y 与自变量X 之间的关系是直线关系，但就自变量X 可能取值的整个范围而言，因变量Y 与自变量X 之间的关系通常不是直线关系而是曲线关系，因而，进行动物科学试验研究常常需要进行曲线回归分析（curvilinear regression analysis）。

曲线回归分析的基本任务是通过自变量X 与因变量Y 的n 对实际观察值，建立Y 与X 之间的回归方程，通常有两种方法：①利用相关专业知识，确定回归方程，如细菌数量的增长通常符合指数函数的形式y=aebx，仔畜的体重增长通常符合S 形曲线形式，即Logistic 曲线；②另一种是没有现成的实践经验指导，需要作出散点图，观察散点图的时间分布趋势，选用与散点图实测点分布趋势最接近的函数来拟合实测点，用来拟合的函数种类很多，其中许多曲线函数可以通过变量转换转化为直线函数，这种曲线函数称为可直线化的曲线函数。

（一）非线性模型

1.非线性模型

非线性模型（non-linear model）是相对于线性模型而言的，其自变量X 与因变量Y 之间不能在坐标空间表示为线性对应的关系，通常也将这种变量间的关系称为曲线回归。与线性模型不同，非线性模型各偏导数并非都是常数。其一般形式为：

Y=f(x,β)+ε

其中，f（x，β）为某种形式的函数，根据不同的情况而异。从广义的角度来看，线性模型仅是非线性模型的一种特殊形式，它最简单，也最有用，应用范围最广。由于生物体的复杂性，并且受到许多外界环境的影响，因此在很多情况下各种变量之间大量存在的非线性关系。

2.非线性模型的建立和参数估计

（1）非线性模型的建立

非线性模型的特点决定了其形式的多样性，不同的变量间，甚至是相同的变量在不同的实验环境中都有不同的线性关系。因此进行变量间非线性关系分析的关键就是建立一个合适的非线性模型。通常非线性模型的建立主要有两种方法，即推理建模和经验建模。

（2）非线性模型的差数估计

当建立或选择了某种非线性模型后，对非线性为题的处理转化成了确定模型中各参数的问题。其参数的估计主要有两种类型：线性化后的最小二乘法和直接法。

（二）非线性回归分析的SAS 过程

1.调用格式

NLIN 过程的调用格式为：

PROC NLIN 选项；

MODEL 因变量=模型表达式；

PARMS 参数=初始值；

DER.参数[.参数]=偏导表达式；

2.语句说明

（1）PROC NLIN 语句

该语句调用NLIN 过程进行非线性回归分析。其选项主要包括：

①METHOD=循环迭代方法。用于选择非线性回归的具体分析方法。循环迭代方法有GAUSS、MARQUARDT、NEWTON、GRADIENT 和DUD 法。

②SMETHOD=步长。用于确定迭代过程中的步长，包括HALVE、GOLDEN、ARMGOLD和CUBIC 法。

（2）MODEL 语句

用于定义非线性回归模型，可直接给出非线性回归方程的表达式。

（3）PARMS 语句

用于设定参数的初始值。参数初始值的设定有时会对计算结果产生很大的影响，当迭代不能收敛时，可以尝试设定不同的初始值进行重新运算。

（4）DER 语句

给出非线性回归方程对参数的一阶或二阶偏导，当METHOD=DUD 时不需要给出，当METHOD=GAUSS 时，必须给出一阶或二阶偏导。

3.结果输出

NLIN 过程执行后，其输出结果包括循环迭代过程、非线性最小二乘拟合的回归平方和与残差（离回归）平方和、模型参数的估计值及其标准误记忆参数估计值的置信区间和参数估计值间的渐进相关系数等。

（三）非线性模型回归分析应用示例

求解非线性回归模型参数的方法有两大类，一是将非线性回归经线性化的转换后再估计出相应的参数，此时可以用直线回归分析REG 过程或者GLM 过程进行相关参数的估计；二是直接应用NLIN 过程进行分析，这一方法适用于所有的线性回归分析。

例6.5　黑龙江雌性鲟鱼的体长（cm）和体重（kg）8 对观测值列于表6.8 中，对鲟鱼体重和体长进行曲线回归分析，试分析体重和体长是否符合模型Y=（a+b×X）/X。

表6.8　黑龙江雌性鲟鱼体长和体重数据表

SAS 程序如图6.27 所示。

输出结果为：

采用GAUSS-NOWTON 进行迭代求解，经10 次迭代后，误差平方和的变化满足收敛标准，停止迭代。结果得到a= -2 524.1，b=33.067 9，相应的残差平方和为98.737 8。根据此建立的非线性回归方程为：

Y=( -2 524.1 +33.067 9X)/X

相关指数R2=1 -SSE/SSCT=1 -98.737 8/409.1=0.758 6，表明所建立的回归方程拟合度较低，即该回归方程估测的有一定的可靠度但是可靠度不高。

图6.27　黑龙江雌性鲟鱼体长和体重非线性回归SAS 程序

SAS 程序如图6.28—图6.30 所示。

图6.28　例6.5SAS 程序图（1）

图6.29　例6.5SAS 程序图（2）

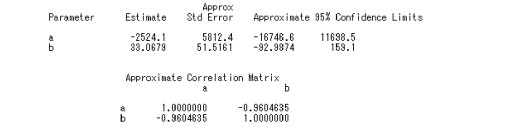
图6.30　例6.5SAS 程序图（3）

（四）动物科学重常用得非线性模型应用示例

1.泌乳曲线

母畜自产羔（产犊、产仔）开始泌乳，其产奶量随着时间的推移呈规律性的变化，具体表现为：泌乳初期产奶量迅速增加，经一定时间后达到泌乳最高峰，然后逐渐下降，直至干乳。当以时间为横坐标，产奶量为纵坐标来描述这种变化过程时，即构成了泌乳曲线（milking curve）。其数学模型为y=axbe -cx，其中，y 为产奶量，x 为时间，a、b、c 为相应的参数（均为正值），其中a 反映了母畜的产奶潜力，b 反映了产奶量上升至最高峰的速率，c 反映了产奶量达到顶峰后下降的速率。(www.xing528.com)

例6.6　为了研究某品种奶牛泌乳期产奶量的变化规律，测定并记录了10 个月的产奶量见表6.9，试进行回归分析。

表6.9　产奶量变化规律

SAS 程序如图6.31 所示。

图6.31　泌乳曲线SAS 程序

输出结果为：

采用GAUSS-NEWTON 法进行迭代求解，经6 次迭代后，误差平方和的变化满足收敛标准，停止迭代。结果得到a=1 301.0，b=0.422 1，c=0.133 8，相应的残差平方和为32 287.0。据此建立的非线性回归方程为：

相关指数R2=1 -32 287/14 451 000=0.997 8，表明所建立的回归方程拟合度较高，即该回归方程估测的可靠度较高。

SAS 程序如图6.32—图6.34 所示。

图6.32　例6.6SAS 程序图（1）

图6.33　例6.6SAS 程序图（2）

图6.34　例6.6SAS 程序图（3）

2.生长曲线

随着日龄的增长，动物体尺体重或某部分会随之发生规律性变化。如果以时间为横坐标，以体尺体重（或身体某部分）作为纵坐标，所得的曲线一般表现为S 形曲线，这就是描述动物生长规律的生长曲线（growth curve）。它反映了生物整体或个体各组成部分生长成熟的内在动力与这种动力进行表达时所处的环境之间的终身相互关系。除此之外，利用生长曲线的参数，还可以预测生长速度、饲料需要量以及选择反应等，通过配合生长曲线分析，还可以比较不同选种方法对生长速度的选择效果，从而提高选种的效果和效率。描述动物生长过程较为常用的模型为Logistic 模型， 以体重随时间的生长曲线为例， 其一般形式为：y=a/（1 +e -k（x-b）），其中，y 为时间为x 时的体重，参数a 表示体重极限，k 为接近这一极限的速率，b 为达到最大生长率的时间，当x=b 时，体重y=a/2，生长曲线达到拐点。

例6.7　肉用四川白鹅的日龄（d）与体重（g）8 对观测值见表6.10，对肉用四川白鹅的体重与日龄进行曲线回归分析。

表6.10　肉用四川白鹅的体重与日龄数据表

SAS 程序如图6.35 所示。

图6.35　肉用四川白鹅的体重与日龄生长规律SAS 程序

输出结果为：

采用试位法（DUD）进行迭代求解，经6 次迭代后，误差平方和的变化满足收敛标准，停止迭代。结果得到a=4 773.6，b=61.175 7，k=0.052 5，相应的残差平方和为4 299.2，P <0.000 1，有极显著的意义。据此建立的非线性回归方程为：

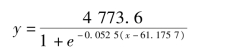
相关指数R2=1 -4 299.2/15 513 446=0.999 7，表明所建立的回归方程拟合度很高，该回归方程估测的可靠程度达到了很高水平。

SAS 程序如图6.36、图6.37 所示。

图6.36　例6.7SAS 程序图（1）

图6.37　例6.7SAS 程序图（2）

3.产蛋曲线

当人们从动态角度考察某一群家禽的平均产蛋量时，会发现其在整个产蛋周期内呈现规律性的变化。在其他条件不变的情况下，当全群进入产蛋期后，产蛋量经过一个短暂的缓慢上升后会迅速增加，达到产蛋顶峰后又逐渐下降，直到产蛋结束。当用时间作为横坐标，以产蛋量作为纵坐标来描述这种变化时就构成了产蛋曲线（egg-laying curve）。1987 年我国学者杨宁在总结以前研究成果的基础上提出产蛋曲线模型，其一般形式为：y= （ae -bx）/（1 +e -c（x-d）），其中y 为对应时间为x 的产蛋量，x 为产蛋时间，参数a 表示群体的最大产蛋潜力，b 反映群体产蛋能力的衰减速率，c 反映开产日龄的变异情况，d 为开产日龄平均数的指示参数。应用产蛋曲线模型，可以对整个产蛋过程的动态变化进行相对精确的描述，同时还可以根据产蛋曲线的规律性变化，对整个产蛋期及全年产蛋量进行较为准确的预测。

例6.8　为研究某品种蛋鸡在产蛋年度中产蛋量的变化规律，记录了12 个产蛋月的平均产蛋量，具体数据见表6.11，试进行回归分析。

表6.11　某品种蛋鸡12 个月平均产蛋量数据表

SAS 程序如图6.38 所示。

输出结果为：

采用试位法（DUD）进行迭代求解，经9 次迭代后，误差平方和的变化满足收敛标准，停止迭代。结果得到a=132.0，b=0.199 6，c=0.522 0，d=4.779 0，相应的残差平方和为1.777 1，P<0.000 1，有极显著的意义。据此建立的非线性回归方程为：

图6.38　某品种蛋鸡产蛋量变化规律的SAS 程序

相应相关指数R2=1 -1.777 1/4 924=0.999 6，表明所建立的回归方程拟合度很高，该回归方程估测的可靠程度达到了很高水平。

SAS 程序如图6.39—图6.41 所示。

图6.39　例6.8SAS 程序图（1）

图6.40　例6.8SAS 程序图（2）

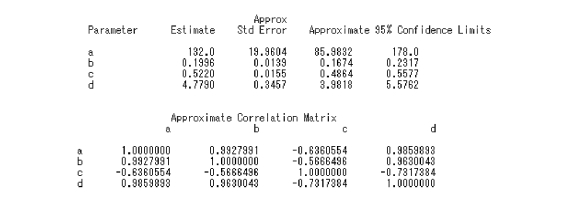
图6.41　例6.8SAS 程序图（3）