在动物科学研究中,人们对变量的相互关系进行分析,当一个变量增大或减少时,另一个变量也会相应地随之增大或减少(或相反趋势),且这种增大或减少在一定范围内呈现一定的比例,则这种增大或减少在一定范围内呈现一定的比例,则表示两个变量间存在着线性相关的关系。两个线性相关的变量之间的性质和密切程度,通常用相关系数(correlation coefficient,r)的正负及大小来衡量。因此,线性相关分析的主要工作就是计算出变量间的相关系数并对其显著性进行检验。简言之,所谓相关分析,就是用一个指标来表明现象间相互依存关系的密切程度。
设有两个变量X 和Y,变量Y 随着变量X 一起变化,并完全依赖于X。当变量X 取某个数值时,Y 根据确定的关系取相应的值,则称Y 是X 的函数,记为Y=f(X),其中X 称为自变量,Y 称为因变量。各观测点落在一条线上。自变量取值一定时,因变量的取值带有一定随机性的两个变量之间的关系称为相关关系。当一个或几个相互联系的变量取一定数值时,与之相对应的另一变量的值虽然不确定,但它仍按某种规律在一定的范围内变化,变量间的这种相互关系,称为具有不确定性的相关关系。
与函数关系不同,相关变量的关系不能用函数关系来精确表达,一个变量的取值不能由另一个变量唯一确定。当变量X 取某个值时,变量Y 的取值可能有无数个,各个观测点分布在直线周围。按照相关程度划分,可分为完全相关、不完全相关和不相关;按相关方向划分,可分为正相关和负相关;按相关的形式划分,可分为线性相关和非线性相关;按变量多少划分,可分为单相关、负相关和偏相关。
在统计学中采用相关分析研究呈平行关系的相关变量间的关系。对两个变量间的直线关系进行相关分析,称为简单相关分析(simple correlation analysis),而对于多个变量进行相关分析时,研究一个变量与多个变量间的线性相关,则称为多元相关分析或复相关分析(multiple correlation analysis);研究其余变量保持不变的情况下两个变量间的线性相关,又称为偏相关分析(partial correlation analysis)。
(一)CORR 过程
1.调用格式
PROC CORR <选项列表>;
BY <DESCENDING>变量名-1 <…< DESCENDING>变量名n> <NOTSORTED>;
FREQ 变量名;
VAR 变量名列表;
WITH 变量名列表;
PARTIAL 变量名列表;
WEIGHT 变量名;
2.语句说明
(1)PROC CORR 语句
用于调用CORR 过程进行相关分析。其常用的选项主要有:
①PEARSON。计算通常的pearson 相关系数,即直线相关系数,缺省时系统会默认计算出该相关系数。
②SPEARMAN。计算Spearman 等级相关系数(或秩相关系数)。
③NOSIMPLE。取消打印每个变量的描述性统计量(如平均数、标准差等)。如果该项缺省,则会打印出每个分析变量的基本统计量。
(2)VAR 语句
用于指明所要分析的变量,如果缺省,则系统默认对其他语句中没有提及的所有数值型变量进行分析。
(3)WITH 语句
用于设定放在左边的变量,与VAR 语句配合使用,此时VAR 语句的变量间和WITH 语句的变量间的相关系数不给出,只输出VAR 变量和WITH 变量间的相关系数。如果该语句缺省,则系统会计算VAR 语句中的所有变量之间的两两相关系数。
(4)PARTAIL 语句
在进行偏相关分析时,用于指明偏相关变量(即相对固定的那些变量)。需要注意的是,PARTAIL 语句指定的变量名不能出现在VAR 和WITH 语句中。
3.结果输出
CORR(表6.4)过程执行后,其输出的结果包括简单统计量、相关系数及其显著性检验。在设定PARTAIL 变量时,还可进行偏相关分析。
表6.4 PROC CORR 语句选项列表及其功能

续表

(二)简单相关系数计算的示例应用
所谓的简单相关分析,又称直线相关分析或一元相关分析,就是只涉及一对(两个)变量的相关关系的分析。
例6.4 10 只绵羊的胸围(cm)与体重(kg)的观测值见表6.5,计算绵羊的胸围与体重的相关系数。
表6.5 10 只绵羊的胸围与体重数据表

试进行两个性状的相关分析。
SAS 程序如图6.19 所示。

图6.19 10 只绵羊的胸围与体重SAS 程序
输出结果为:
1.分析变量的基本统计量
该部分输出了所有分析变量的平均数和标准差等基本统计量。本例中,胸围(X)和体重(Y)的平均数(Mean)分别为72.000 0 cm 和68.000 0 kg,标准差(Std Dev)分别为2.666 7 和8.013 88。
SAS 程序如图6.20 所示。(https://www.xing528.com)

图6.20 例6.4SAS 程序图(1)
2.相关系数及其显著性检验
该部分输出所分析的相关变量间的简单相关系数,以及在假设r=0 前提下相应的概率,对所计算的相关系数进行显著性检验。本例中,胸围与体重间的相关系数为0.847 49,P=0.002 0 <0.01,差异极显著,说明胸围与体重呈现极显著相关关系。
SAS 程序如图6.21 所示。

图6.21 例6.4SAS 程序图(2)
(三)偏相关系数计算的示例应用
当对多个变量的相关性进行分析时,仅根据两个变量间的简单相关系数往往不能很好地说明彼此间的真正关系,只有在去除其他变量影响的情况下,计算出它们之间的相关系数,才能真正解释它们之间的相关关系。在多个相关变量中,其他变量保持固定不变,所研究的两个变量间的线性相关就称为偏相关(partial correlation)。这样计算出来的相关系数就称为偏相关系数(partial correlation coefficient)或净相关系数,它是表示两个变量偏相关的性质和程度的统计量,相应的分析就称为偏相关分析。
某屠宰场测定10 头猪的宰前体重(WEI,kg)、屠宰率(DRE,%)、背膘厚(BF,cm)、眼肌面积(LA,cm2)和胴体瘦肉率(LEAN,%)5 项育肥胴体指标,数据见表6.6,是做固定宰前体重和屠宰率时,胴体瘦肉率与背膘厚、眼肌面积间的偏相关分析。
表6.6 猪5 项育肥胴体指标数据表

续表

SAS 程序如图6.22 所示。

图6.22 偏相关分析SAS 程序
输出结果为:
1.简单相关系数
该部分输出的是所有5 项指标两两之间的简单相关系数。其中WEI 和LEAN 相关系数为0.668 02(P=0.034 8 <0.05)、BF 和LA 相关系数为0.772 84(P=0.008 8 <0.01)、BF 和LEAN 相关系数为0.822 72(P=0.003 5 <0.01)、LA 和LEAN 相关系数为0.963 59(P <0.000 1),两两之间存在显著的相关性。
SAS 程序如图6.23 所示。
2.固定宰前体重(WEI)和屠宰率(DRE)时的偏相关分析
当固定宰前体重(WEI)和屠宰率(DRE)、瘦肉率(LEAN)与背膘厚度(BF)和眼肌面积(LA)的偏相关系数分别为-0.844 95 和0.941 26 时,都达到了极显著水平(P <0.01),也与简单相关系数的大小明显不同。偏相关分析的结果表明,胴体瘦肉率与背膘厚间呈较强的负相关,而与眼肌面积则为较强的正相关。
SAS 程序如图6.24 所示。
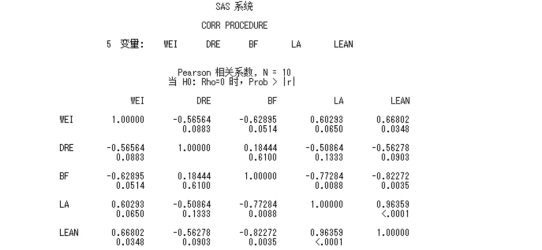
图6.23 例6.4SAS 程序图(3)

图6.24 例6.4SAS 程序图(4)
(四)等级相关分析计算的示例应用
等级相关(rank correlation),又称为秩相关,是研究两个变量之间大小次序的相关分析,属于非参数分析的范畴。在相关分析中,要求所分析的两个变量均服从正态分布。若不满足这一条件,要定量地描述两变量的协同变化,可计算其等级相关系数。在动物科学研究中,畜禽的个体遗传评定,通过不同的遗传评定方法育种值估计的准确性就可以通过估计育种值与真实值之间的等级相关系数来进行衡量。等级相关系数越高,则表明遗传评定(或育种值估计)的准确性越高。
采用马修斯校正系数(Matthews correlation index,MCI)法和三态片段交迭准确率(SOV)法对10 种某方法提取的蛋白质二级结构进行了预测,蛋白质二级结构真实值(TRUE)的数据采用计算机模拟产生,具体数据见表6.7。
表6.7 不同方法预测蛋白质二级结构评分表

续表

试比较两种预测方法预测蛋白质二级结构的准确性。
SAS 程序如图6.25 所示。

图6.25 两种预测方法预测蛋白质二级结构的准确性SAS 程序
输出结果为:
结果表明,马修斯校正系数(Matthews correlation index,MCI)法的蛋白质二级结构的准确性和三态片段交迭准确率(SOV)法的蛋白质二级结构的准确性与蛋白质二级结构真实值(TRUE)之间的等级相关关系数分别为0.709 09 和0.745 45,都达到了显著水平(P<0.05)。其中SOV 法的蛋白质二级结构的准确性与蛋白质二级结构真实值的等级相关系数高于MCI法,说明采用SOV 法进行蛋白质二级结构的预测的准确定要高于MCI 法。
SAS 程序如图6.26 所示。

图6.26 例6.4SAS 程序图(5)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




