回归分析：揭示变量间回归关系的分析

在动物科学研究中，人们对变量的相互关系进行分析时，除了要了解变量间相关的性质和密切程度（变量间是平衡或相互制约、部分主次的关系）外，更多的是要揭示出一个（或多个）变量随其他变量变化而变化的单向从属关系，即回归关系。习惯上将独立变化的变量称为自变量，而依赖自变量变化的变量称为因变量。确定变量间回归关系的分析即是回归分析，其主要内容就是通过建立回归方程来揭示变量间的这种回归关系，并据此从自变量的变化去估计因变量的变化。根据所涉及自变量数目的多少，又将两个变量间的回归（即只涉及一个自变量）称为直线回归（Linear Regression）或一元回归；而涉及多个自变量的回归称为多元回归（Multiple Regression）。

直线回归是用直线回归方程表示两个数量变量间依存关系的统计分析方法，属于双变量分析的范畴。如果某一个变量随着另一个变量的变化而变化，并且它们的变化在直角坐标系中呈直线趋势，就可以用一个直线方程来定量地描述它们之间的数量依存关系。直线回归分析的任务在于找出两个变量有依存关系的直线方程，以确定一条最接近于各实测点的直线，使各实测点与该线的纵向距离的平方和为最小。这个方程称为直线回归方程，据此方程描绘的直线就是回归直线。

多元线性回归分析也称为复线性回归分析，是一元线性回归分析或简单线性回归分析的推广，研究的是一组自变量X 如何直接影响一个因变量Y。这里的自变量X 指的是能够独立自由变化的变量，因变量Y 指的是非独立的、受其他变量影响的变量。由于多元线性回归分析（包括一元线性回归分析）仅涉及一个因变量Y，因此有时候也称为单变量线性回归分析。多元线性回归分析的手段，是借助于数学模型来计算总体中n 个自变量X 与一个因变量Y 之间的线性依存关系，并估计这个数学模型所拟合的相关变化规律的准确性。换句话说，多元线性回归分析可以从统计意义上确定在消除了其他自变量的影响后，每一个自变量的变化是否引起因变量的变化，并且估计出在其他自变量固定不变的情况下，每个自变量对因变量的数值影响的大小。多元线性回归模型包含多个解释变量，多个解释变量同时对被解释变量Y发生作用，若要考察其中一个解释变量对Y 的影响，就必须结合其他解释变量保持不变来进行分析。因此多元线性回归模型中的回归系数称为偏回归系数，即反映了当模型中的其他变量不变时，其中一个解释变量对因变量Y 的均值的影响。因此，多元线性回归分析主要解决：①各个自变量对因变量的各自效应，即偏回归系数（partial regression coefficient）；②建立由自变量描述和预测因变量的多元回归方程，并计算标准误；③对自变量进行选择，建立“最优”回归方程；④评定各个自变量对因变量的相对重要性，激进型通径分析（path analysis）。

（一）REG 过程

1.调用格式

PROC REG <选项列表>；

MODEL 应变量列表= <自变量/选项列表>；

BY 变量名列表；

FREQ 变量名；

ID 变量名列表；

VAR 变量名列表；

WEIGHT 变量名；

ADD 变量名列表；

DELETE 变量名列表；

MTEST <方程式<，…，方程式> > < /选项列表>；

OUTPUT <OUT=数据集名> keyword=变量名列表<…keyword=变量名列表>；

PRINT 选项；

PLOT <y 变量名×x 变量名> <=符号> <…y 变量名×x 变量名> <=符号> < /选项列表>；

上述语句中，PROC REG 语句和MODEL 语句是必须的，其他语句都是可选择的。

2.语句说明

（1）PROC REG 语句

用于调用REG 过程进行回归分析。其常用的选项主要有：

①数据集选项DATA=SAS 数据集，指定分析数据集，如果缺省，则对最新创建的数据集进行分析；OUTEST=SAS 数据集，要求将参数估计和选择的统计量输出到SAS 数据集中等。

②结果输出选项CORR，对在MODEL 和VAR 语句中列出的所有变量计算简单相关系数，并输出相关系数矩阵；SIMPLE，对用REG 过程进行分析的每个变量输出所有观测值的总和、均值、标准差和平方和等简单统计量。

（2）MODEL 语句

定义所用的回归分析数学模型。在MODEL 语句中出现的变量必须是用于分析数据集中的数值型变量。如想考虑模型中X1 的二次项，不能在MODEL 语句中使用X1 ×X1，而必须用DATA 步骤产生一个新变量（如X1SQUARE=X1 ×X1），然后再在MODEL 语句中使用这个新变量。MODEL 语句常用的选项主要有：

①SELECTION=模型选择方法。用于规定选择模型的方法，包括MONE（全回归模型）、STEPWISE（逐步回归）、FORWARD（逐个选入）、BACKWARD（逐个剔除）、MAXR（最大R2增量法）、MINR（最小R2增量法）、RSQUARE（所有可能的R2）、CP（总平方误差法）和ADJRSQ（调整的R2法），共9 种方法。其中在畜牧实验数据分析中，以前4 种方法最为常用。该选项缺省时，模型选择方法为NONE。

②INCLUDE=n。指定列在MODEL 语句中的前n 个自变量必须包含在模型中，筛选变量的方法仅对MODEL 语句中的其他变量进行。当使用SELECTION= NONE 选项时，该选项无效。

③NOINT。取消通常包含在模型中的常数项（即截距）。

④SLENTRY（或SLE）=概率值。对FORWARD 和STEPWISE 方法规定变量选入回归模型里的显著水平。对FORWARD 方法，其缺省值为0.50，而对STEPWISE 方法则为0.15。

⑤SLSTAY（或SLS）=概率值。对BACKWARD 和STEPWISE 方法规定变量保留在模型里的显著水平。对BACKWARD 方法而言，其缺省值为0.10，而对STEPWISE 方法则为0.15。

⑥结果输出选项。STB 为标准偏回归系数（即直接通经系数）；CLM 和CLI 分别为条件总体平均数的置信区间和观察值的预测区间；P 为预测值；R 为离回归误差分析；ALL 为所有输出项等。

（3）BY 语句

指定分类变量，以便得到由BY 变量定义的几个观测组的独立分析。当出现BY 语句时，过程要求输入数据实现已按BY 变量进行了排序。

（4）WEIGHT 语句

指定加权系数变量。

（5）PRINT 语句

打印分析结果。其选项除了MODEL 语句中的输出选项如STB 外，还有ANOVA（输出当前模型的方差分析表）；MODELDATA（配合模型使用的数据）等。

（6）PLOT 语句

用于画散点图。

3.结果输出

REG 过程输出的结果包括方差分析过程及相关的统计量，参数的估计值及其有关统计量以及其他选择性的结果输出内容。在进行多元回归分析时，如果设定了模型选择方法，则会输出模型选择的具体过程。

（二）GLM 过程

用于回归分析时，其调用格式与方差分析时基本相同的，只需设定相应的选项即可用于进行灵活的回归分析。尽管如此，为方便叙述，现仍对GLM 用于回归分析的使用作一简单介绍。

1.调用格式

　　　PROC GLM 选项；

　　　MODEL 因变量=自变量/选项；

应用GLM 过程进行回归分析时，上述两个语句都是必需的。

2.语句说明

由于其他语句的功能及使用与方法分析是一样的，这里只对MODEL 语句进行说明。

MODEL 语句的作用是用于定义回归分析的模型。使用选项SOLUTION 即可给出回归模型相应的参数估计值，从而建立用自变量估计因变量的线性回归方程。

在利用GLM 进行回归分析时，其方法不如REG 过程灵活，无法进行模型选择的STEPWISE、FORWARD、BACKWARD 等选择性操作，因而在实际进行回归分析时，一般都采用REG过程进行。

3.结果输出

采用GLM 过程进行回归分析时，其输出结果包括回归模型的显著性检验（方差分析）、自变量对因变量影响的显著性检验，以及回归模型的参数估计值及其显著性检验等内容。

（三）直线回归分析的示例应用

例6.1　四川白鹅的雏鹅重（g）与70 日龄重（g）的12 对实际观测值见表6.1，建立四川白鹅70 日龄重y 与雏鹅重x 的直线回归方程。

表6.1　四川白鹅的雏鹅重与70 日龄重12 对实际观测值

试分析雏鹅重与70 日龄重的测定结果是否存在直线回归关系。

SAS 程序如图6.1 所示。

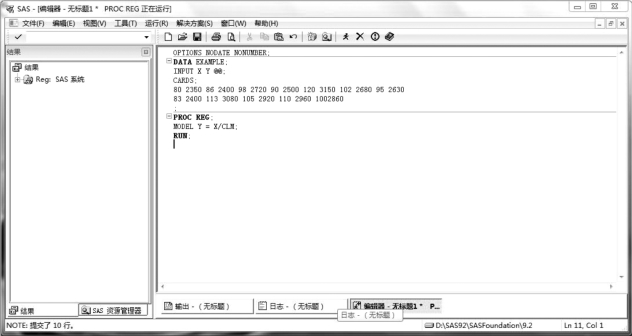
图6.1　雏鹅重与70 日龄重直线回归SAS 程序

输出结果为：

1.方差分析过程

方差分析结果表明模型拟合数据较好（F=285.82，P<0.000 1），说明回归方程是有意义的。其中Root MSE 为误差均方的平方根（即剩余标准差），本例题中Root MSE 为52.427 54，剩余标准差与均数之比即为变异系数（C.V.）。决定系数（R-square）和矫正决定系数（Adj Rsq）的值为0 ～1，它表示回归方程中由自变量可线性说明因变量变异的比例，反映的是所建立的回归方程的可靠性，决定系数越大，说明所建立的回归方程的可靠性越高。本例题中，相关系数R2=0.969 5，意味着因变量Y 的总体变异中96.95%被自变量X 所解释，表明所建立的回归方程具有很高的可靠性。

SAS 程序如图6.2 所示。

图6.2　例6.1SAS 程序图（1）

2.回归模型的参数估计

本部分结果表明所建立的回归方程的各项参数的估计值，其中包括回归方程中的截距（常数项，Intercept）和自变量X 的回归系数及其标准误，以及各项估计值的显著性检验。本例题中，常数项（截距）a=582.691 81，P=0.001 3 <0.01，差异极显著，自变量X 的回归系数b=21.608 49，P<0.000 1，差异极显著。表明各项的参数估计具有显著性意义。由此建立的由X 估计Y 的线性回归方程为：

Y=582.691 81 +21.608 49X

结合方差分析过程中的决定系数值（R2=0.969 5），可以认为所建立的回归方程具有较高的可靠性。

SAS 程序如图6.3 所示。

图6.3　例6.1SAS 程序图（2）(www.xing528.com)

3.回归方程预测的预测值、置信区间和准确性

本部分结果输出因变量Y 的描述统计量，包括序号、观察值、预测值、预测值的标准误、预测值的95%置信区间、残差。本例题中用Y 的观察值2 350 所预测的Y 的值为2 311，其标准误为28.297 9，在该估计值95%的置信区间下限和上限分别为2 247 和2 375，相应的剩余值（残差）为38.628 7。

SAS 程序如图6.4 所示。

图6.4　例6.1SAS 程序图（3）

（四）多元直线回归分析的示例应用

例6.2　成年牛的体重是牛育种的重要指标。测定了20 只大通牦牛成年牛的体长（LENHTH，cm）、胸围（CHEST，cm）和体重（WEIGHT，kg），数据见表6.2。

表6.2　20 只大通牦牛成年牛的体长、胸围和体重数据表

试用REG 过程绘制该品种牛由体长和胸围估计其成年体重的二元回归方程。

SAS 程序如图6.5 所示。

图6.5　体长和胸围估计其成年体重二元回归分析SAS 程序

输出结果为：

1.方差分析

二元线性回归模型的方差分析结果，F=36.22，P <0.000 1，差异极显著，表明该回归方程具有显著的统计学意义。

SAS 程序如图6.6 所示。

图6.6　例6.2SAS 程序图（1）

2.回归模型的参数估计

模型参数估计结果，a= -669.937 87（P <0.000 1），b=2.922 12（P=0.001 5 <0.01），c=3.700 92（P<0.000 1），都达到了极显著水平，表明大通牦牛的成年体重（Y，WEIGHT）与体长（X1，LENGTH）和胸围（X2，CHEST）之间存在显著的线性关系，相应的回归方程为：

Y= -669.937 87 +2.922 12X1+3.700 92X2

决定系数R2=0.809 9，表明所建立的由体长和胸围估计大通牦牛成年体重的回归方程具有较高的可靠性。

SAS 程序如图6.7 所示。

图6.7　例6.2SAS 程序图（2）

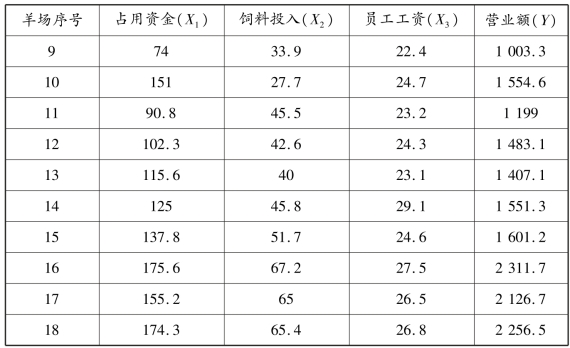
例6.3　青海省某地区统计局统计其地区18 个养殖场的羊只占用资金情况、饲料投入费用、员工工资以及营业额等方面数据，见表6.3。该地区统计局试图根据这些数据找到营业额与其他3 个变量之间的关系，以便进行营业额预测并为未来藏羊养殖体系转型工作提供参考。根据这些数据建立回归模型并计算y 与X1，X2和X3的相关系数。

表6.3　18 个养殖场羊只占用资金、饲料投入、员工工资及营业额统计表

续表

SAS 程序如图6.8 所示。

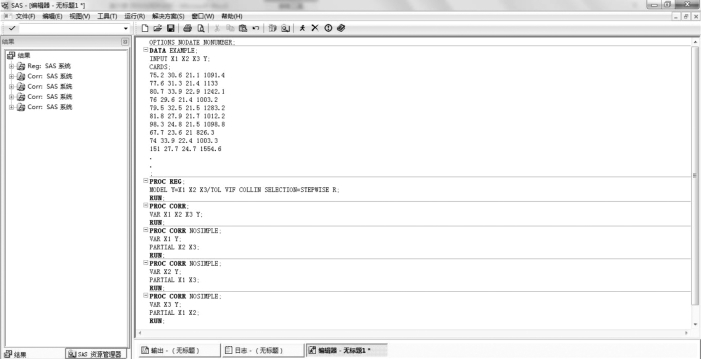
图6.8　养殖场羊只占用资金、饲料投入、员工工资及营业额回归分析SAS 程序

注：为展现完整的程序步骤，数据为部分数据。

输出结果为：

1.方差分析

三元线性回归模型的方差分析结果，变量X1进入模型之中，模型检验结果为：F=130.22，P<0.000 1；模型有显著性意义。参数X1检验结果为F=130.22，P <0.0001，参数X1有显著性意义。

SAS 程序如图6.9 所示。

图6.9　例6.3SAS 程序图（1）

变量X2进入模型之中，模型检验结果为：F=168.11，P <0.000 1，模型有显著性意义。参数X1检验结果为：F=42.10，P <0.000 1，参数X2检验结果为：F=23.45，P=0.000 2 <0.01。参数X1和X2都有显著性意义。

SAS 程序如图6.10 所示。

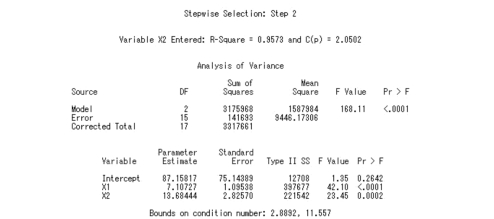
图6.10　例6.3SAS 程序图（2）

对上述变量的逐渐选择过程进行总结描述，这是所有留在模型中的变量满足停留允许水平0.05，并且模型外的所有变量不满足进入允许水平，因此筛选过程结束。

SAS 程序如图6.11 所示。

图6.11　例6.3SAS 程序图（3）

模型的总体方差分析结果，逐步过程法得到的最后模型拟合很好（F=168.11，P<0.000 1，R2=0.957 3）。

SAS 程序如图6.12 所示。

2.回归模型的参数估计

参数检验结果表明，变量X1（P<0.000 1）和X2（P=0.000 2）的偏回归系数与零差异均显著。共线性检验结果表明，观察第2 列条件指数，条件数为12.226 92，大于10，因此数据可能存在内相关性。从最后两行可以看出，变量X1和X2的方差比例值很大，因此这两个变量可能有共线性，但是由于条件数不是很大，共线性影响不大。

图6.12　例6.3SAS 程序图（4）

SAS 程序如图6.13 所示。

图6.13　例6.3SAS 程序图（5）

因变量Y 的描述统计量，包括序号、观察值、预测值、预测值的标准误、残差、残差的标准误和学生残差等，接下来是学生残差的直方图，最后一列是Cook 的距离残差D。因为所有的学生残差的绝对值小于2（满足要求），所有的Cook’s D 小于0.5，所以可以认为数据中没有极端点。据此可以得出结论：营业额与养殖占用资金和饲料投入的费用有关，其线性模型如下：

Y=87.158 17 +7.107 27X1+13.684 44X2

SAS 程序如图6.14 所示。

图6.14　例6.3SAS 程序图（6）

3.偏相关系数的估计

通过偏相关系数的检验结果可知：①给出4 个变量的描述统计量，包括均数、标准差、累加值、最大值和最小值。②每一对变量的简单相关系数估计值以及统计检验结果，如X1和X2的简单相关系数为0.808 63，P<0.000 1。③每一对变量的偏相关系数，如X1与Y 的偏相关系数为0.820 80，P<0.000 1，差异极显著；X2与Y 的偏相关系数为0.762 26，P<0.000 1，差异极显著；X3与Y 的偏相关系数为-0.059 74，P=0.826 0 >0.05，差异不显著。结果表明，X1和X2与Y 有显著的相关性，X3与Y 相关性差异不显著。与上述计算结果一致。

SAS 程序如图6.15—图6.18 所示。

图6.15　例6.3SAS 程序图（7）

图6.16　例6.3SAS 程序图（8）

图6.17　例6.3SAS 程序图（9）

图6.18　例6.3SAS 程序图（10）