独立性检验的SAS检验方法

（一）2 ×2 列联表的独立性检验

例5.3　为了检验某种疫苗的免疫效果，某猪场用80 头猪试验。接种疫苗的44 头猪有12 头发病，32 头未发病；未接种疫苗的36 头猪有22 头发病，14 头未发病。检验该疫苗是否有免疫效果？

在本题中，将因素的各个水平（接种疫苗和未接种疫苗）作为横标目，将质量性状的各个属性类别（发病和未发病）作为纵标目，行数为因素的水平数2，列数为质量性状的各个属性类别数2。因此，本例题为2 ×2 列联表的独立性检验（表5.2）。

SAS 程序如图5.6 所示。

表5.2　接种疫苗与未接种疫苗和发病与未发病的2 ×2 列联表

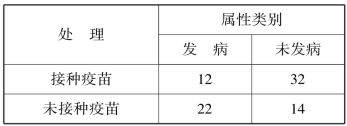
图5.6　例5.3 SAS 程序图（1）

输出结果为：

这是一个2 ×2 列联表独立性检验问题，df=（2 -1）（2 -1）=1，进行χ2检验须作连续性矫正。本例χ2检验的结果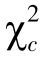，=7.944 4，P=0.004 8 <0.05，表明猪发病率与接种疫苗有关，接种与未接种疫苗猪发病率差异显著，这里表现为接种疫苗猪的发病率显著低于未接种疫苗猪的发病率，说明该疫苗免疫效果显著。

SAS 程序如图5.7、图5.8 所示。

图5.7　例5.3 SAS 程序图（2）

图5.8　例5.3 SAS 程序图（3）

（二）2 ×c 列联表的独立性检验

例5.4　在甲、乙两地进行水牛体型调查，将体型按优、良、中、差4 个等级分类，结果见表5.3。检验甲、乙两地水牛体型的构成比是否相同？

SAS 程序如图5.9 所示。

表5.3　两地水牛体型4 个等级的2 ×4 列联表

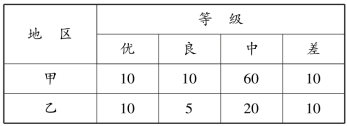
图5.9　例5.4 SAS 程序图（1）

输出结果为：在本2 ×4 列联表中，因素的各个水平（甲地和乙地）为横标目、水牛体型的等级（优、良、中、差）为总标目，df=（2 -1）（4 -1）=3，无须作连续性矫正。本例χ2检验的结果，χ2=7.500 0，P=0.056 7 >0.05，表明甲、乙两地水牛体型4 个等级构成比差异不显著，即甲、乙两地水牛体型4 个等级构成比相同。

SAS 程序如图5.10、图5.11 所示。

图5.10　例5.4 SAS 程序图（2）

图5.11　例5.4 SAS 程序图（3）

此外，进行动物科学试验研究，有时候需要将数量性状资料转化为等级资料。例如剪毛量分为特等、一等、二等，产奶量分为高产、中产、低产。对这样的等级资料也可采用χ2检验进行假设检验。同时，对双向无序的2 ×c（r ×c）列联表资料，当用χ2检验作出拒绝H0的结论时，研究者常需要指导更进一步的情况，此时就需要对资料进行分割，2 ×c（r ×c）列联表变成一系列的2 ×2 列联表形式，然后逐一分析这些分割后的资料，以便给出尽可能细致的回答。

χ2分布的多个变量之和也服从χ2分布，因此一个较大的χ2值，根据分析的目的，可以分割成n 个分量，多个样本率比较的资料可整理成2 ×2 列联表，经2 ×c（r ×c）列联表资料χ2检验的结果为拒绝H0，接受HA时，若不经任何处理，而直接用分割法把2 ×c（r ×c）列联表χ2分布分成多个独立的2 ×2 列联表进行两两比较，则需要重新规定检验水平。重新规定检验水平的估计方法通常有以下两种情况：①多个试验组与一个对照组的比较，需要对每次检验的显著水平重新规定，即α′=α/[2（k -1）]，k 为总组数（包括对照组）。②多个试验组之间的两两比较，α′=α/[k（k-1）/2 +1]。

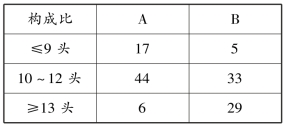
例5.5　统计A、B 两个品种各67 头经产母猪的产仔数，按照产仔数≤9 头、10 ～12 头，≥13 头3 个等级统计经产母猪头数，见表5.4，检验A、B 两品种经产母猪产仔数的3 个等级构成比是否相同。

SAS 程序如图5.12 所示。

表5.4　A、B 两个品种经产母猪产仔数3 个等级的2 ×3 列联表

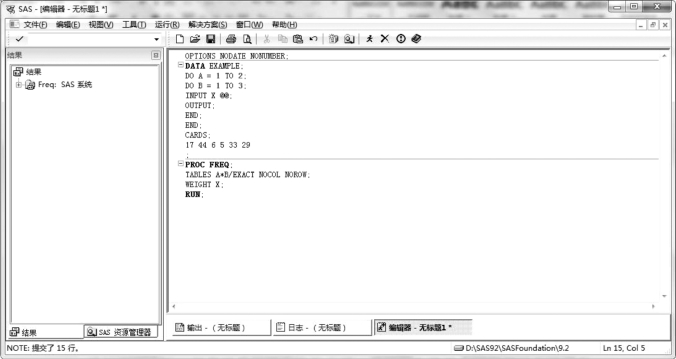
图5.12　例5.5 SAS 程序图（1）

输出结果为：在本2 ×3 联表中，因素的各个水平（品种A 和品种B）为横标目、数量性状资料（产仔数）转化为等级资料的各个等级为纵标目，df=（2 -1）（3 -1）=2，无须做连续性矫正。本例χ2检验的结果，χ2=23.231 2，P<0.01，表明经产母猪产仔数3 个等级的构成比与品种差异极显著，有必要进一步检验，以确定3 个等级的构成比差异极显著在哪样的等级。

SAS 程序如图5.13 所示。

图5.13　例5.5 SAS 程序图（2）

本例题中，通过检验确定3 个等级的构成比差异，因此，根据资料进行两两比较，以分析是否任意两个等级在两个品种中有显著性差异，则表5.4 需转化为表5.5。

表5.5　3 个等级构成比差异的比较

检验步骤如下：

①提出无效假设与备择假设：

H0：μA=μB，即任意两对比组的构成比相同；

HA：μA≠μB，即任意两对比组的构成比不同。

②本例为3 个等级之间的两两比较，设α=0.05，其检验水平如下：

③分别计算任意两对比组的检验统计量χ2值与P 值，所得P 值结果与α′比较，进而得出结论结果见表5.6。

表5.6　3 个等级之间两两比较结果

由表5.6 得，按α′=0.012 5 的检验水准，P（≤9 头vs.10 ～12 头）=0.143 3 >0.012 5，表明两个等级之间差异不显著，即A、B 两组经产母猪产仔数在≤9 头与10 ～12 头两个等级的构成比相同；P（≤9 头vs.≥13 头）<0.012 5，表明两个等级之间差异显著，即A、B 两组经产母猪产仔数在≤9 头与≥13 头两个等级的构成比不同；P（10 ～12 头vs.≥13 头）=0.000 2 <

0.012 5，表明两个等级之间差异显著，即A、B 两组经产母猪产仔数在10 ～12 头与≥13 头两个等级的构成比不同。

（三）r×c 列联表的独立性检验

r×c 列联表可以分为双向无序、单向有序、双向有序属性相同和双向有序属性不同等4 类。

（1）双向无序r×c 列联表

表中两个分类变量皆为无序分类变量，对于该类资料，①若研究目的为多个样本率（或构成比）的比较，可用r×c 列联表的χ2检验；②若研究目的为分析两个分类变量之间有无关联性以及关系的密切程度，可以用r×c 列联表的χ2检验，以及Pearson 列联系数进行分析。

（2）单向有序r×c 列联表

单向有序r×c 列联表有两种形式，一种是r×c 列联表中的分组变量（横标目）是有序的，而指标变量（纵标目）是无序的，此种单向有序r ×c 列联表可以用r ×c 列联表的χ2检验进行分析；另一种情况是r×c 列联表中的分组变量（横标目）是无序的，而指标变量（纵标目）是有序的，此种单向有序r×c 列联表资料宜用秩和检验进行分析。

（3）双向有序属性相同的r×c 列联表

表中的两个分类变量皆为有序且属性相同，实际上是2 ×2 配对设计的扩展，此时宜用一致性检验（或称Kappa 检验）。

（4）双向有序属性不同的r×c 列联表

表中的两个分类变量皆为有序且属性不相同，对该类资料需要分析两个有序分类变量间是否存在线性变化趋势，宜用有序分组资料的线性趋势检验。

例5.6　将117 头奶牛随机分为3 组，每组39 头，分别饲喂3 种不同的饲料，观察记载各组39 头奶牛每头奶牛的发病次数，以奶牛发病次数0、1、2、…、9 作为奶牛发病的10 个等级，奶牛发病10 个等级与饲喂3 种饲料的10 ×3 列联表见表5.7。检验奶牛发病等级的构成比与所饲喂的饲料种类是否有关。

表5.7　奶牛发病10 个等级与饲喂3 种饲料的10 ×3 列联表

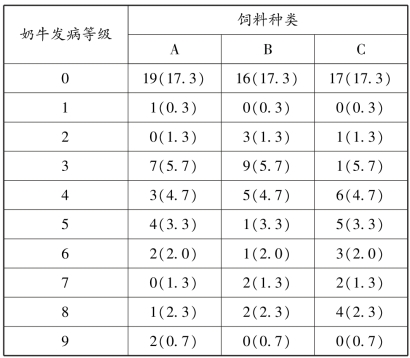
这是一个行变量为顺序变量的χ2检验，在列联表5.7 中，奶牛发病的等级为横标目，因素（饲料种类）的水平为纵标目，行数为奶牛发病的等级数10，列数为因素（饲料种类）的水平数3，在做这个列联表中，括号内的数据为各个等级的实际观察次数对应的理论次数，对于理论次数小于5 者，须将其与相邻等级合并，合并等级后各个等级的理论次数大于5。表5.7 为合并后列联表，行数为合并等级后的等级数4，列数仍为因素（饲料种类）的水平数3，这是一个4 ×3列联表行变量为顺序变量的χ2检验。

变量虽然是有序的，但毕竟不是定量的，需要给有序变量的各个等级赋值，方可进行相关性分析。最简单的赋值方法是按顺序赋给秩次（即得分），即给行变量的等级赋值1、2、…、R和给列变量的等级赋值1、2、…、C。这样（X，Y）的取值就有R ×C 对，表中的R ×C 个频数就是这个R×C 对取值所对应的频数，然后计算Spearman 秩相关系数，并作显著性检验，这就是比较粗糙的分析方法。

合并等级后的4 ×3 列联表见表5.8。

SAS 程序如图5.14 所示。(https://www.xing528.com)

表5.8　合并等级后的4 ×3 列联表

图5.14　例5.6 SAS 程序图（1）

输出结果为：①给出了两个变量的描述性统计量；②给出变量的秩相关系数矩阵（VAR语句所列变量中人两者之间的相关系数），相关系数部位零（r= -0.093 39，P=0.125 8）。可以得出结论，奶牛发病4 个等级的构成比与饲料种类无关，可以认为用此3 种饲料饲喂奶牛，奶牛发病4 个等级的构成比相同。

SAS 程序如图5.15 所示。

图5.15　例5.6 SAS 程序图（2）

例5.7　猪瘟的治疗效果分为治愈、显效、好转和无效，为了评价某兽医研究所研究的3种治疗猪瘟的药物A、B、C 对该种疾病的治疗效果，将3 种药物的治疗资料整理成表5.9，试分析3 种药物的治疗效果是否存在差异？

表5.9　药物疗效对比

这种资料用一般的χ2检验只能得出两组构成比是否相同的结论，并不能得出哪组疗效较好的结论。例如，当实验组无效和治愈较多，对照组则好转和显效较多，此时χ2怎会较大，P值则较小，说明其构成比不同，但不能说明何者疗效好。

本题是列变量为顺序变量的χ2检验，其计算方法为，认为给各疗效一个分数，如无效为1，好转为2，显效为3，治愈为4，则可计算其均数，称为行平均得分。由此，可以计算出各行的行平均得分，然后比较各行的行平均得分是否差异显著，从而说明哪种药物的疗效好。

进行行均分检验的SAS 程序为FREQ 过程，此时需要在Tables 语句后面增加CMH 选项，即求统计量Cochran-Mantel-Haenszel。

SAS 程序如图5.16 所示。

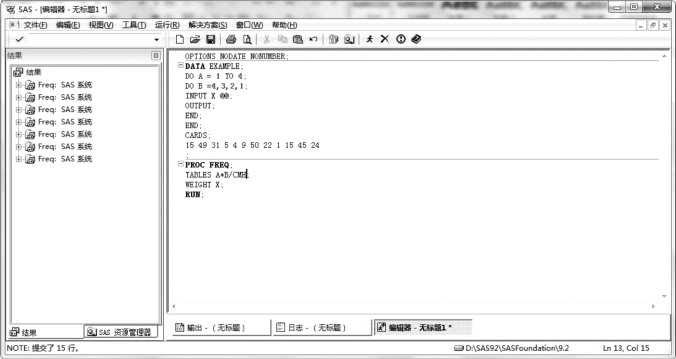
图5.16　例5.7 SAS 程序图（1）

输出结果为：①本结果中列出了列联表频数及各百分比，与前面相同；②本结果中输出了χ2值及相关系数；③本结果中，行均值得分差值即Qs值。Qs=58.677 8，P <0.000 1，据此可得出结论：3 种药物的治疗效果有显著性差异。

这样的数据也可以采用Logitic 回归分析模型，将列变量作为因变量，将行变量作为自变量进行数据分析。此部分下面章节将进行详细介绍。

SAS 程序如图5.17 所示。

图5.17　例5.7SAS 程序图（2）

例5.8　某兽医研究所用某种兽药进行抑菌试验，将用药后对革兰氏阳性菌与革兰氏阴性菌的抑菌效果整理成列联表（表5.10），现进行药物对革兰氏阳性菌与革兰氏阴性菌抑菌效果一致性检验。

表5.10　革兰氏阳性菌与革兰氏阴性菌抑菌效果比较分析

本题为双向有序属性相同r×c 列联表资料的统计分析，其SAS 程序如图5.18 所示。

图5.18　例5.8SAS 程序图（1）

SAS 输出结果如下：①输出变量的频数分布以及百分数；②输出“对称性”检验结果，以及配对检验的显著性推断；③输出Kappa 检验结果，Kappa=0.186 5，表明药物的抑菌效果对革兰氏阳性菌与革兰氏阴性菌的一致性较差。据此可以得出结论，该药物对革兰氏阳性菌和革兰氏阴性菌抑菌效果有显著性差异，一致性较差。

SAS 程序如图5.19、图5.20 所示。

图5.19　例5.8SAS 程序图（2）

图5.20　例5.8SAS 程序图（3）

例5.9　为研究家禽新城疫与近期使用抗生素之间的关系，在5 个养鸡场中采用病鸡—对照研究方法调查了234 只新城疫鸡与1 742 只对照者（正常鸡）使用口服抗生素状况，资料见表5.11，请在排除了5 个养鸡场的影响后，分析使用口服抗生素对是否患新城疫的影响情况。SAS 程序如图5.21 所示。

表5.11　新城疫与近期使用口服抗生素关系的调查结果

续表

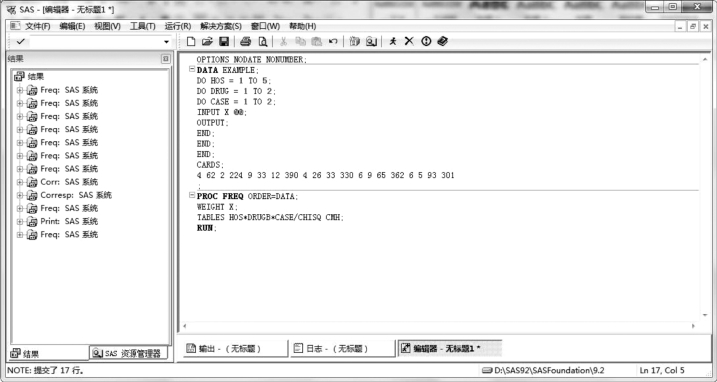
图5.21　例5.9SAS 程序图（1）

SAS 输出结果如下：①分别输出第1 ～5 家养殖场的四格表频数、百分数、χ2检验、Fisher精确检验结果及相关内容；②输出CMH 选项的统计分析结果。首先输出Cochran-Mantel-Haenszel 统计量，其中检验了非零相关、行平均得分差及一般关联等3 个备选假设，这三者在四格表资料中的结果是相同的，因而不必考虑应当选择哪一个结果。这里是检验口服抗生素与新城疫的关系，但矫正了养殖场的差异作用，有分析结果可见，QMH=34.723 0，P<0.000 1，据此可以得出结论，是否使用抗生素与新城疫显著相关；③输出对优比的齐性Breslow-Day 检验是检验服药组与不服药组与是否发生新城疫的关联在各中心是否一致，本例QMH=6.405 1，DF=4，P= 0.170 9，即不能认为各养殖场的优比（案例对照，OR）不同。如果Breslow-Day 的QMH有统计意义，则不能用总的OR 与总的疗效比较。

SAS 程序如图5.22—图5.25 所示。

例5.10　为了研究藏系绵羊毛色深浅程度是否与年龄相关，将资料整理成表5.12 的形式，试编写趋势卡方检验的SAS 程序，分析年龄与毛色深浅程度的相关关系。

图5.22　例5.10SAS 程序图（1）

图5.23　例5.10SAS 程序图（2）

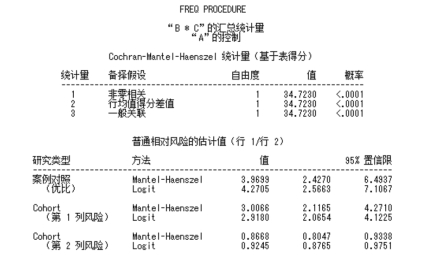
图5.24　例5.10SAS 程序图（3）

图5.25　例5.10SAS 程序图（4）

表5.12　毛色深浅程度与年龄的关系

如果两个有序变量之间有相关关系，则需要进一步研究两个变量之间是否呈直线变化关系，这就需要进行趋势χ2检验。进行趋势χ2检验，首先应计算r×c 列联表的χ2值，然后将总的χ2值分解成线性回归分量与偏离线性回归分量，若两分量有统计学意义，说明两分类变量存在相关关系，但关系不是简单的直线关系；若线性回归分量有统计学意义，偏离线性回归分量无统计学意义，说明两分类变量不仅存在相关关系，而且是线性关系，SAS 程序如图5.26、图5.27 所示。

图5.26　例5.10SAS 程序图（5）

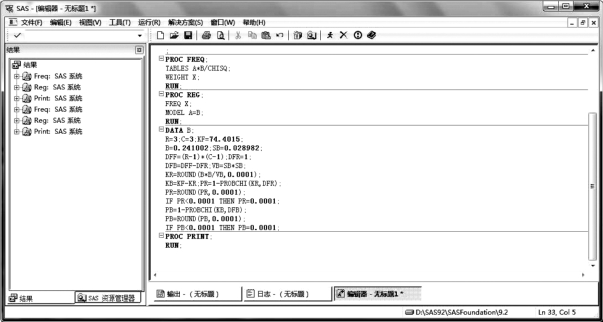
图5.27　例5.10SAS 程序图（6）

SAS 输出结果为：①输出变量的频数分布及百分数；②输出χ2统计量以及检验结果，Chi-Square=74.401 5（总的χ2值），df=4，P<0.000 1；③输出方差分析表，结果表明模型拟合数据较好（F=69.15，P<0.000 1），模型有显著性意义；④参数估计结果，自变量b 有显著性意义（P<0.000 1），常数项也有显著性意义（P=0.000 1）；⑤输出线性趋势检验的检验结果，根据χ2和回归分析结果，将总的χ2值分解为线性回归分量χ2回归和偏线性回归分量，并进行显著性检验。Pr=0.000 1，表明线性回归分量有显著性统计学意义。Pb=0.154 2，表明偏线性回归分量无显著性统计学意义。据此可以得出结论，毛色深浅程度与年龄呈直线相关。

SAS 程序如图5.28—图5.32 所示。

图5.28　例5.10SAS 程序图（7）

图5.29　例5.10SAS 程序图（8）

图5.30　例5.10SAS 程序图（9）

图5.31　例5.10SAS 程序图（10）

图5.32　例5.10SAS 程序图（11）