【摘要】:1899 年,统计学家K.Pearson 提出了用卡方作为检验实际观察次数与理论次数符合程度的检验统计量。(二)计算χ2值在这一步中,需要根据实际观察次数与理论次数计算出相应的χ2值。(三)统计推断将计算的实际χ2值与相应的显著水平的理论χ2值进行比较,如果实际χ2值小于理论χ2值,则表示差异不显著,接受H0;如果实际χ2值大于理论χ2值,则表示差异显著,否定H0,接受HA。
1899 年,统计学家K.Pearson 提出了用卡方(chi-square,χ2)作为检验实际观察次数与理论次数符合程度的检验统计量。进行次数资料的χ2检验,一般需经过如下3 个基本步骤:
(一)建立假说
对次数资料进行χ2检验,首先应建立相应的假设,无效假设H0为实际观察次数与理论次数的偏差为0,即两者是符合的(适合性检验);或两类因子之间是相互独立的(独立性检验)。相应的备择假设HA为实际观察次数与理论次数的偏差不等于0(适合性检验),或两类因子之间是有关联的(独立性检验)。
(二)计算χ2值
在这一步中,需要根据实际观察次数与理论次数计算出相应的χ2值。其中,在动物科学试验数据处理中常用的主要有以下几种:
(1)一般化的χ2值(https://www.xing528.com)
(2)连续性矫正χ2值
(3)似然比χ2值
在对大样本条件下的近似χ2分布资料进行检验时,需要计算似然比χ2值(likelihood ratio chi-square,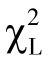 )。
)。
(三)统计推断
将计算的实际χ2值与相应的显著水平(α=0.05 或0.01)的理论χ2值进行比较,如果实际χ2值小于理论χ2值,则表示差异不显著(即实际观察次数与理论次数相符),接受H0;如果实际χ2值大于理论χ2值,则表示差异显著(即实际观察次数与理论次数不符),否定H0,接受HA。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




