SAS统计分析：统计数χ2的意义

次数资料的适合性或独立性检验的基本原理是根据观察次数与理论次数之间偏离程度的大小而定的。若观察次数与理论次数的偏差越大，则表示两者越不符合；偏差越小，两者就越符合；当两者相等（即偏差为0）时，表明理论次数与观察次数完全符合。

为了方便理解，结合实际例子来说明统计数χ2的意义。某养鱼场进行鲤鱼遗传试验，以荷包红鲤（红色、隐性）与湘江野鲤（青灰色、显性）为例，其F2 代获得1 602 尾鲤鱼，其中青灰色鲤鱼1 503 只，红色鲤鱼99 只。根据孟德尔遗传定律，按照3∶1的显隐比例，青灰色鲤鱼与红色鲤鱼的数量应为1 202 尾和400 尾。以A 表示实际观察次数，T 表示理论次数，可将此次数资料整理成列表5.1。

表5.1　鲤鱼体色实际观察次数与理论次数

(www.xing528.com)

从表5.1 可得，实际观察次数与理论次数有差异，青灰色和红色鲤鱼各相差301。这个差异属于随机误差（抽样误差）还是因为体色分离比例发生了实质性的变化？ 要回答这个问题，首先需要确定一个统计数以表示实际观察次数与理论次数的偏离程度；然后判断这一偏离程度是否属于随机误差，即进行假设检验。为了表示实际观察次数与理论次数的偏离程度，最简单的办法是求出实际观察次数与理论次数的差数。从表5.1 得知：A1-T1=301，A2-T2=-301，由于这两个差数之和为0，显然不能用这两个差数之和来表示实际观察次数与理论次数的偏离程度。为了避免两个差数正、负抵消，可将两个差数平方后再相加，即计算∑（AT）2，其值越大，实际观察次数与理论次数偏离程度就越大；反之，其值越小，实际观察次数与理论次数偏离程度就越小。但利用∑（A -T）2表示实际观察次数与理论次数的偏离程度尚有不足。例如，某一类别实际观察次数为505，理论次数为500，相差5；另一类别实际观察次数为26，理论次数为21，相差也为5，显然这两种类别实际观察次数与理论次数的偏离程度是不同的。为了弥补这一不足，可将各个差数平方除以相应的理论次数后再相加，并记为χ2，即χ2= ∑（A-T）2/T。也就是说χ2是表示实际观察次数与理论次数偏离程度的一个统计数，χ2小，表示实际观察次数与理论次数偏离程度小，χ2大，表示实际观察次数与理论次数偏离程度大；χ2=0，表示实际观察次数与理论次数完全吻合。次数资料是不连续性变异资料，为了表明实际观察次数与理论次数偏离程度引入的统计数χ2近似服从一种连续型随机变量的概率分布——χ2分布，由计算公式得，自由度不同，χ2分布的密度曲线也不同，图5.1 所示为自由度不同时，χ2分布的密度曲线。

图5.1　自由度不同时的卡方分布的密度曲线

根据图5.1 可知，对于次数资料进行χ2检验，利用连续型随机变量χ2分布计算的概率常常偏低，特别是当自由度为1 时，偏差较大。Yates 与1934 年提出了一个矫正公式，矫正后的χ2记为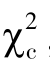，计算公式为。当自由度大于1 时，χ2分布接近连续型随机变量χ2分布，这时可不做连续性矫正，但要求各类别的理论次数不小于5。若某一类别理论次数小于5，则应把它与其相邻的一类别或几类别合并，直到合并类别后的理论次数大于5 为止。