SAS 统计分析中多重比较结果的应用实例

（一）单因素试验资料的方差分析

各个处理重复数相等的单因素试验资料的方差分析如下所述。

例4.1　随机抽测5 个品种各5 头母猪的窝产仔数并列于表4.1，检验5 个品种母猪窝产仔数是否有差异？

表4.1　5 个不同品种母猪的窝产仔数

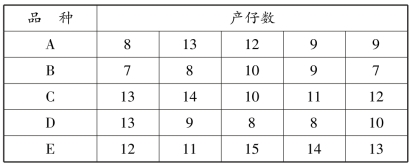
这是一个各个处理重复数相等的单因素试验资料，处理数k=5，各个处理重复数n=5，共有N=k×n=25 个观测值，其SAS 程序如图4.1 所示。

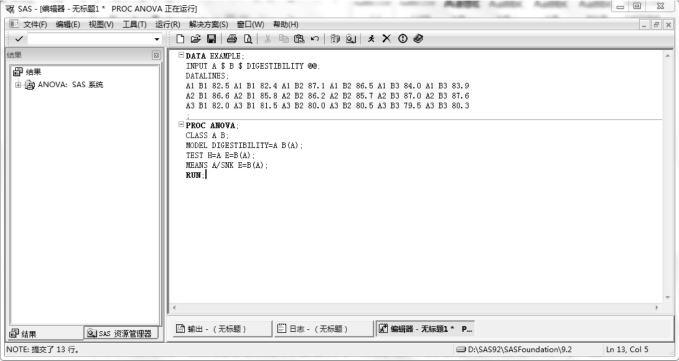
图4.1　各个处理重复数相等的单因素试验资料的方差分析SAS 程序

图4.1 为各个处理重复数相等的单因素试验资料的方差分析SAS 程序，PROC ANOVA过程为调用ANOVA 过程（即方差分析）；CLASS BREED 指明为BREED（品种）为分类变量（即以品种为分组的依据）；MODEL REPRODUCTION=BREED 指明模型为单因素主效应模型；MEANS BREED/SNK 用Q 值法作为多重比较的方法，默认的显著水平（α=0.05），此过程中若用DUNCAN 法作为多重比较，则需要标注MEANS BREED/DUNCAN，同理，用LSD 法作为多重比较，则需要标注MEANS BREED/LSD，若以α=0.01 作为显著检验水平，则需要在多重比较方法后标注MEANS BREED/SNK ALPHA=0.01。

输出结果为：

1.方差分析结果

该部分会输出变异来源（Source）、自由度（DF）、平方和（Sum of Squares）、均方（Square）、计算的实际F 值（F Value）大于临界F 值的概率（Pr>F）。对SAS 系统的各个处理重复数相等的单因素试验资料的方差分析结果输出，人们只需要根据概率值就可以对方差分析的结果作出判断。本例中，F=5.83，P（Pr >F 值）=0.002 8 <0.05，表明不同品种母猪窝产仔数存在显著性差异。因此需要对此数据进行多重比较，具体如图4.2 所示。

图4.2　各个处理重复数相等的单因素试验资料的方差分析

2.多重比较

该部分对不同处理均数间的差异显著性在规定的显著性水平上进行多重比较。SAS 统计分析中多重比较结果采用的是标记字母法。各组平均数间凡有一个相同字母标记的即为差异不显著，凡无相同字母标记的即为差异显著。本例中，分别采用了LSD 法（图4.3）、SNK法（图4.4）、DUNCAN 法（图4.5）及SNK 法（α=0.01）（图4.6）多重比较结果。以默认LSD法进行讲解（图4.3），由结果可知， E 组母猪窝产仔数显著高于A、D、B 组（P<0.05），E 组母猪窝产仔数与C 组母猪窝产仔数差异不显著（P>0.05）；C 组母猪窝产仔数显著高于D、B 组（P<0.05），C 组母猪窝产仔数与A 组母猪窝产仔数差异不显著（P >0.05）；A、D、B 组母猪窝产仔数差异不显著（P>0.05）。

图4.3　各个处理重复数相等的单因素试验资料的LSD 法多重比较

图4.4　各个处理重复数相等的单因素试验资料SNK 法多重比较

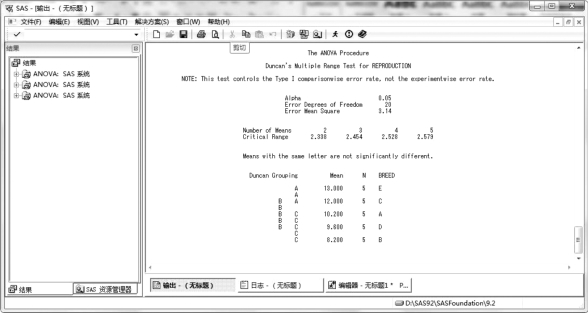
图4.5　各个处理重复数相等的单因素试验资料DUNCAN 法多重比较

图4.6　各个处理重复数相等的单因素试验资料SNK 法（α=0.01）多重比较

在实际工作过程中，常常需要分析同一因素对不同指标的影响（即在同一个因素影响下，对不同指标分别进行单因素分析）。如在上述例子中，如果还记录了其他指标，则只需要将上述程序中的MODEL 语句和MEANS 语句做适当修改就可以通过一次单因素方差分析进行多个指标的分析。当然，DATALINES 中的数据内容也要相对地发生变化，INPUT 语句中的变量也要随之进行相应的改变。

例4.2　为了比较青海互助八眉猪与不同引进品种猪的二元杂交效果，分别采用长白猪、大白猪、杜洛克和汉普夏做父本与青海互助八眉猪母本进行杂交，对杂交后代各组分别抽取6头母猪（假定母猪的饲养管理条件和胎次都相同），进行产仔数（LS）和断奶仔猪数（LSW）的比较分析，具体数据见表4.2。其SAS 分析程序如图4.7 所示。

表4.2　不同二元杂交效果母猪产仔猪和断奶仔猪数

图4.7 所示为同一因素对不同指标方差分析SAS 程序，PROC ANOVA 过程为调用ANOVA过程（即方差分析）；CLASS BREED 指明BREED（品种）为分类变量（即以品种为分组的依据）；MODEL LS LSW=BREED 指明模型为单因素主效应模型的数学模型；MEANS BREED/DUNCAN用DUNCAN 法作为多重比较的方法，默认显著水平（α=0.05）。

输出结果为：

1.方差分析结果

方差分析结果（图4.8），对产仔数（LS）而言，F=9.04，P=0.000 6 <0.05，说明不同杂交组合母猪在产仔数差异显著；对于断奶仔猪数（LSW）而言，F=7.96，P=0.001 1 <0.05，说明不同杂交组合母猪的断奶仔猪数差异显著。

图4.7　同一因素对不同指标单因素方差分析SAS 程序

图4.8　同一因素对不同指标单因素方差分析SAS 程序输出结果

2.多重比较

（1）不同组合产仔数（LS）的多重比较

多重比较结果表明（图4.9），大白猪×八眉猪（B）组合母猪的产仔数为12.50 头，显著高于其他3 个组合（P<0.05），而其他3 个组合母猪的产仔数差异不显著（P>0.05）。

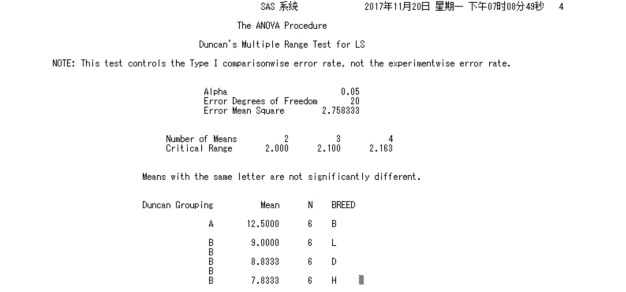
图4.9　杂交品种因素对LS 单因素方差分析多重比较SAS 程序输出结果

（2）不同组合断奶仔猪数（LSW）的多重比较

多重比较结果表明（图4.10），大白猪×八眉猪（B）组合母猪的断奶仔猪数为11.83，显著高于其他3 个组合（P<0.05），而其他3 组显著高于其他3 个组合（P <0.05），而其他3 个组合母猪的产仔数差异不显著（P>0.05）。

图4.10　杂交品种因素对LSW 单因素方差分析多重比较SAS 程序输出结果

在所分析的4 个二元杂交组合中，从产仔数和断奶仔猪数两个性状的分析结果来看，以大白猪×八眉猪组合的母猪最好，其他3 个组合虽然在这两个性状上表现有一定差异，但差异不显著（P>0.05）。

（3）各个处理重复数不等的单因素试验资料的方差分析

各个处理重复数不等的单因素试验资料方差分析与各个处理重复数相等的单因素试验资料的方差分析步骤相同，所不同的是：

①各项平方和与自由度的计算公式略有不同。

②采用LSD 或LSR 法进行多重比较，需计算各个处理的平均重复数以计算均数差数标准误或均数标准误。

例4.3　5 个不同品种猪的育肥试验后期30 d 增重（kg）列于表4.3，检验5 个品种猪育肥试验后期30 d 增重有无差异？

表4.3　5 个品种猪育肥试验后期30 d 增重

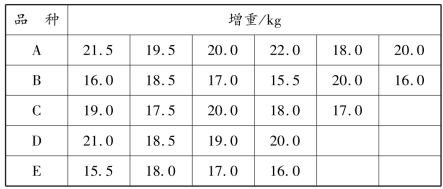
这是一个处理重复数不等的单因素试验资料，处理数k=5，各个处理重复数n1=6，n2=6，n3=5，n4=4，n5=4，试验观测值总个数N=25，其SAS 分析程序如图4.11 所示。

图4.11　各个处理重复数不等的单因素试验资料的方差分析SAS 程序

图4.11 所示为各个处理重复数不等的单因素试验资料的方差分析SAS 程序，PROC GLM过程为调用GLM 过程（即最小二乘分析）；CLASS BREED 指明BREED（品种）为分类变量（即以品种为分组的依据）；MODEL GAIN= BREED 指明模型为单因素主效应模型；LSMEANS BREED/STDERR TDIFF 用于计算各效应的最小二乘均数（LSM），其选项可用于进行不同处理（效应）最小二乘均数间的差异显著性检验（即多重比较）。常用选项包括STDERR（最小二乘均数的标准误）、TDIFF（均数差异显著性检验的t 值）、ALPHA=α（显著性检验的显著性水平），默认的显著水平（α=0.05）。

输出结果如图4.12 所示。

1.方差分析过程

该部分是输出PROC GLM 进行方差分析的过程。与PROC ANOVA 过程不同，GLM 过程可按4 种不同的方法计算各因素所引起的离均差的平方和（只需在MODEL 语句之后加入选项/SS1 SS2 SS3 SS4）。在不设定假设检验的输出结果时，系统会自动输出各因素所引起的Ⅰ型（TypeⅠSS）及Ⅲ型离均差平方和（Type ⅢSS）。对于均衡资料而言，GLM 过程计算的4 种平方和是相同的，对于非均衡资料而言，通常选用Ⅲ型平方和的结果。本例中方差分析的结果，F=5.99，P=0.002 5 <0.05，表明不同品种猪育肥试验后期30 d 增重差异显著。

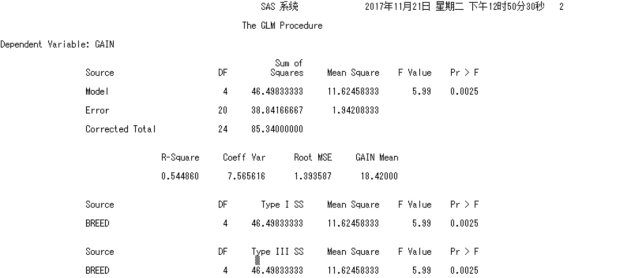
图4.12　各个处理重复数不等的单因素试验资料的方差分析过程SAS 结果

2.多重比较

该部分对不同处理均数间的差异显著性在规定的显著性水平上进行多重比较。最小二乘的SAS 统计分析中多重比较结果采用的是三角形表示法。各组最小二乘均数列为一排，第二排为两组比较的P 值。本例中，由结果可知，品种A 和品种B、品种A 和品种E、品种D 和品种E 日增重差异极显著（P <0.01），品种A 和品种C，品种B 和品种D 日增重差异显著（0.01 <P<0.05），其余两两比较差异不显著（P>0.05）。

其SAS 程序如图4.13 所示。

图4.13　各个处理重复数不等的单因素试验资料的多重比较过程SAS 结果

（二）两因素试验资料的方差分析

两因素水平组合方式有交叉分组和系统分析两种，因而两因素试验资料的方差分析分为两因素交叉分组试验资料的方差分析和两因素系统分组试验资料的方差分析两种。

（1）两因素交叉分组试验资料的方差分析

对于交叉分组资料的多个因素来源，某一因素的每个处理（水平）与另一个因素的每个处理（水平）都可以自由组合，且都要碰到（即交叉），所有因素处于完全平等的地位。但每一因素各个处理的组合内可以有一个观察值（无重复）或多个观察值（有重复）。根据不同因素间是否有互作，还可以分为无互作和有互作的多因素方差分析。

①两因素无互作交叉分组试验资料的方差分析。

两因素（A、B）无互作的方差分析数学模型为：

Yij=μ+ai+bj+eij

式中，Yij为观察值；μ 为总体平均数；ai为A 因素第i 个处理效应，bj为B 因素第j 个处理效应，eij为随机误差，服从N（0，σ2）分布。

例4.4　为研究雌激素对大白鼠子宫发育的影响，从4 个不同品系各1 窝未成年的大白鼠中选3 只体重相近的雌鼠，随机分别注射3 种剂量的雌激素，然后在相同条件下饲养至成年，称得它们的子宫质量列于表4.4，对试验资料进行方差分析。

表4.4　4 个品系大白鼠注射不同剂量雌激素的子宫质量

这是另一个因素交叉分组单个观测值试验资料，A 因素（品系）有4 个水平，即a=4；B 因素（雌激素注射剂量）有3 个水平，即b=3；共有N=a ×b=12 个观测值，其SAS 分析程序如图4.14 所示。

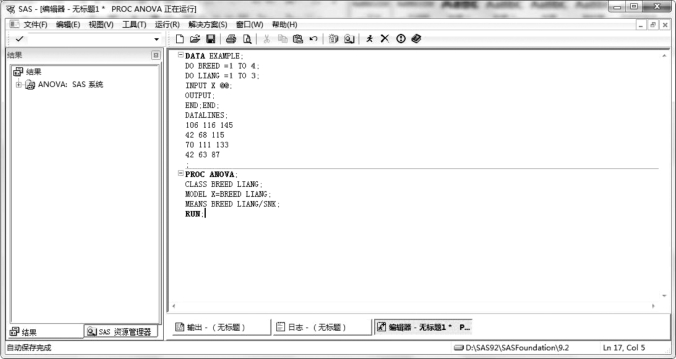
图4.14　两因素无互作交叉分组试验资料的方差分析SAS 程序

图4.14 所示为两因素无互作交叉分组试验资料的方差分析SAS 程序，PROC ANOVA 过程为调用ANOVA 过程（即方差分析）；CLASS BREED LIANG 指明为BREED（品系）、LIANG（剂量）为分类变量；MODEL X=BREED LIANG 指明两因素无互作的方差分析模型（主效应模型）；MEANS BREED LIANG/SNK 用Q 值法作为多重比较的方法，默认的显著水平（α=0.05），此过程中若用DUNCAN 法作为多重比较，则需要标注MEANS BREED LIANG/DUNCAN，同理，用LSD 法作为多重比较，则需要标注MEANS BREED LIANG/LSD，若以α=0.01 作为显著检验水平，则需要在多重比较方法后标注MEANS BREED LIANG/SNK ALPHA=0.01。

输出结果如图4.15 所示。

图4.15　两因素无互作交叉分组试验资料的方差分析过程

（1）方差分析过程

方差分析的结果，就不同品系大白鼠子宫质量影响而言，F=23.77，P=0.001 <0.05，表明品系不同对大白鼠子宫质量差异影响显著；就不同剂量对大白鼠子宫质量影响而言，F=33.54，P=0.000 6 <0.05，表明剂量不同对大白鼠子宫质量差异影响显著。因此，说明假设的模型很好地解释了观察数据（P=0.000 4，R2=0.958 445），或者说，否定H0，接受HA。

（2）多重比较

①不同品系。采用Q 值法进行多重比较的结果表明，品系A1和A3大白鼠子宫质量显著高于品系A2和A4（P<0.05），品系A1和A3及品系A2和A4大白鼠之间子宫质量差异不显著（P>0.05）。4 个品系大白鼠子宫质量高低顺序依次为：A1>A3>A2>A4。

SAS 程序如图4.16 所示。

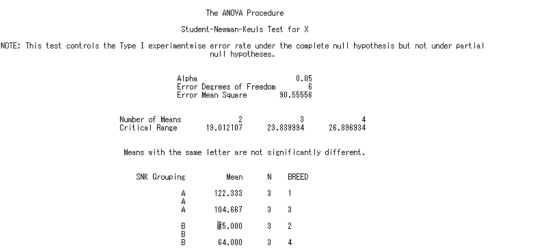
图4.16　品系间多重比较SAS 程序运行结果

②不同剂量。采用Q 值法进行多重比较的结果表明，剂量B3下大白鼠子宫质量显著高于剂量B2下大白鼠子宫质量（P<0.05），剂量B3下大白鼠子宫质量显著高于剂量B1下大白鼠子宫质量（P <0.05），剂量B2下大白鼠子宫质量显著高于剂量B1下大白鼠子宫质量（P<0.05）。

SAS 程序如图4.17 所示。

图4.17　剂量间多重比较SAS 程序运行结果

例4.5　用3 种能量相同、蛋白质水平不同的饲料对2 个品种各6 头猪进行育肥对比试验，记录了育肥期的日增重（GAIN）和活体背膘厚度（BACKFAT）两个性状，具体数据见表

4.5，假设饲料效应和品种效应之间无互作，试比较不同饲料和品种在两个性状上是否存在显著差异。其SAS 程序如图4.18 所示。

表4.5　2 个品种猪饲喂不同蛋白质含量饲料的增重和背膘厚度

(www.xing528.com)

图4.18　2 个品种猪饲喂不同蛋白质含量饲料的增重和背膘厚度SAS 程序

图4.18 所示为两因素无互作交叉分组有重复观测值试验资料的方差分析SAS 程序，采用DUNCAN 法作为多重比较的方法，默认的显著水平（α=0.05）。本试验中，同时比较两个因素对两个变量的方差分析（即2 个两因素无互作有重复观测值方差分析同时比较）。

输出结果如图4.19 所示。

1.方差分析过程

①不同饲料和品种对增重的影响。方差分析结果显示，不同饲料的影响，F=5.32，P=0.010 1 <0.05，表明不同饲料和品种对增重的影响差异显著；不同品种的影响，F=25.54，P=0.000 1 <0.05，表明不同饲料和品种对增重的影响差异显著。

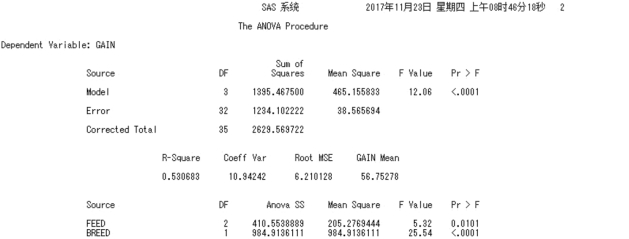
图4.19　2 个品种猪饲喂不同蛋白质含量饲料的增重方差分析结果

②不同饲料和品种对背膘厚度的影响。方差分析结果显示，不同饲料的影响，F=1.30，P=0.286 8 >0.05，表明不同饲料和品种对背膘厚度的影响差异不显著；不同品种的影响，F=29.95，P=0.000 1 <0.05，表明不同饲料和品种对背膘厚度的影响差异显著。

SAS 程序如图4.20 所示。

图4.20　2 个品种猪饲喂不同蛋白质含量饲料的背膘厚度方差分析结果

2.多重比较结果

①不同饲料对增重和背膘厚度的影响。采用SSR 法在α=0.05 水平下进行多重比较表明，饲料因素对增重的影响：第一种饲料显著高于第二种、第三种饲料（P<0.05），第二种饲料和第三种饲料差异不显著（P>0.05）。3 种不同饲料对背膘厚度影响差异不显著（P>0.05）。

SAS 程序如图4.21 所示。

图4.21　不同蛋白质含量饲料对增重和背膘厚度影响的多重比较结果

②不同品种对增重和背膘厚度的影响。采用SSR 法在α=0.05 水平下进行多重比较表明，品种因素对增重的影响：第一个品种显著高于第二个品种（P <0.05）。品种因素对背膘厚度的影响：第一个品种显著高于第二个品种（P<0.05）。

SAS 程序如图4.22 所示。

②两因素有互作交叉分组试验资料的方差分析。

进行多因素试验时，除了研究每一个因素对试验指标的影响外，往往更希望研究试验因素之间的交互作用，如通过对畜禽生长发育所需饲量的能量、蛋白、脂肪、氨基酸及微量元素等对畜禽生长发育的影响有无交互作用的研究，对最终确定有利于畜禽生长发育的最佳饲粮配方是有重要意义的。

前面介绍的两因素单个观测值试验只适用于两个因素无交互作用的情况，若两个因素有交互作用，每个水平组合只实施在1 个试验单位，即每个水平组合只有1 次重复，只有1 个观测值的试验设计是不正确或不完善的，因为：

a.若A、B 两因素有交互作用，Xij=μ+ai+bj+ξij，SST=SSA+SSB+SSe，dfT=dfA+dfB+dfe中SSe和dfe实际上是A、B 两因素交互作用和误差的平方和与自由度，MSe是交互作用和误差均方，主要反映交互作用和误差引起的变异，这时若仍按原来的方法进行方差分析，由于MSe为交互作用和误差的均方，有可能掩盖试验因素各水平平均数差异的显著性，从而增加犯Ⅱ型错误的概率。

图4.22　不同品种对增重和背膘厚度影响的多重比较结果

b.每个水平组合只实施在1 个试验单位上，即每个水平组合只有1 次重复，只有1 个观测值，无法正确估计试验误差，不可能研究因素的交互作用，进行多因素试验时，一般应设3个或3 个以上重复，才能正确估计试验误差。

两因素有交互作用的方差分析数学模型为：

Yijk=μ+ai+bj+aj×bj+eijk

式中，Yijk为观察值；μ 为总体平均数；ai为A 因素第i 个处理的处理效应，bj为B 因素第j 个处理的处理效应；aj×bj为A 因素第i 个处理与B 因素第j 个处理的互作效应；eijk为随机误差，服从N（0，）分布。

例4.6　为研究饲料中钙、磷含量对仔猪生长发育的影响，将饲料中的钙含量（A）分为3个水平、磷含量（B）分为4 个水平，交叉分组，共有3 ×4=12 个水平组合，每个水平组合重复3 次。选用品种、性别、日龄相同，初始条件基本一致的仔猪36 头，随机分成12 组，每组3 头，用能量、蛋白质含量相同的饲料在钙、磷含量搭配下各喂一组仔猪，经2 个月试验，仔猪增重数值列于表4.6，分析钙、磷含量对仔猪增重的影响。

表4.6　不同钙、磷含量（%）对仔猪增重的影响（kg）

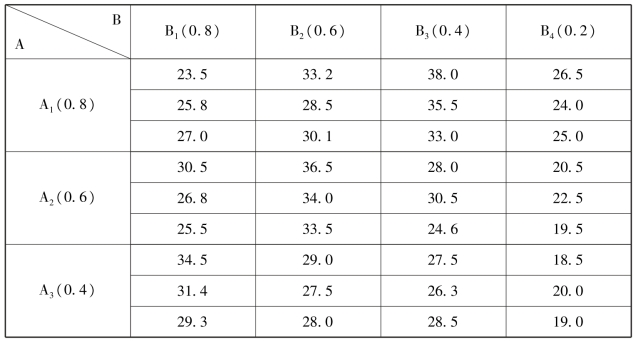
这是一个两因素交叉分组有重复观测值试验资料，A 因素（钙含量）有3 个水平，即a=3，B 因素（磷含量）有4 个水平，即b=4；交叉分组，共有ab=3 ×4=12 个水平组合；每个水平组合的重复数n=3；试验共有abn=3 ×4 ×3=36 个观测值，两因素有互作模型方差分析采用的PROC GLM 模型进行程序编写，SAS 程序如图4.23 所示。

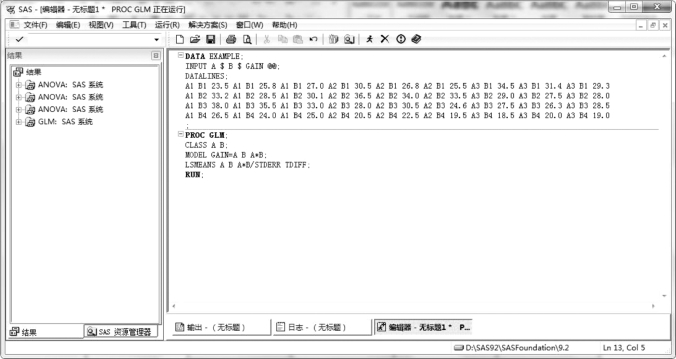
图4.23　两因素有互作方差分析SAS 程序

输出结果为：

1.方差分析过程

方差分析结果表明，钙含量（A）对仔猪增重情况影响，F=5.09，P=0.014 3 <0.05，表明饲料中不同钙含量对仔猪增重影响差异显著；磷含量（B）对仔猪增重情况影响，F=42.05，P<0.000 1，表明饲料中不同磷含量对仔猪增重影响差异显著；钙含量和磷含量交互作用（A×B）对仔猪增重情况影响，F=11.67，P<0.000 1，表明饲料中不同钙、磷含量的交互作用对仔猪增重影响差异显著。

两因素有互作模型方差分析F 检验结果如图4.24 所示。

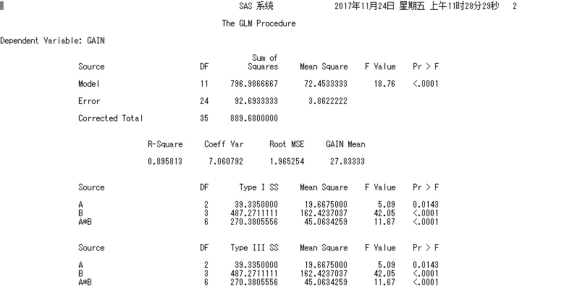
图4.24　两因素有互作模型方差分析F 检验结果

2.多重比较结果

由于A 因素、B 因素和A×B 因素F 检验结果差异均显著，故对其进行多重比较，多重比较结果如下：

①钙含量（A）各水平对仔猪增重的多重比较：A1和A3水平钙含量对仔猪增重效果对比显示其效果影响差异显著（P<0.05），A1和A2、A2和A3水平钙含量对仔猪增重影响差异不显著（P>0.05）。饲料含量以A1水平钙含量对仔猪增重效果较好（仔猪平均增重最大）。

SAS 程序如图4.25 所示。

图4.25　钙含量（A）各水平对仔猪增重的多重比较

②磷含量（B）各水平对仔猪增重的多重比较：B2和B4、B3和B4、B1和B4、B2和B1水平磷含量对仔猪增重效果对比显示其效果影响差异显著（P <0.05），B2和B3、B3和B1水平磷含量对仔猪增重效果对比显示其效果影响差异不显著（P >0.05）。饲料含量以B2水平磷含量对仔猪增重效果较好（仔猪平均增重最大）。

SAS 程序如图4.26 所示。

③各水平组合仔猪平均增重的多重比较，由图4.27 可知，各水平组合仔猪平均增重两两比较，第一行为最小二乘均值，第二行为两两比较的概率值，P<0.05 即差异显著，P>0.05 即差异不显著。试验结果在此不再赘述。

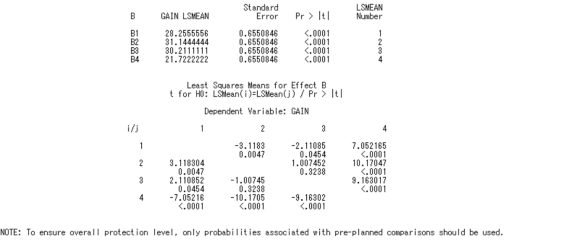
图4.26　磷含量（B）各水平对仔猪增重的多重比较

图4.27　各水平组合仔猪平均增重的多重比较

（2）两因素系统分组试验资料的方差分析

在多个因素组成水平组合时，先将A 因素分为a 个水平，再在Ai（i=1，2，…，a）下，将B因素分为b 个水平，记为Bij（j=1，2，…，b），然后在Bij下将C 因素分为c 个水平，记为Cijl（l=1，2，…，c），这样得到的多个因素水平组合的方式称为系统分组或多层分组、套设计、窝设计。

按系统分组方式组成多个因素的水平组合，首先划分水平的因素为一级因素，其次划分水平的因素为二级因素，然后划分水平的因素为三级因素，……

两个因素按系统分组方式组成的水平组合，二级因素的各水平套在一级因素的每个水平下，它们之间是从属关系，而非平等关系。两因素系统分组侧重分析一级因素。

按系统分组方式组成的多个因素水平组合进行试验得到的资料称为多因素系统分组试验资料，根据样本含量是否相等，多因素系统分组试验资料分为次级样本含量相等和不相等两种类别。

在畜牧育种试验中，系统分组是一种常用的实验设计。即先按A 因素的水平数分组，再按B 因素的水平数分组，互不交叉。系统分组二因素方差分析的数学模型为：

Yijl=μ+ai+bij+eijl

式中，Yijl为A 因素第i 个水平与B 因素第j 个水平的观测值；μ 为总体平均数；ai为A 因素第i个处理效应；bij为A 因素第i 个水平下B 因素第j 个处理效应；eijl为随机误差，服从N（0，）分布。

在应用SAS 程序进行两因素系统分组资料的分析时，其相应的效应模型为嵌套效应模型。

①次级样本含量相等的两因素系统分组试验资料的方差分析。

例4.7　为测定3 种鱼粉A1，A2，A3的蛋白质消化率，在不含蛋白质的饲料里按一定的比例分别加入3 种鱼粉配制成饲料，各饲喂3 头试验动物Bi1，Bi2，Bi3（i=1，2，3）。收集排泄物，风干，粉碎，混合均匀。分别从每头试验动物的排泄物中各取两份样品作化学分析。消化率测定结果列于表4.7，分析3 种鱼粉的蛋白质消化率是否有差异？

表4.7　3 种鱼粉的蛋白质消化率

这是一个次级样本含量相等的两因素系统分组试验资料，一级因素A 为鱼粉，水平数a=3；二级因素B 为试验动物，水平数b=3；Bij有2 个观测值，即n=2；共有abn=3 ×3 ×2=18 个观测值。其SAS 程序如图4.28 所示。

图4.28　次级样本含量相等的两因素系统分组试验资料的方差分析SAS 程序

图4.28 所示为次级样本含量相等的两因素系统分组试验资料的方差分析SAS 程序，采用Q 值法作为多重比较的方法，默认的显著水平（α=0.05）。本程序中，采用的MOEDL DIGESTIBILITY=A B（A）的嵌套效应模型，A 为一级因素，B 为在A 作用下的二级因素。TEST H=A E=B（A）过程指明检验A 效应时以B（A）作为误差项；MEANS A/SNK E=B（A）指明以B（A）作为误差项对A 效应做多重比较。

输出结果如图4.29 所示。

1.方差分析过程

在输出结果中，鱼粉因素效应的F 值和相应的P 值有两个，由于在程序中已经指定了对A 效应进行检验时以B（A）作为误差项，因而在结果分析时，应选以B（A）作为误差项的结果。本例中方差分析的结果，A 效应（鱼粉因素效应）的影响（F=12.43，P=0.007 3 <0.05）差异显著；A 效应内B 效应（即鱼粉因素影响下试验动物效应，F=27.57，P<0.000 1）的差异显著。

图4.29　次级样本含量相等的两因素系统分组试验资料的方差分析结果

2.多重比较结果

采用Q 值法进行多重比较，结果表明，A2、A1鱼粉蛋白质平均消化率显著高于A3鱼粉（P<0.05），A1和A2鱼粉蛋白质平均消化率差异不显著（P>0.05）。

SAS 程序如图4.30 所示。

图4.30　次级样本含量相等的两因素系统分组试验资料的多重比较结果

②次级样本含量不等的两因素系统分组试验资料的方差分析。

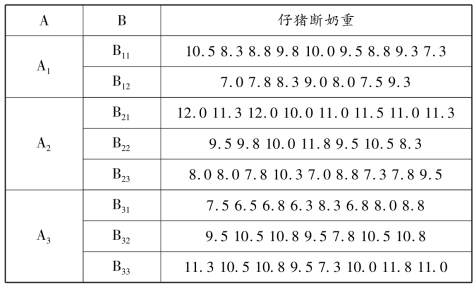
例4.8　某品种3 头公猪配8 头母猪所产63 头仔猪的35 日龄断奶重（kg）列于表4.8，分析不同公猪与不同母猪的仔猪断奶重是否有差异？

表4.8　3 头公猪配8 头母猪所产63 头仔猪断奶重

这是一个次级样本含量不等的两因素系统分组试验资料，一级因素A 为公猪，水平数a=3；二级因素B 为所配母猪，bi（i=1，2，3）为第i 头公猪所配母猪数，为母猪总数；nij为第i 头公猪与所配第j 头母猪所产的仔猪数，以及Bij的重复数；为第i 头公猪的仔猪数，即Ai的重复数；N=63 为仔猪总数，即试验观测值总个数。其SAS 程序如图4.31 所示。

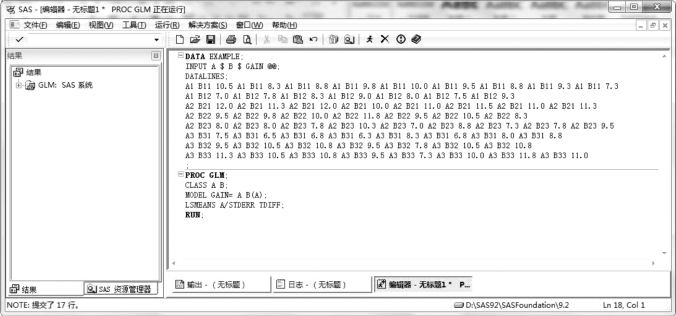
图4.31　次级样本含量不等的两因素系统分组试验资料的方差分析SAS 程序

输出结果如图4.32 所示。

1.方差分析过程

方差分析的结果表明，不同公猪因素（A 因素）对仔猪断奶体重的影响（F=6.56，P=0.002 8 <0.05）影响差异显著；A 因素影响下不同母猪因素（B 因素）对仔猪断奶体重（F=15.74，P<0.000 1）的影响差异显著。

图4.32　次级样本含量不等的两因素系统分组试验资料的方差分析结果

2.最小二乘均数及其差异显著性检验

A1、A2、A33 个品种公猪后代仔猪断奶体重的最小二乘均数（标准误）分别为8.64（0.26），9.82（0.21），9.18（0.21）。多重结果表明，3 个品种公猪后代仔猪断奶体重：A2显著高于A1（P<0.05），A2显著低于A3（P <0.05），A1和A3差异不显著。其中以A2品种最好，A3品种次之，A1品种最低。

次级样本含量不等的两因素系统分组试验资料的多重比较结果如图4.33 所示。

图4.33　次级样本含量不等的两因素系统分组试验资料的多重比较结果