极限的定义与求解方法-中学数学教师

“极限”这一常考点的考查方式有两种：一是利用两个重要极限和洛必达法则来求极限并根据极限的定义来进行验证；二是根据迫敛性等函数极限的性质来求解或证明极限.

1.极限的定义

定义1 设｛an｝为一个数列，若=a，a为有限常数，则称数列｛an｝收敛，反之，称数列｛an｝为发散的.

极限的定义（ε-N语言）：=a⇔∀ε＞0，存在N ∈N+，对于∀n＞N都有＜ε成立，则称an→a.

注：数列极限存在与数列收敛等价.

定义2 设f（x）为定义在实数域上的函数，A为有限常数，若∀ε＞0，存在N＞0，对于∀x，当＞N时，有＜ε成立，则称A为函数f（x）在x→∞的极限，记作f（x）=A.

注：.

定义3 设f（x）在 x0的某个去心邻域 U °（x0，δ′）内有定义，A为有限常数，若∀ε＞0，存在 δ＞0（δ＜δ ′），对 于∀x ∈{x：0＜＜δ}，有＜ε成立，则称A为函数f（x）在 x→x0时的极限，记作f（x）=A.

注：.

2.两个重要极限

第一个重要极限；第二个重要极限或者.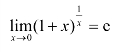

3.洛必达法则(www.xing528.com)

洛必达法则是指利用导数来研究未定式极限的一种方法，它是处理未定式极限非常有效的手段.但它只能直接用于型或型的不定式，而对于0·∞，∞0，00，1∞及∞-∞型的未定式必须通过变形化成型或型的未定式后才可以利用洛必达法则.

洛必达法则Ⅰ（型）

设函数f（x）和g（x）满足f（x）=0，g（x）=0，在点a的某个去心邻域内 f′（x）和 g′（x）均存在（g′（x）≠0），且=A（A∈R），则有

洛必达法则Ⅱ（型）

设函数 f（x）和 g（x）满足，在点a的某个去心邻域内f′（x）和g′（x）均存在（g′（x）≠0），且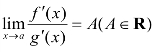，则有

4.等价无穷小

无穷小量是以0为极限的函数，不同的无穷小量收敛于0的速度有快有慢，若 x→x0时，f（x）和g（x）均为无穷小量，且，则称f（x）与g（x）是 x→x0时的等价无穷小，记作 f（x）～g（x）.

设函数f（x），g（x），h（x）在U°（x0）内有定义，且 f（x）～g（x）（x→x0），则以下结论成立：

（1）若f（x）h（x）=A，则g（x）h（x）=A.

（2）若=B，则=　B.