高中数据分析教材内容解析

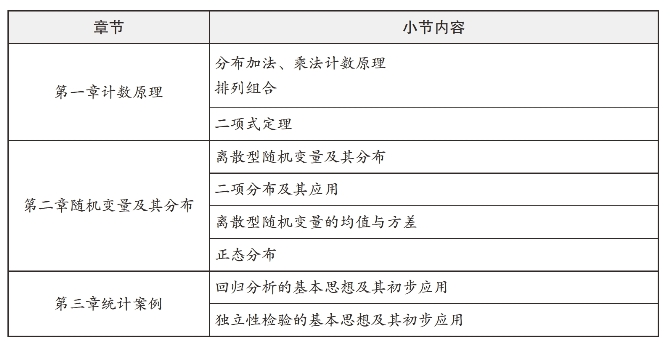
高中数据分析内容（以人教版为依据）主要设置在必修三（见表7-1）、选修1-2、选修2-3（见表7-2）三部分。在初中学生已经简单学习了收集数据、整理数据的方法，利用平均数、中位数等样本估计总体，体会数据的随机性。在必修三中将在此基础上进一步学习收集、整理、描述数据的方法，如分层抽样，以及体会变量间的相互关系和概率知识的进一步学习。在选修内容中，由于学生已经学习了概率知识，这部分学生将进一步学习离散型随机变量及其分布，利用离散型随机变量思想描述和分析某些随机事件，解决实际问题。通过对典型案例回归分析、独立性检验的基本思想及其初步应用，进一步研究了两个变量的关系，通过散点图直观地了解两个变量的关系，然后通过最小二乘法建立回归模型，最后通过计算相关指数评价模型的好坏。如果模型比较好地刻画了两个变量的关系，对应自变量值，就可以通过模型预测结果。具体教材内容分布见表7-1与表7-2。

表7-1　必修三数据分析相关知识点表

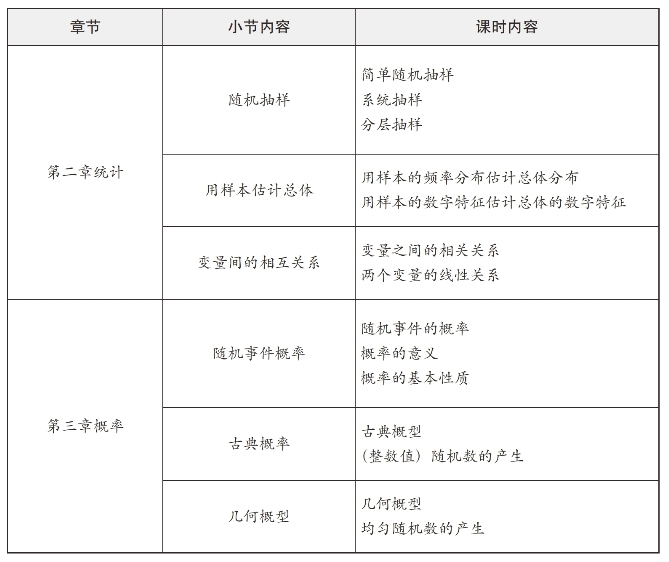
表7-2　选修2-3数据分析相关知识点表

（一）教材内容分类分析

数据分析过程主要包括收集数据、整理数据、提取数据、构建数据、进行推理、获得结论。数据分析主要表现为：收集和整理数据，理解和处理数据，获得和解释结论，概括和形成知识。依据课标以及参考其他相关论文，笔者将高中数据分析能力分为数据整理、数据计算、数据描述、数据解释、数据推理五个部分。将高中教材内容归类见表7-3。

表7-3　高中数据分析知识点归类表

上述归类只是将最突出表现的特征加以归类，部分内容存在知识间的联系，如用样本的数字特征估计总体的数字特征，其中涉及平均数、众数、中位数、标准差等知识，就包含着数据计算，但是这部分最突出的教学目标应该是利用数据统计量来描述数据的一些特点，所以将其列在数据描述分类中。同时，在解释生活中一些实际问题时，如为什么体育竞技中，要将评委的分数去掉最低分和最高分，再取平均数，这也是考查学生对数据统计量的理解。所以，本书将用样本的数字特征估计总体的数字特征同时放在了数据解释部分。

（二）教材内容分类理论基础

在上面分类分析的基础上，又对数据整理、数据计算、数据描述、数据解释、数据推理五部分在高中教材中的主要原理公式进行了分类整理，以便为后续的研究提供理论依据。

1.数据计算理论基础

排列：从n个不同元素中取出m（m≤n）个元素的所有不同排列的个数叫作从n个不同元素中取出m个元素的排列数。

组合：从n个不同元素中取出m（m≤n）个元素的所有不同组合的个数，叫作从n个不同元素中取出m个元素的组合数。

离散型随机变量：对于随机变量可能取的值，可以按一定次序一一列出，这样的随机变量叫作离散型随机变量。(www.xing528.com)

连续型随机变量：对于随机变量可能取的值，可以取某一区间内的一切值，这样的变量就叫作连续型随机变量。

古典概型：试验中所有可能出现的基本事件只有有限个，每个基本事件出现可能性相等，我们将具有这两个特点的概率模型称为古典概率模型。

几何概型：如果每个事件发生的概率只与构成该区域的长度（面积或体积）成比例，则称这样的概型为几何概型，简称为几何概型。

2.数据整理理论基础

简单随机抽样：一般地，设一个总体含有N个个体，从中逐个不放回地抽取n个个体作为样本（n≤N），如果每次抽取时，总体内的各个个体被抽到的机会都相等，就把这种抽样方法叫作简单随机抽样。

系统抽样：一般地，假设要从容量为N的总体中抽取容量为n的样本，我们可以按下列步骤进行系统抽样：先将总体的N个个体编号，有时可直接利用个体自身所带的号码，确定分段间隔k，对编号进行分段N/n（n是样本容量）是整数时，取k=N/n，在第1段用简单随机抽样确定第一个个体编号l（l≤k），按照一定的规则抽取样本，通常是l加上间隔k得到第2个个体编号（1+k），再加得到第3个个体编号（l+2k），依次进行下去，直到获取整个样本。

分层抽样：一般地，在抽样时，将总体分成互不交叉的层，然后按照一定的比例，从各层独立地抽取一定数量的个体，将各层抽取的个体合在一起作为样本，这种抽样方法是一种分层抽样。

必修三用样本的频率分布估计总体分布，其中介绍了三种方法，即频率分布直方图、频率分布折线图、茎叶图。

3.数据描述、解释理论基础

在初中就已经学习过众数、中位数、平均数的概念，这些数字能够提供关于样本数据的特征信息，如何在频率直方图中估计中位数、众数、平均数就是高中进行学习的，下面将逐一进行介绍。

中位数：在样本中，有50%的个体小于或等于中位数，也有50%的个体大于或等于中位数。因此，在频率直方图中，中位数左边和右边的直方图的面积应该是相等，由此可以估计中位数的值。

平均数：平均数的估计值等于频率直方图中每个小矩形的面积乘以小矩形底边中点横坐标之和。

众数：在频率分布直方图中最高的那个。

标准差：考查样本数据分散程度的大小，最常用的统计量是标准差。标准差是样本到平均数的一种平均距离，一般用s表示。

4.数据推理理论基础

回归直线：通过收集的数据画出散点图，如果散点图中点的分布从整体上看大致是在一条直线附近，我们就称这两个变量之间具有线性相关关系，这条直线叫作回归直线。如果能够求出这条回归直线的方程（简称回归方程），就可以了解变量间的相关性。