二、在数学解题教学中培养学生直观想象素养的策略

（一）将数学问题“图形化”

在数学解题教学中教师应该倡导借助图形理解题目的方法，图形很多时候都比数学符号更容易让学生接受。一旦学生养成利用图形求解问题的习惯，那么在以后的学习过程中就可以逐步提高自己的直观想象素养。在解决数学问题之前，首先要对数学问题有一定的理解，也就是将数学问题进行表征。但表征的方式并不是唯一的，每一种表征会产生不同的解题方法，所以经常会出现一题多解的情况。对普通高中数学课程中几何直观的解题表征形式进行了总结，大概可以分为以下三种：直观示意图、几何图形、函数图像。

1.解题教学中的直观示意图表征

直观示意图是为了将复杂的文字表述转化为形象简明的图形。在解题的过程中，直观的图形表述会对我们理解题意有很大的帮助。直观示意图也有很多的表征形式，在高中数学中常用的有线段示意图、树状图、Venn图、图表等表征形式。

2.解题教学中的几何图形表征

在解决数学问题的过程中很多时候是需要利用图形辅助的，图形辅助的方式也是多种多样，有的需要画出平面图形，有的需要画出立体图形，但最终的目的都是为了可以更好地解决问题。当遇到这一类的问题时，学生本身是可以意识到需要图形辅助解决，但并不能很好地把握借助哪一种图形辅助，教师应该在恰当的时机进行引导。在这样的解题过程中，可以培养学生构建与数学符号相对应的图形的思维，提高学生的直观想象素养。

3.解题教学中的函数图像表征

函数是伴随我们整个高中数学课程的知识点，在整个高中数学中无处不在，是高中数学学习的重点，同样也是难点。如果教师将函数作为一般的概念课对学生进行讲授，那么学生必然无法理解，因为函数的教学是需要图像去辅助的。只有通过函数图像直观地演示函数的性质以及变化，才可以让学生从本质上理解函数。教师应该注重函数的作图，让学生在解决函数问题的过程中更好地运用函数图像。

（二）将直观图形“最佳化”

在数学学习中，图形表达远比数字符号更受欢迎。在解决数学问题的时候，我们更愿意将抽象的数字符号变成更容易理解的图形，这样可以更加直观方便地得到解决问题的思路。但要画出恰当的可以解决问题的图形也并非易事，因为差之毫厘，谬以千里。在题目的解决过程中需要学生理解题意，依据题意画出与之对应的图形，只有合适的图形才可以更好地解决问题。因此，依据题意画出合适的图形是解决问题的重点，而构造这样的图形要从以下两个方面考虑。(www.xing528.com)

1.恰当的图形视角

在解决几何问题的过程中，构造图形可以从不同角度进行，但是不同角度的图形会形成不同的直观分析。如果我们根据题意画出的图形不能很好地反映所要解决的问题，那可能还会影响我们的解题效率。例如，我们在解关于立体几何的相关试题时，有的题目是没有图形的，需要我们自己构造。比如，某题目中要求绘制三棱柱，那么学生可能绘制图6-4中的两种形式。

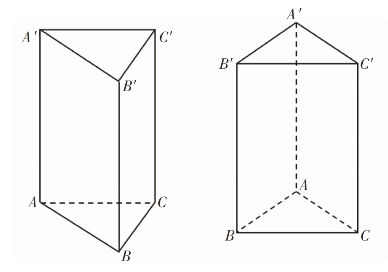
图6-4　三棱柱

以上的两种形式都是正确的，但是在实际运用中哪一种更加方便有效呢？从不同的角度所观察到的信息是不同的，教师可以要求学生讲述自己为什么要从这个角度去画图，然后教师本人讲述其他角度的画图思维，彼此对照得到最适合题目的图形。在探究的过程中，学生可以更快地掌握画图的诀窍。

2.构造正确的图形

每个题目都有各自对于图形的要求，有的题目需要我们根据题意画出比较精确的图形。比如，在题目中给出圆的半径、直线的长度、两条直线平行或者直角三角形等条件，在这样的题目中就需要我们构造比较精确的图形。而有的题目就可以根据题意画出大概的图形即可。比如，在判断直线与圆的位置关系时，重点展示的是直线与圆的位置关系，而与它们的大小无关，这个时候就只需要画出大概的示意图即可。对于此类数学问题，教师应该留给学生一定的时间进行分组讨论与交流，自我分析所作图形的可行性，经过反思，最终画出适合题目的准确图形。通过这样的过程，培养学生直观分析的能力，提升学生的直观想象素养。

（三）将识图能力“全面化”

利用直观想象素养解决数学问题，不仅需要通过图形得到题目中的有用信息，而且也需要学生提高识别图形的能力，对整体的图形有一个全面的认识，从图形中的已知信息向着结论进行直观的推理，探索出解决问题的思路。

在解决数学问题的过程中，构建合适的图形会让我们更快且更准确地找到解决问题的思路。若是通过题目中给出的公式，我们无法直观地得到解题思路，那么我们需要将抽象的公式转化为形象的图形，从而找到解决问题的思路。在整个过程中，重点是将图形完整全面地构建出来，这样才能准确直观地找到解题思路。