在新授课教学中培养学生直观想象素养的策略

直观想象素养在数学新知识的学习中有着非常重要的作用，在高中数学中有很多的知识点讲解都需要运用直观想象素养。比如，立体几何中直线与圆的位置关系判定，需要利用图形来直观地表达直线与圆的三种位置关系；在函数中，需要借助函数图像来直观地演示函数的性质。在高中数学课堂中讲授这些知识点都需要借助直观想象素养，去提高学生对于知识本质的理解。在教学的过程中，学生跟随教师，将运用直观想象素养的经验方法进行总结，提升自己的综合能力。直观想象素养并不是可以直接灌输给学生的知识，培养学生的直观想象素养需要通过教学去完成。因此，如果教师可以在课堂中创设合适的问题情境，设计学习活动等，将直观想象素养的养成渗透到日常教学中，那么对于学生直观想象素养的培养肯定大有好处。

（一）联系生活，抽象数学问题

数学源于生活，生活中处处可见数学。学习数学的目的在于可以将之运用于生活实际，解决生活中的实际问题。历史上著名的哥尼斯堡七桥问题中讲到，哥尼斯堡市内的一条河有两个小岛，连接这两个小岛的有一座桥，连接两岸与两岛的还有六座桥，一共七座桥，如图6-1所示，要求得出一次走完七座桥并且每座桥都只走一次的路径。

图6-1　哥尼斯堡七桥问题

联系生活实际，将问题从实际情境中抽象出来，用数学的形式表达出来。把两个岛作为点，河的两岸也是点，那么桥就是连接这些点的线。每边的河岸都与其中的一个岛之间有两座桥连接，那么也就是作为河岸的点与作为其中一个岛的点有两条线段连接，另一个岛与两岸分别只有一座桥，所以连线就只有两条，两个岛之间也是一条连线。

关于七桥问题，图6-1中A、B、C、D分别代表两个小岛以及河的两岸，然后我们就可以将问题转化为从A、B、C、D某一点出发，经过七条线并且每条线只经过一次的路线。联系生活，抽象数学问题，是我们解决生活实际问题的重要方式。

案例1：某地区一锅炉房发生爆炸，在锅炉房外一条笔直的道路上有一辆运送水果的货车要将水果运到仓库中，突然在广播中听到锅炉房爆炸的消息，而爆炸的中心点位于货车正西80km处，锅炉房爆炸形成的爆炸区域是半径长为50km的圆形区域。已知仓库位于爆炸中心正北60km处，如果这辆货车不改变前进的方向，货车会受到爆炸的影响吗？通过联系生活，我们可以想象爆炸会形成一个圆形区域，而货车行走的则是一条直线，要判断货车会不会受到爆炸的影响，就是看货车前进形成的直线会不会遭遇到爆炸形成的圆，那么用数学的语言进行描述的话，就是判断直线与圆的位置关系。经过计算，可以得到货车形成的直线与爆炸形成的圆相交了。所以，如果货车不改变前进的方向，会受到爆炸的影响。

（二）结合图形，推导数学问题

“几何与代数”的内容阐述中有这么一句：“通过几何图形建立直观，通过代数公式表达规律。”从中可以看出，几何图形对于我们建立直观想象有非常重要的作用。很多的数学问题，单纯地依靠公式或定理去解决，实际上并不是最优的解决方法，我们可以结合图形去思考问题，这样可以从图形中直观地想象解决问题的思路。(www.xing528.com)

通过分析案例1中的材料，我们可以结合生活实际，将该问题转化为直线与圆的位置关系的判定问题。解决此类问题，结合图形可以让我们更加直观地得到解决问题的思路。我们可以将爆炸中心作为原点O，以东西方向为x轴，建立直角坐标系，A为货车，B为仓库，如图6-2所示，其中取10km为长度单位。

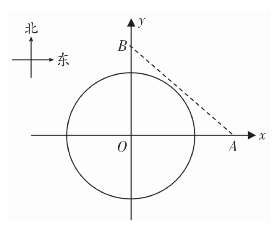
图6-2　坐标系

由此可知，爆炸影响的圆形区域的圆心O坐标为（0，0），圆的半径为5，A点的坐标为（8，0），B点的坐标为（0，6），根据以上数据可以得到爆炸影响的圆形区域所对应的圆的方程为x2+y2=25，货车前行形成的直线的方程为3x+4y=24，联立直线与圆的方程得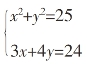，消去y，可得25x2-144x+176=0，因为Δ=1442-4×25×176＞0，所以直线与圆相交。由此得出结论：如果货车不改变前进方向，会受到爆炸的影响。

（三）应用多媒体，直观数学问题

随着科学技术水平的提高，人们的生活有了很大的改变，越来越便利。在这同时，科技的力量也开始在教育中慢慢体现，最直观的就是课堂教学的改变，教师不再局限于粉笔加黑板的授课方式，也开始运用新颖的信息技术进行授课。不得不说，在数学中有关直观想象的知识点讲授中我们是需要这样的方式的。借助多媒体技术，我们可以在大屏幕上为学生直观地演示数学问题的思考发展过程，让学生更好地理解所学的知识点。

案例1是普通高中课程标准试验教科书A版必修2第四章“圆与方程”中第二节第一课时的探究问题，我们在课前通过这样的情境引导学生回忆直线与圆的位置关系判定。而我们在初中知识的学习中就已经知道直线与圆有三种位置关系，即相交、相切、相离，那么具体的演示是怎么样的呢？接下来，教师就利用多媒体直观地为学生演示直线与圆三种位置关系的变化过程。

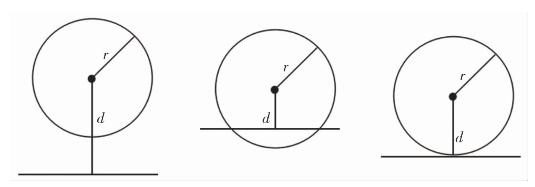
图6-3　位置关系

我们在多媒体中将直线到圆心的距离d与圆的半径r进行了详细的对比。如图6-3所示，在多媒体中，首先直线l在圆O的下方，与圆O相离，这个时候圆心到直线的距离d大于圆的半径r。接着，在多媒体中将直线l向圆心方向平移到直线l与圆相切，这个时候圆心到直线的距离等于圆的半径。最后，将直线l继续向上平移，这个时候直线与圆相交，可以看出圆心到直线的距离d小于圆的半径r。那么，直线与圆的位置关系就可以通过圆心到直线的距离与半径的大小进行判断。利用题中已知条件，以爆炸中心为原点O，以东西方向为x轴，建立直角坐标系，A为货车，B为仓库，则爆炸影响的圆形区域的圆心O坐标为（0，0），圆的半径为5，A点的坐标为（8，0），B点的坐标为（0，6），根据以上数据可以得到爆炸影响的圆形区域所对应的圆的方程为x2+y2=25，货车所在的直线的方程为3x+4y=24，则圆心到直线的距离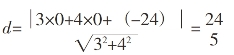，则d＜r，所以直线与圆相交。由此得出结论：如果货车不改变前进方向，会受到爆炸的影响。