多载波微放电全局“最坏状态”

多载波微放电全局“最坏状态”是LMD和SMD所有阈值中更低者对应的相位组合。在LMD情况下，“最坏状态”Φi的多载波信号能够诱发电子数处于“临界状态”，该功率可视为LMD阈值。在SMD情况下，虽然每一个Tx窗口的“最坏状态”Φi可以基于式（5－12）来优化获得，但对所有Tx窗口进行分析比较时，需要一个与“临界状态”类似的依据来确定全局“最坏状态”Φi。

在实际中，是否发生多载波微放电是由是否能够被高灵敏度测试系统探测到来决定。从这个意义上来说，对于各种微放电都存在一个“可检测阈值”，包括SMD［6］。为了将该阈值与每个Tx窗口的“最坏状态”Φi联系起来，本节分析了测试系统检测灵敏度与NEmax之间的关系。

在电磁学中，充满电子的真空空间可看作等离子体媒质，其等离子频率由空间电子密度Ne确定［7］：

式中，－e和me分别为电子的电量和质量。

该媒质的等效介电常数为：

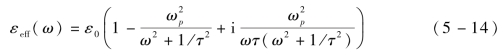
式中，τ＝μeme／e为电子的散射时间［8］；μe为等离子体媒质中电子的迁移率。

当电磁波传播通过一个厚度为L的平板状的等离子体媒质时，如图5－3所示，反射系数可以表示为：

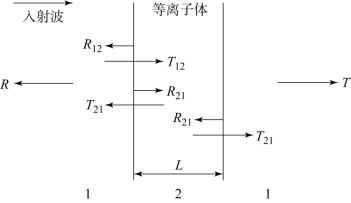
图5－3　电子分布区域等效媒质的散射特性分析模型

(www.xing528.com)

式中，

值得注意的是，大部分微放电发生在由平行的或同轴的金属结构构成的空间，因此式（5－15）适用于多种微波部件。

式（5－15）将微波部件的传输特性和电子密度明确地联系在一起。Ne取0对应于真空，意味着0反射。随着Ne的增加，ωp也相应增加。当ωp接近于微波部件的工作频率，使得由εeff（ω）引发的反射系数的变化足够大以至于能够被测试系统的最小灵敏度检测到，此时对应的电子密度可认为是可检测微放电的“阈值密度”［9］。

图5－4给出了采用式（5－15）计算的随电子密度逐渐增长时反射系数的变化。在计算中，等离子体媒质的厚度设为1 cm，电子的迁移率μe取10 000 m2／（V·s）［8］。从图中可以看出，当电子密度在106～1011／cm3变化时，反射系数在－100～0 dB这一很宽的范围内变化。特别是，如果微放电可以被具有－70 dB灵敏度的系统检测到，那么在UHF频段，二次电子的密度应该大于107／cm3。因此，一旦给定微放电测试系统的灵敏度，就可以获得这一反射对应的“阈值密度”。该“阈值密度”可以进一步与阈值NEmax联系起来。对于均匀分布的空间电子，阈值NEmax可以通过阈值密度和电子占据的体积相乘获得；对于非均匀分布的电子，等效体积可以通过观察电子在部件中的分布来估计，阈值NEmax可以通过阈值密度和等效体积相乘获得，而电子的空间分布可以通过粒子模拟获得。

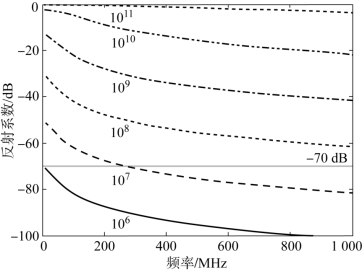
图5－4　反射系数随电子密度的变化

到目前为止，本节建立了式（5－12）中优化目标NEmax与测试系统灵敏度的联系，对于给定的N0、PSC和阈值NEmax，单个包络周期微放电“最坏状态”Φi、对应的Tx窗口以及SMD阈值均可通过一个迭代优化获得。在引入阈值NEmax的概念后，式（5－12）改进为：

基于式（5－16）优化获得SMD全局“最坏状态”的流程如图5－5所示，对本节提出的扫描电子渡越时间与临界电子密度相结合的方法，能否找到满足全局优化条件的最短Tx窗口最为重要。式（5－12）也可以用来优化局部极小值，这一简化将不会给全局优化带来任何误差。

图5－5　单个包络周期微放电“最坏状态”全局优化流程图

需要说明的是，本节基于等离子体媒质模型给出的“阈值密度”可直接应用于矩形波导、同轴传输线等二维结构，结合粒子模拟可以推广应用于复杂结构微波部件“阈值电子密度”的计算。