多载波微放电快速计算介绍

为了说明如何建立多载波信号与单载波信号对应的电子增长率之间的联系，基于文献［29］提出的非稳态统计理论对间隙为0.43 mm的理想平板结构进行了空间电子数随时间变化的计算，如图4－13所示。采用频率为3.77 GHz、上下极板电压从95 V到120 V变化的单载波信号作为激励。可以看出，经过很短时间的过渡后，在对数坐标下空间电子数呈线性增长，同时具有小幅暂态波动。这反映了在单载波微放电过程中电子数目是随时间指数增长或减小的事实。小幅暂态波动是由连续正弦信号的加速或减速周期引起的，其与单载波信号具有相同的频率。

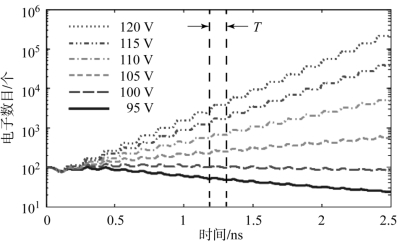
图4－13　单载波微放电演化过程中二次电子数目的周期性波动

针对其线性变化曲线，可以定义电子增长速率（Growth Rate，GR）为：

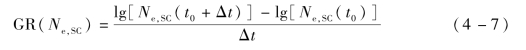
式中，Ne，SC为图4－13中的一条曲线，代表特定激励电压单载波信号作用下电子数随时间的变化曲线。图4－14给出了基于图4－13曲线和式（4－7）计算的电子增长速率曲线。该曲线形状和SEY模型的相似，意味着这两者存在内在联系：该曲线上的每个点与每个单载波信号的幅度对应，零增长速率对应的是电子数目处于平稳状态的临界阈值，即单载波微放电阈值，为100.94 V；当激励电压小于该阈值时，增长速率小于0，即电子数目随时间降低；当激励电压大于该阈值时，增长速率大于0，即电子数目随时间增长，但当激励电压为某一特定值时存在最大增长速率，这与二次电子发射系数存在最大值密切相关，而当电压高于该临界值时，增长速率反而降低。

图4－14　二次电子数目的增长速率随单载波信号输入功率的关系曲线

在实际微波部件中，由于电场非均匀分布导致的电子横向扩散使得空间电子数随时间的变化变为准线性，文献［33］分析了由于矩形波导的非均匀电场导致的二次电子横向扩散，从而导致其二次电子数量的增长呈现准线性。图4－15给出了长和高分别为58.17 mm和0.43 mm的矩形波导在长边中点处高度方向的积分电压从100 V到125 V时变化时的电子数随时间的变化曲线。从图中可以看出，较理想平行平板结构，其电子数增长呈现了准线性特性。实际工程中，大多数微波部件的电场分布是非均匀的。在这种情况下，当微波部件受单载波信号激励时，在对数标尺下，二次电子数目将随时间近似线性增长或降低。

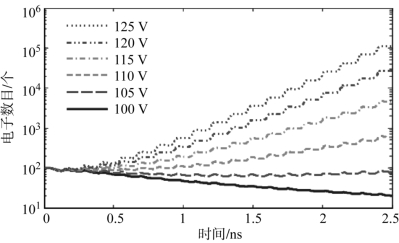
图4－15　单载波信号激励下TE10模式工作的矩形波导中二次电子数目的周期性波动，波导的横截面尺寸为58.17 mm×0.43 mm

针对这一情况，定义电子平均增长速率（Average Growth Rate，AGR）为：

式中，Ne，SC代表特定激励电压下电子数随时间的变化曲线，描述了给定幅度时空间电子数随时间变化的特性；Δt为半正弦的持续时间。

理想平行平板的电子增长速率可通过对式（4－8）取N＝1获得。后面针对同轴传输线和波导阻抗变换器均采用式（4－8）的平均电子增长速率曲线进行计算。

借助获得的电子数增长速率曲线，由多载波信号激发的空间电子数随时间变化可以立即计算获得。对于多载波信号的每个类半正弦信号，等效正弦信号的幅度可以通过式（4－4）计算，与该部分多载波信号对应的空间电子增长特性可以通过将对应的等效幅度置于增长速率曲线上查询获得。采用这种方式，所有连续多载波信号作用下的空间电子数随时间变化可以通过如下迭代过程计算获得：

式中，Δt和Ne，MC（i）分别为单载波信号的持续时间和第i次多载波信号累积后的电子数量；Ccal为用来补偿计算获得的AGR曲线潜在误差的校正系数。因为二次电子发射和吸收是两个不同的物理过程，Ccal对应正、负电子增长的取值不同，因此将其分别表示为Chigh和Clow。

为了获得校正系数Chigh和Clow，可以选择两个分别具有正、负平均增长速率的电子数随时间变化曲线，并通过式（4－9）来计算。然后，可以用计算曲线来匹配采用商业粒子模拟工具模拟的曲线，以获得最优的校正系数。采用最小二乘法来优化获得Chigh和Clow。

优化的目标函数为：

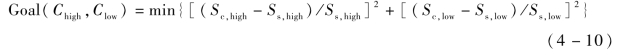
式中，Sc和Ss分别为计算和模拟获得的电子数随时间变化曲线的平均增长速率；下标high和low分别代表具有正、负平均增长速率的曲线。

接下来将具体介绍如何在实际同轴传输线中基于式（4－8）～式（4－10）快速计算空间电子数随时间变化曲线。增长速率曲线采用基于CST模拟单载波微放电的结果计算获得，同时获得的电子数随时间变化曲线将和模拟结果进行比对。在模拟中，采用的6路多载波信号的中心频率和频率间隔分别为340 MHz和10 MHz，相对带宽为15%。

本节仍选用4.2节中的同轴传输线模型，选择CST提供的银的Furman二次电子发射模型。图4－16（a）给出了对频率为340 MHz的单载波信号进行功率扫描的模拟结果。当输入功率为200.4 W时，增长速率约为0，对应单载波微放电阈值功率。在对数坐标下，经过一个很短时间的过渡期后，所有模拟曲线随着时间线性增加或减小。基于图4－16（a）可以获得增长速率曲线，如图4－16（b）所示。增长速率曲线的总体形状与SEY模型曲线相似，基于式（4－10），对该部件而言，校正系数Chigh和Clow分别为0.75和0.9，在计算和模拟中采用的多载波信号的配置如表4－3所示。其中采用三角相位多载波信号的模拟结果来匹配以获得校正系数。一旦获得校正系数，任何相位组合多载波信号的空间电子数随时间变化曲线可以通过式（4－9）直接计算获得。采用相同的Dell服务器，对于每种相位组合的多载波信号进行粒子模拟耗时12～15 h，而采用本书所提出方法只耗时6 ms。

图4－16　所选同轴传输线微波部件340 MHz单载波信号作用时粒子模拟结果

（a）不同输入功率的二次电子数目变化；（b）电子增长速率曲线

表4－3　6载波信号的频率和相位组合参数列表

图4－17～图4－19分别给出了同相相位分布［0，0，0，0，0，0］、三角相位分布［0，68.67，137.33，137.33，68.67，0］和一种特定相位分布［0，75，150，150，75，0］三种典型多载波信号的电子数目演化计算和模拟的结果。为了比对，采用两种相位组合分别对空间电子数随时间增加或减少两种情况进行计算和模拟。如上面讨论的，空间电子数随时间变化的临界状态在估计多个包络周期微放电阈值时更为重要，因此选择了临界状态附近的电子数随时间变化情形，即具有较小的增长或降低平均增长速率的情况进行分析。对于所有情形，相同的校正系数适用于三种波形，计算获得的电子数随时间变化曲线与多载波微放电粒子模拟获得的曲线符合良好。最重要的是，空间电子数随时间变化的计算时间减少到毫秒量级，使得通过遍历或多维优化获得“最坏状态”及全局阈值成为可能。

图4－17　同轴传输线同相相位条件下模拟结果和本书所提出方法的比较

（a）载波功率34.4 W；（b）载波功率24.5 W

图4－18　同轴传输线三角相位条件下模拟结果和本书所提出方法的比较

（a）载波功率32.0 W

图4－18　同轴传输线三角相位条件下模拟结果和本书所提出方法的比较（续）

（b）载波功率29.6 W

图4－19　同轴传输线相位［0，75，150，150，75，0］条件下模拟结果和本书所提出方法的比较

（a）载波功率36.1 W；（b）载波功率29.6 W

为了定量评估计算结果和模拟结果之间的误差，进行一阶多项式拟合，从而获得电子数目随时间的平均增长速率，结果如表4－4所示。从表中可以看出，在各种情况下，计算结果和模拟结果之间的误差均很小。(www.xing528.com)

表4－4　同轴传输线模拟结果和计算结果的比较

接下来给出了具有复杂结构和非均匀场分布的实际微波部件的计算结果，所提出方法同样适用。所选微波部件为矩形波导阻抗变换器。图4－20给出了阻抗变换器的粒子模拟模型。该部件工作在Ku频段，中心频率为12 GHz。部件的最窄间隙为0.42 mm，整个部件宽19.05 mm，长32 mm。

图4－20　波导阻抗变换器模型

根据以上给出的步骤，首先模拟了不同功率单载波信号激励条件下二次电子数目随时间的变化，模拟结果如图4－21所示。在模拟中，单载波信号的频率选为12 GHz，功率从0.5 W到31 250 W进行了扫描。从模拟结果可以看出，单载波微放电阈值约为2 112.5 W。与图4－16（a）相比，可以看出图4－21中模拟曲线的稳态区域在对数标尺下具有微弱的非线性。由前面的分析可知，这是由矩形波导横截面电场非均匀分布引起的。与图4－15类似，平均增长速率随时间略微增加，特别是对低能量的单载波信号。这种情况下，根据不同时间点的曲线斜率计算获得的增长速率曲线会略有不同。

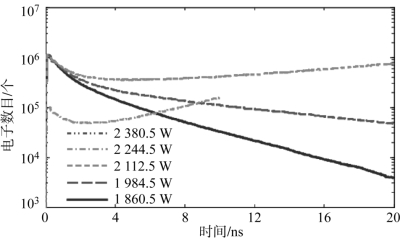
图4－21　矩形波导阻抗变换器不同输入功率的二次电子数目变化

图4－22给出了基于不同时刻的二次电子增长曲线获得的电子增长速率。从图中可以看出，在低能量部分其增长速率受所选时刻的影响显著。为了说明这一问题，图4－23给出了基于不同时间模拟曲线计算获得的增长速率曲线。从图中可以看出，对于低能量的单载波信号，由于初始电子的扩散效应，在模拟开始的短时间内（4 ns以内），新产生的二次电子在数量上未占多数，因此电子增长率随时间变化，但是在该过渡时间之后，二次电子的增长呈现稳态。同时可以看出，当功率增加至3 000 W以上时，该过渡效应的影响几乎消失。这里对低能量段的增长速率采用4.25 ns以后的稳态结果。

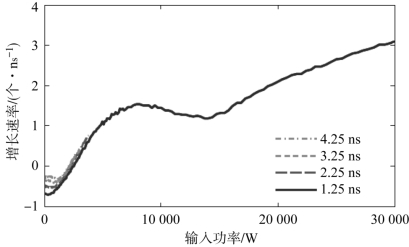
图4－22　基于1.25～4.25 ns模拟数据的平均增长速率曲线

图4－23　低输入功率时增长速率曲线

为了验证所提出方法的有效性，以电子数目变化稳态以后曲线建立其平均增长速率曲线，所选8路载波信号的频率分别为11.744 GHz、11.820 6 GHz、11.897 2 GHz、11.973 8 GHz、12.050 4 GHz、12.127 GHz、12.203 6 GHz和12.280 2 GHz，采用式（4－10）获得校正系数Chigh和Clow，对于电子数目随时间增长的部分校正系数Chigh为0.85，对于电子数目随时间降低的部分校正系数Clow为1.3。这里同样采用三角相位分布的多载波信号的粒子模拟结果进行匹配。

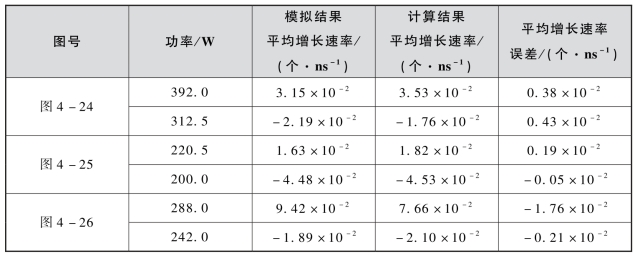
图4－24～图4－26分别给出了三种多载波信号激励的二次电子数随时间变化曲线计算结果与模拟结果的比较。从图中可以看出，两者总体趋势吻合良好。三种信号的初始相位分别为同相相位分布［0，0，0，0，0，0，0，0］、三角相位［0，51.175，102.35，153.525，153.525，102.35，51.175，0］和一种特定的相位组合［0，75，150，300，300，150，75，0］。表4－5给出了电子数随时间的平均增长速率误差估计。从表中可以看出，基于所提出方法计算获得的曲线与粒子模拟获得曲线吻合良好。这进一步证明了所提出方法同样适用于复杂结构微波部件的多载波微放电阈值计算。

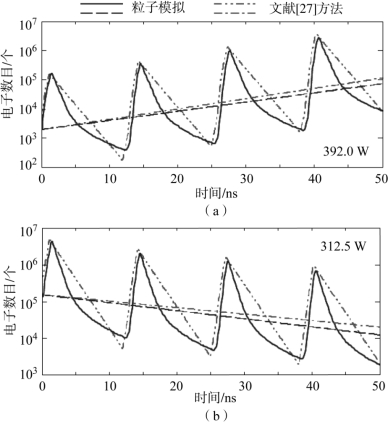
图4－24　矩形波导阻抗变换器同相相位条件下模拟结果和本书所提出方法的比较

（a）载波功率392.0 W；（b）载波功率312.5 W

图4－25　矩形波导阻抗变换器三角相位条件下模拟结果和本书所提出方法的比较

（a）载波功率220.5 W；（b）载波功率200.0 W

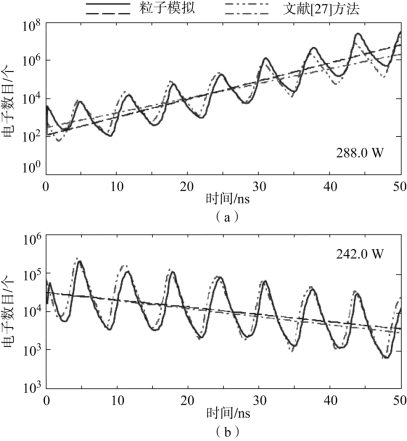
图4－26　波导阻抗变换器相位［0，75，150，300，300，150，75，0］条件下模拟结果和本书所提出方法比较

（a）载波功率288.0 W；（b）载波功率242.0 W

表4－5　矩形波导阻抗变换器模拟结果和计算结果的比较

基于以上验证可以看出，基于所提出的等效单载波近似方法，计算给定多载波信号作用下的电子数随时间变化所用的时间显著减少，因此所提方法有效解决了多载波微放电阈值高效计算这一技术难题。对于给定的微波部件，只要获得了该部件的二次电子增长速率曲线，并通过典型相位的模拟曲线进行匹配校正，就可以快速计算任何配置多载波信号激励时的二次电子数随时间变化曲线，载波数及相邻载波之间的频率间隔均可任意给定。只是当微波部件的内部结构修改后，电子增长速率曲线才需要重新建立。

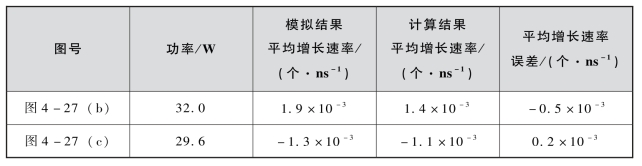
为了获得微波部件的电子增长速率曲线，选择合适的单载波信号进行功率扫描是关键。在以上验证中，单载波信号的频率选择为多载波信号的中心频率。实际上，基于二次电子发射模型的频率无关特性，该频率可以在多载波信号带宽内自由选择。图4－27（a）给出了图4－1所示同轴传输线工作频率分别为340 MHz和346 MHz的电子数增长速率曲线。从图中可以看出，虽然两个频率对应的电子增长速率曲线明显不同，但基于346 MHz的电子增长速率曲线计算获得的电子数目随时间变化曲线与模拟结果同样吻合良好，如图4－27（b）、（c）所示。两种功率条件下的电子数目随时间平均增长速率如表4－6所示。从表中可以看出，计算结果和模拟结果之间的误差均很小。

图4－27　基于不同频率单载波粒子模拟结果获得的电子增长速率曲线及其计算结果比较

（a）增长速率曲线；（b）载波功率32.0 W时模拟结果和本书所提出方法的比较；（c）载波功率29.6 W时模拟结果和本书所提出方法的比较

表4－6　计算结果与模拟结果的比较

通过将两个相邻零点间的多载波信号等效为幅度经过调整的单载波信号，可进一步改善加速作用的等效，在适用于任意复杂结构微波部件的同时，可将计算时间降低到毫秒量级。但是，作为一种等效方法，误差是不可避免的。如上面提到的，非均匀电场分布能够导致对数坐标下电子数增长呈准线性，这在计算AGR时将引入误差。因为增长速率曲线是在单载波信号的稳态激励下获得的，对宽带多载波信号，由包络的突然变化引起的瞬态响应将引入较大误差。对于连续的低能量包络，非稳态吸收过程也将引入误差。由于多载波微放电是大尺度随机过程，对于提出方法进行误差和适用性的严格分析是非常困难的。在这种情况下，对不同带宽和相位分布进行校正系数的验证是一条可行途径。

对于相同的同轴传输线，本节进一步分析了同相和三角相位分布时频率间隔分别为15 MHz、20 MHz和25 MHz时的校正系数。相应的相对带宽分别为22%、29%、37%，获得的电子数增长如图4－28所示。从图中可以看出，相同的校正系数Chigh和Clow对22%带宽的两种波形均适用；对于29%带宽，相同的Chigh和Clow也适用，但是对于同相相位的正增长情况误差变大；37%带宽也表现出类似的趋势。这与瞬态误差分析是一致的：在不同相位的波形中，同相分布多载波信号具有最快的瞬态包络变化。

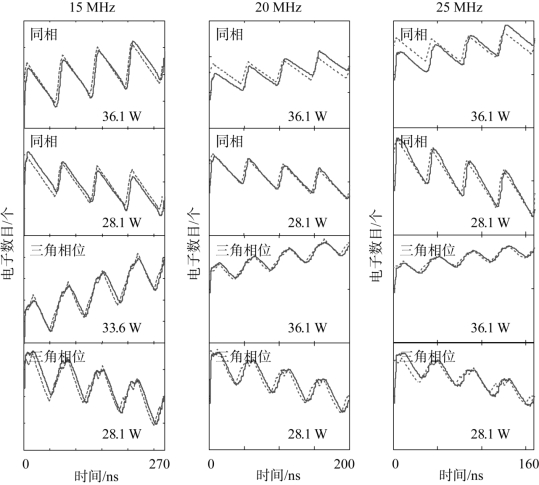
图4－28　频率间隔分别15 MHz、20 MHz和25 MHz时电子数模拟（实线）与计算（虚线）结果比对

图4－29给出了不同频率间隔的校正系数Chigh和Clow，随着频率间隔的增加，Chigh和Clow均减小，同时Chigh的值始终比Clow低。注意到Chigh和Clow是1时，对应着电子数增长的计算结果和模拟结果在不需要任何校正的情况下误差为零。因此，图4－29意味着随着带宽的增加，未校正的电子数增长的计算结果误差增大，同时低能量包络导致的负增长的误差比高能量导致的正增长的误差小，这与之前的分析一致。对于每种频率间隔，校正系数可以适用于不同波形的信号，但是对于新的频率间隔，校正系数则需要重新计算。

图4－29　校正系数随频率间隔增加的变化

在本节中，电子数增长速率是基于粒子模拟结果获得，对于简单结构的微波部件也可以根据文献［29，34］中提出的解析方法进行单载波微放电的功率扫描。在多载波微放电粒子模拟中，为了清楚地观察到多载波信号激励时二次电子随时间变化的趋势，需要模拟多个包络周期，其中二次电子的总数目可能会非常大，甚至达108以上。因此，这种模拟通常非常耗时，并且需要大量的计算空间。由于微波部件的复杂性，单条模拟曲线通常需要几小时到十几个小时。相比较而言，为了获得单载波正弦信号电子数增长速率，只需对单载波的几个射频周期进行模拟，这种单载波微放电的模拟相对于数个多载波包络周期的模拟而言耗时显著减少。因此，单载波信号的功率扫描所需的时间要少很多。更重要的是，在完成了功率扫描之后，多载波信号激励时电子数随时间变化曲线的计算可在毫秒量级时间内完成。

将快速计算获得的电子数随时间变化曲线与模拟曲线进行了比对，结果显示，两者吻合良好，因此该方法的精度与所用粒子模拟工具的精度相同。通过采用所提出方法，计算多载波微放电二次电子数目随时间变化所需的时间可以减少到毫秒量级，基于该方法能够进一步实现在整个相位空间中挑选出能以最低阈值激发多载波微放电的“最坏状态”相位组合。