多载波微放电的等效单载波近似方法

多载波微放电阈值分析的本质是从所有相位组合中挑出能够以最低功率激发微放电的相位组合，即“最坏状态”。为了实现上述目标，需在多载波所有可能的相位组合中确定“最坏状态”对应的全局极值点［20］。如2.3节所述，初始相位组合的数量极其庞大。在如此海量的相位组合中进行“最坏状态”相位组合的全局搜索，必须解决多载波条件下电子数随时间变化的快速计算问题。迄今，针对实际复杂结构微波部件内部电子数随时间变化分析的唯一方法是通过粒子模拟进行［21－26］。对于空间典型微波部件和指定初始相位组合的多载波信号，其微放电粒子模拟时间可介于数小时至数十小时，因此完全不具备进行“最坏状态”相位组合全局搜索的现实可行性。为了解决上述问题，本节在单载波微放电分析的基础上，提出了等效单载波近似方法，将多载波信号作用下电子的加速过程通过幅度相应调整后的单载波信号来等效，显著减少了获得特定相位组合多载波信号微放电阈值的时间，使得通过遍历或优化实现“最坏状态”确定能够得以实现。

本书1.2节中给出了常用的两种描述二次电子发射的物理模型。可以看出，初始电子撞击金属表面产生的二次电子的数目只依赖于电子能量或者入射速度，与加速电场的频率无关。上述频率无关性用于推导能够高效率地计算电子数随时间变化的等效单载波近似方法。

通过观察图2－1（a）给出的具有8个载波的同相初始相位分布的多载波合成信号的时域波形可以看出，合成多载波信号总是可以看作一系列连续的通过零点的信号组成，任意两个零点之间的部分类似于半周期的正弦信号。将上述两个零点之间的“类半正弦信号”示于图4－12（a），并设其持续时间为τ1，幅度为E1。同时，另设一真正的半周期正弦信号（即半周期单载波信号），其持续时间为T／2。T为单载波信号对应的周期，幅度为E2。

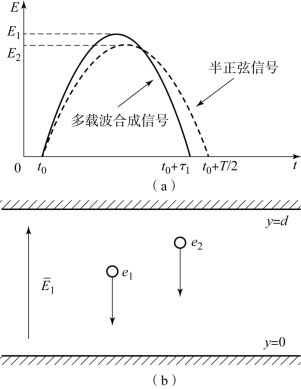
图4－12　电子加速类半正弦等效原理分析［27］

（a）两零点之间的类半正弦信号；（b）分析模型

对金属平行平板两极板之间的电子在上述两种信号电场作用下的加速效应进行分析，设平行平板的间隙为d，时间t0～t0＋τ1的多载波信号激发的电场E1（t）对电子e1进行加速，如图4－12（b）所示［27］。

在等效单载波近似分析中，设实际电子e1和等效电子e2具有相同的初速度，为了公式表述简洁，初速度均取0；同时图4－12（a）中的多载波信号和半正弦单载波信号均以t0时刻为起始点，因此，后面以t0时刻为局部时间的起点进行推导。在时间τ1之后，电子e1沿着－y方向被加速至瞬时速度：

式中，－e和m分别为电子的电量和质量。同时，e1的位移为：

因此，如果e1的初始位置为y＝－d1（τ1），电子将以mv21（τ1）／2的能量撞击到下极板，根据1.2节给出的二次电子发射模型可以获得该次撞击的二次电子发射系数。(www.xing528.com)

根据式（4－1），在时间τ1内电子e1的加速只依赖于电场E1（t）对时间τ1的积分，即电场E1（t）和时间t轴围起来的面积。这意味着如果该类半正弦信号被具有相同积分的真正半正弦信号代替，总是会找到能够产生相同SEY的电子e2。将真正半正弦信号表示为E2（t）＝E2 sin（2πt／T）。其中，E2为半正弦信号的幅度，T为单载波正弦信号的周期，为使其积分面积与“类半正弦信号”相等，E2需满足：

即：

经过时间T／2，一个静止的电子e2被E2 sin（2πt／T）的单载波信号加速至瞬时速度：

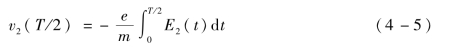
该速度恒等于v1（τ1），因此具有同样初始速度和不同初始位置－d2（τ2）的电子e2，将会以同样的能量mv21（τ1）／2撞击下极板，因此会产生与e1相同的二次电子。其中，

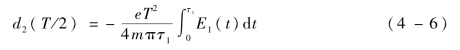
根据该等效单载波近似分析，为了产生相同的二次电子，任一类半正弦信号对电子的加速作用可以等效为幅度由式（4－4）确定的真正半周期正弦信号对电子的加速。这也意味着在连续类半正弦多载波信号作用下的电子数增长可以通过一系列严格半正弦信号的电子增长速率的来估计，其中每个半正弦信号的幅度分别由式（4－4）确定，而同一频率不同幅度的单载波正弦信号作用下电子的增长速率可以采用已有的成熟理论和粒子模拟方法来确定［21－26］。

在上述推导过程中，电子e1和等效电子e2的初始速度相同，多载波信号和等效单载波半正弦信号的起始加速时刻也相同，唯一不同的是电子e1的位置距离下极板为－d1，等效电子e2的位置距离下极板为－d2。而已有理论表明，微放电是一个由巨量空间二次电子构成的复杂动态随机过程［28，29］，其中二次电子的出射速度和角度分别服从麦克斯韦分布和余弦分布［30］，且与加速电场的频率无关，使得微放电过程中微波部件内部的二次电子沿电场方向的分布呈完全随机的状态。同时文献［31］的模拟结果表明，在微放电开始时，二次电子沿电场方向形成了平行于金属表面的共振薄片，而当电子数增加到足够多时，该共振薄片会展宽，最终充满两金属板之间的空间，使得在垂直于电场的不同平面内电子的统计特性近似相同。因此，根据以上分析，当微波部件中的二次电子数量足够大时，在多载波合成信号不同的类半周期，电子的初始位置虽然略有改变，但在统计上与实际位置近似相符。所以，这种等效在电子数目足够大时经过适当的校准其计算精度是可以接受的。

根据以上等效单载波近似方法，对微放电而言，原合成多载波信号可以等效地由一系列幅度满足式（4－4）的半周期单载波正弦信号代替，且由上述信号加速的大量电子具有相同的二次电子产出。通过以上等效，多载波微放电过程中电子数随时间变化可等效地由幅度经过调整的单载波信号并结合单载波微放电的二次电子累积速率进行计算。由于单载波微放电的理论与模拟已经非常高效和成熟，上述方法可以极大地加速多载波微放电过程中电子数随时间变化的计算速度。其计算步骤如下：①采用理论或模拟方法得到不同功率单载波（其频率可取多载波信号的中心频率）微放电过程中的二次电子累积速率，建立单载波功率与二次电子增长速率之间一一对应的查找表曲线；②设定多载波微放电分析的初始电子数目，采用式（4－4）逐次获取每个“类半正弦信号”的等效单载波信号幅度，通过查找表曲线获得对应幅度单载波信号的二次电子增长速率，实现多载波微放电过程中二次电子数量随时间变化的累积计算。

通过以上方法，在获得单载波信号的电子增长速率查找表曲线之后可以将多载波微放电过程中电子数随时间变化过程的计算时间由粒子模拟所需的十几小时大幅减少到毫秒量级［27，32］，使得在大量相位组合中采用遍历或优化方法进行多载波微放电“最坏状态”分析成为可能。