同相相位分布多载波微放电粒子模拟

多载波微放电的演化过程与单载波存在显著差异，多载波信号受初始相位的影响，其合成信号的幅度在很大范围内变化。如忽略带宽的影响，在高于单载波微放电阈值的高功率持续时间满足二次电子倍增条件，电子数目显著增加；在低于单载波微放电阈值的低功率持续时间电子会被吸收，电子数目减少。在多载波合成信号的作用下，电子数目会呈现多种演化方式，并不一定如单载波情况时电子数会随时间在对数坐标下线性变化。基于以上分析，单纯采用电子演化趋势来判断微放电的发生不再适用于多载波微放电的判断。为了进一步明晰多载波信号条件下微放电演化过程中电子数目、信号反射和传输、转化功率等特性，本节对典型同相相位分布的不同频率间隔、不同载波数的多载波信号进行微放电粒子模拟，以揭示多载波微放电的物理过程。

本节将利用粒子模拟工具，依据以上讨论所得的基于二次电子累积特性的多个包络周期和基于反射系数变化的单个包络周期微放电阈值判断依据，针对同轴传输线在不同频率间隔和不同载波数同相相位分布多载波信号作用下进行微放电粒子模拟，并对模拟结果进行对比和讨论，同时对不同配置参数条件下多载波微放电的微放电类型进行分析。

1.不同频率间隔条件下的多载波微放电粒子模拟［18］

中心频率为340 MHz、频率间隔为1.25 MHz、单路载波功率为15 W的同相相位分布6载波合成信号波形用浅灰色示于图4－6（a），其包络周期为800 ns。按照1 W的功率调谐步长，针对单路载波功率分别为12 W、13 W、14 W和15 W的多载波信号进行了粒子模拟，模拟时长1 600 ns。为了能够模拟激发微放电的最差情况，初始电子在t＝320 ns时刻加载。

从图4－6（a）可以看出，当功率从12 W增加至15 W时，峰值宏粒子数量从4.6×105（对应12 W）增加至3.0×106（对应15 W）。图4－6（b）、（c）分别给出了不同载波功率情况下，有、无初始电子的归一化反射波电压及其差值、电磁波向粒子的能量转化功率，相关数值示于表4－1。从表4－1可见，当单路载波功率从12 W增加到15 W，有、无初始电子的归一化反射波电压的最大变化量从0.75 dB显著增加到3.38 dB，转化功率从2.195 2 W显著增加到17.040 5 W。根据反射波电压增量1～3 dB的判断依据，则模拟所得的微放电阈值应介于12～15 W。同时，从图4－6（a）所示连续两个多载波合成信号包络周期的粒子累积趋势可以看出，第一个多载波包络周期中高功率包络期间累积的二次电子在下一个多载波包络周期中高功率包络到来之前就已完全湮灭，无法形成包络周期间的剩余电子累积，因而不足以激发多个包络周期微放电。

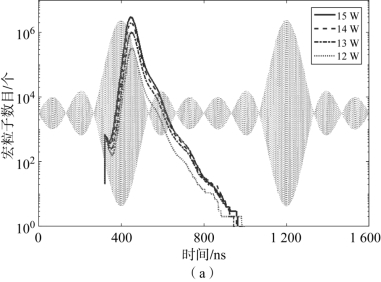
图4－6　频率间隔为1.25 MHz时不同载波功率的多载波微放电演化过程的粒子模拟（见彩插）

（a）宏粒子数量，浅灰色背景为供参照的同相多载波信号；

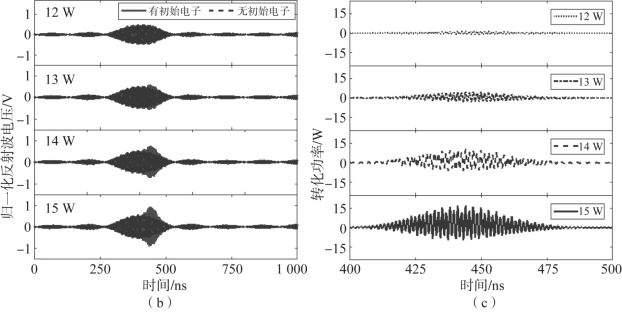
图4－6　频率间隔为1.25 MHz时不同载波功率的多载波微放电演化过程的粒子模拟（续）（见彩插）

（b）有、无初始电子的归一化反射波电压；（c）能量转化功率

表4－1　频率间隔为1.25 MHz时多载波微放电的模拟数据

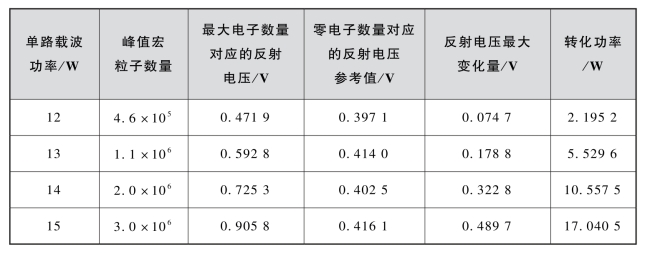
图4－7给出了单路载波功率为15 W时微放电演化过程的粒子三维分布。其中，初始时刻的种子电子与图4－5（a）相同，在t＝400 ns时，电子浓度显著增加，并在t＝449 ns时电子数目达到了最大值；但在该包络周期结束时，电子数目显著减少，如图4－7（c）所示，并且在下一个包络周期的高功率时段来临之前电子完全消失，如图4－7（d）所示。结合图4－6中反射信号的变化可以看出，该配置的多载波信号激发了单个包络周期微放电。

图4－7　频率间隔为1.25 MHz的多载波微放电过程中电子的空间分布（见彩插）

（a）400 ns；（b）449 ns；（c）800 ns；（d）1 000 ns

以上模拟结果表明，对于所选样件，当输入单路载波功率介于12～15 W时，频率间隔为1.25 MHz的6路UHF多载波信号将优先激发单个包络周期微放电，而非多个包络周期微放电。

为了进一步厘清单个和多个包络周期微放电间的关系，本节对2.5 MHz、5 MHz和10 MHz三种频率间隔情况的同相相位分布多载波信号进行粒子模拟分析。(www.xing528.com)

图4－8给出了频率间隔为2.5 MHz，单路载波功率分别为25 W、26 W、27 W和28 W时宏粒子数量随时间的变化曲线。合成信号波形用浅灰色示于图4－8中，可以看出，电子数整体呈下降趋势，即不足以激发多个包络周期微放电。而当功率从25 W增加至27 W时，峰值宏粒子数量从5.3×105（对应25 W）增加至5.0×106（对应27 W）。不同载波功率情况下，峰值宏粒子数量，有、无初始电子情况下的归一化反射波电压及其差值，电磁波向粒子的能量转化功率相关特性数值示于表4－2。从表中可以看出，当单路载波功率从25 W增加到27 W，有、无初始电子情况下的归一化反射波电压的最大变化量从1.41 dB显著增加到5.61 dB，转化功率从2.463 7 W显著增加到38.245 6 W。根据反射波电压增量1～3 dB的判断依据，模拟所得的微放电阈值应介于25～27 W。通过以上分析可以看出，对于2.5 MHz的频率间隔，单个包络周期微放电仍然被优先激发。

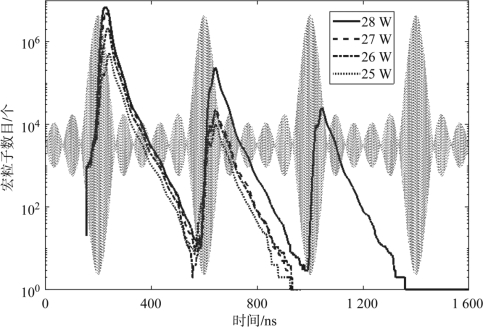
图4－8　频率间隔为2.5 MHz时宏粒子数量随时间和功率的变化（见彩插）

表4－2　频率间隔为2.5 MHz时多载波微放电的模拟数据

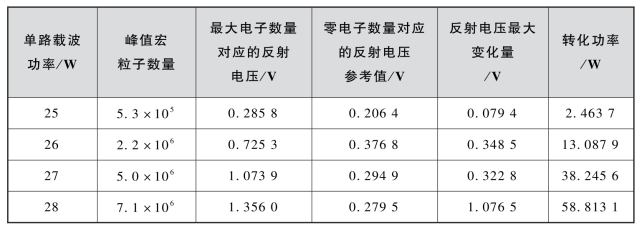
图4－9给出了频率间隔为5 MHz，单路载波功率分别为29 W和30 W时宏粒子数量随时间的变化曲线。合成信号波形用浅灰色示于图4－9中，可以看出，发生了多个包络周期微放电，阈值介于29～30 W。而在第一个包络周期内峰值宏粒子数量从1.1×105（对应29 W）增加到2.2×105（对应30 W），有、无初始电子情况下归一化反射波电压的最大变化量从0.16 dB增加到0.63 d B，小于1 dB的判断阈值。通过以上分析可以看出，对于5 MHz的频率间隔，多个包络周期微放电被优先激发。

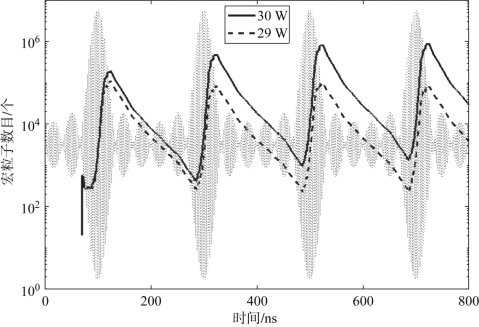
图4－9　频率间隔为5 MHz时宏粒子数量随时间和功率的变化（见彩插）

图4－10给出了频率间隔为10 MHz，单路载波功率分别为30 W和31 W时宏粒子数量随时间的变化曲线。合成信号波形用浅灰色示于图4－10中，可以看出，发生了多个包络周期微放电，阈值介于30～31 W。而在第一个包络周期内峰值宏粒子数量不足105，并且有、无初始电子情况下的归一化反射波电压的最大变化量不足1 dB，不足以激发单个包络周期微放电。通过以上分析可以看出，对于10 MHz的频率间隔，多个包络周期微放电同样被优先激发。

图4－10　频率间隔为10 MHz时宏粒子数量随时间和功率的变化（见彩插）

对比图4－6（a）、图4－8、图4－9和图4－10可以看出，随着频率间隔的增加，多载波合成信号的包络周期成比例减小，1.25 MHz频率间隔的包络周期为800 ns，而10 MHz频率间隔的包络周期为100 ns，前者是后者的8倍。结合粒子模拟结果可以看出，对于同相相位分布的多载波信号，当频率间隔较窄时，单个包络周期微放电被优先激发；当频率间隔增大时，包络周期变小，单个包络周期内难于激发微放电，剩余电子更容易在连续的多个包络周期间累积，从而激发多个包络周期微放电。

基于以上分析，发生多载波微放电的形式取决于多载波信号的载波频率间隔（或带宽），因而多个包络周期微放电并非一定被优先激发。对于多载波微放电“最坏状态”及全局阈值分析，应当同时考虑单个和多个包络周期两种形式的多载波微放电，并取两者中阈值更低者［18］。

2.不同载波数条件下的多载波微放电粒子模拟［19］

本节采用粒子模拟方法对3路、4路、5路和6路四种载波配置的10 MHz频率间隔多载波信号在连续包络周期间的二次电子瞬时波动情况进行数值模拟。

图4－11给出了四种不同载波配置的仿真结果。对于每一种载波配置，通过调整输入功率，能够观察到二次电子随时间增长和减少的涨落。由多个包络周期微放电判断依据，使电子数目涨落处于临界状态的每路载波的功率为给定载波配置的LMD阈值。对于任何给定的单个包络周期，没有足够的电子去激发单包络周期微放电。从图中可以看出，对于10 MHz频率间隔的所选四种载波数配置，在同轴传输线中观察到了多个包络周期微放电，LMD优先于SMD被激发。3路、4路、5路和6路四种载波配置的多载波微放电阈值分别为每载波95.2 W、62.7 W、38.7 W、30.4 W。随着载波数从3增加至6，每路载波阈值功率从95.2 W降低至30.4 W。同时，平均功率（载波数与每路载波阈值功率之积）变化趋势相同，从3载波的285.66 W降低到6载波的182.52 W。

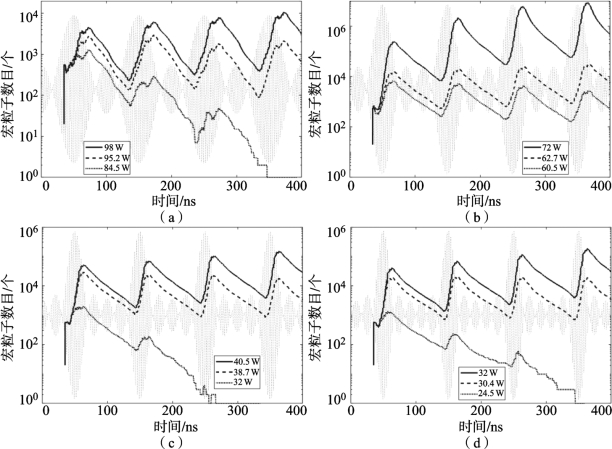
图4－11　频率间隔为10 MHz时不同载波数的多载波微放电宏粒子变化曲线

（a）3载波；（b）4载波；（c）5载波；（d）6载波