微放电演化过程粒子模拟-空间微波部件多载波微放电分析

随着计算机模拟技术的发展，基于器件级“第一性原理”的粒子模拟技术在真空电子器件研究中得到了广泛应用［1］。在微放电研究中，通过在离散网格上对麦克斯韦方程组和牛顿－洛伦兹方程进行迭代求解，模拟电场与粒子之间的相互作用，同时引入二次电子发射模型，描述电子与部件表面的碰撞过程，可以获得部件内部二次电子数量随时间的动态变化信息［2－9］。为了与第6章的多载波微放电实验研究相兼容，并期望获得稳定、可重复的多载波微放电测试数据，待分析样件选取了由两个标准TNC接头、两段阻抗变换段和一段142 mm长的标准同轴传输线组成的简单部件，如图4－1所示。同轴传输线的内外导体半径分别为5.77 mm和13.27 mm，保证其特性阻抗为50Ω，部件基材为铝合金，表面采用镀银处理，同轴传输线与TNC接头之间采用渐变阻抗变换段和内外径之间采用聚四氟乙烯支撑的同轴结构进行连接。

图4－1　同轴传输线实物

如第2章所述，多载波微放电存在多个包络周期微放电和单个包络周期微放电两种类型。根据图2－4，对于多个包络周期微放电，其阈值可以通过功率扫描，寻找包络周期间二次电子累积趋势接近平坦状态的临界功率，该功率即可视为多个包络周期微放电的阈值。如多载波信号功率超过此临界功率，无论二次电子累积的上升趋势如何缓慢，足够长时间后仍然会导致微放电的发生。但对于单个包络周期微放电，却难以通过这种趋势的判断得到相应的阈值。国际上的主流方法是采用电子渡越时间T20规则进行单个包络周期微放电阈值的判断，但利用该规则得到的单个包络周期微放电阈值并不能与基于二次电子累积特性得到的多个包络周期微放电阈值进行比较。为了能够进行两种阈值的比较，两种阈值的判断依据必须基于相同标准。对于基于粒子模拟的阈值对比而言，单个包络周期微放电阈值的判断标准应当同样基于二次电子的累积特征。只有这样，所得的单个包络周期微放电阈值才能和采用同一微波部件模型和二次电子发射模型得到的多个包络周期微放电阈值进行合理的对比。

需要注意的是，多载波微放电测试系统并不能区分所检测到的微放电的形式［10］。这就意味着对于测试系统而言，触发微放电的标准对于单个和多个包络周期微放电是相同的。这一共同标准就是测试系统的探测灵敏度。对于特定的测试系统，其探测灵敏度是给定的。微放电测试的基本原理是测量待测部件的传输特性（即散射参数S11和S21）的变化［10］。真空腔体内充斥二次电子的空间可以视为广义的等离子体，其等效介电常数与二次电子密度（或总量）正相关［11］。在大功率微波激励电场的作用下，电子数量会迅速增加。当二次电子总量达到一定程度，使部件的传输特性发生的变化可以被测试系统以其灵敏度探测得到时，此时的入射信号功率即为“测试阈值”。这与实验测量中采用正反向调零来检测反射信号的变化从而判断是否发生微放电是一致的。

尽管测试系统可以得到微放电阈值，由于微放电发生过程是在瞬时（纳秒量级）完成的，目前我们还不能通过测试系统获取微放电阈值与二次电子累积总量之间的关系。但是，这一关系可以通过粒子模拟得到。在粒子模拟过程中，电子数随时间变化及其引起的部件反射系数（S11）变化是可以同时得到的。对于未加载初始电子的待测部件，测量所得的S11参数反映的是由于部件自身的阻抗特性引起的反射波与入射波幅度之比。加载初始电子后并发生二次电子倍增，电子数量的增加会导致阻抗不匹配，引起反射波的增加，相应地改变S11参数［12］。与实际反射测量系统存在对于反射系数变化的最小分辨率和最短响应时间相比，粒子模拟方法对于反射系数变化分析的分辨率和响应时间仅受有效数字位数和所用时间步长的限制。因此，通过粒子模拟可以得到无法通过实验系统得到的电子数量与反射波幅度之间的关联，进而得到基于电子累积数量的单个包络周期微放电阈值判断依据。

为了得到上述微放电判断依据，首先采用单载波激励信号对图4－1所示部件进行了微放电演化过程的模拟。模拟中采用了商业粒子模拟软件CST Par⁃ticle Studio［13］，采用银的修正Vaughan SEY模型［14］和包含1 000个电子的宏粒子。单载波频率设置为340 MHz，归一化入射波电压为26 V，高于其模拟获得的单载波微放电阈值20 V。

对于所采用的同轴结构，电磁场沿－z方向传播，端口1和端口2分别设为微波信号的输入端和输出端，其端口特性阻抗为50Ω。为了保证模拟结果的准确性，需要在各个方向上进行合理的网格剖分，在x、y、z三个方向上的网格数分别为55、55和111，同时保证在内外径之间有10个网格，这样可以有效保证数值模拟的精度。进行迭代的时间步长为0.75 ps，模拟总时长为400 ns。作为基准，首先在无初始电子条件下进行模拟，所得归一化反射电压为0.38 V，对应的S11为－36.70 dB。图4－2给出了粒子模拟所得的宏粒子数量，有、无初始电子情况下归一化反射波电压以及电磁波向粒子能量转化功率随时间的变化曲线。

由图4－2（a）可以看出，在70 ns以内，电子数量在对数坐标下呈线性增长，但在该时间段内反射信号幅度与无初始电子的情况几乎相同，如图4－2（b）所示。表明此时二次电子数量虽按指数增长，但其总数仍不足以引起可觉察的反射系数变化，称此阶段为微放电的“建立区”。当模拟时间大于300 ns时，宏粒子数量趋于3.6×106个，如图4－2（a）所示，这是由于空间电荷效应导致的电子之间相互排斥，使得宏粒子数目达到临界状态后趋于饱和［15－17］。对比图4－2（b）可以看出，该时间段内归一化反射波电压趋于稳定，达到0.9 V，对应的S11为－29.21 dB，称此阶段为微放电的“饱和区”。

图4－2　单载波微放电演化过程的粒子模拟［18］（见彩插）

（a）宏粒子数量；（b）归一化反射波电压；（c）转化功率

模拟时间介于70～300 ns时，从图4－2（a）可以看出，宏粒子数量不再随时间呈指数增长，对应的由电子累积导致的归一化反射波电压从0.38 V显著变化到0.9 V，如图4－2（b）所示。该时间区段可视为微放电的“临界区”。根据前述微放电测试时基于反射波变化的检测原理，在此区间内测量得到的阈值均可合理地视为“测试阈值”。对于给定的实验系统，其测量所得到的“测试阈值”及其对应的微放电发生的时刻则由该实验系统对于反射波幅度变化的探测灵敏度确定。因此，上述“临界区”的定义合理地解释了不同微放电测试系统得到的“测试阈值”有所不同的内在原因。(www.xing528.com)

我们以“建立区”中的反射系数为参考值，以“临界区”中反射系数相对参考值增加1～3 dB作为界定临界单个包络周期微放电的判断依据。对于现代微波测试系统而言，1～3 dB的反射系数变化已显著大于S11测量中由于噪声及时域抖动引起的测量值波动（通常低于1 dB），因此采用这一判断依据所得的微放电阈值范围是合理的，并且所得结果可以与实验结果相比较。

以待分析样件为例，当反射系数增加3 dB时，反射信号的归一化电压为0.54 V，对应图4－2（a）中“临界区”的时刻为133 ns，此时宏粒子数量约为106个。图4－2（c）给出了上述过程中电磁波向粒子能量转化的功率曲线。由图可见，在微放电“建立区”，转化功率极小；在微放电“临界区”，转化功率显著增加；在微放电“饱和区”，转化功率趋于稳定。上述变化趋势与归一化反射波电压的变化规律一致。

图4－3给出在400 ns附近时同轴传输线归一化入射波和传输波电压。从图中可以看出，两者除了幅值有微小差别外（相差0.15 V），传输波几乎与经过延时的入射波完全相同。由此可知，微放电对传输波的幅度影响微小，但在400 ns时反射波电压已经发生了显著变化，这也是实验中通常采用监测反射系数来测量微放电的原因。

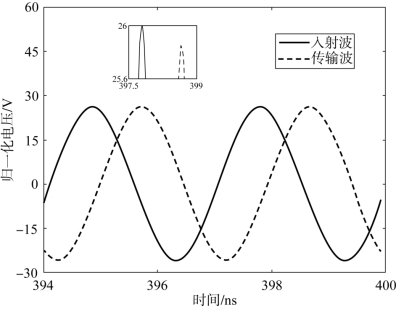
图4－3　归一化入射波和传输波电压

图4－4给出了在输出端口处监测的传输波频谱分布。从图中可以看出，由于微放电达到了饱和状态，大量二次电子导致了非线性，产生了传输波的二次谐波分量和三次谐波分量，其中二次谐波的幅度比传输波幅度小约65 dB，因此，实际微放电测试系统中也通常采用谐波法来进行微放电检测。

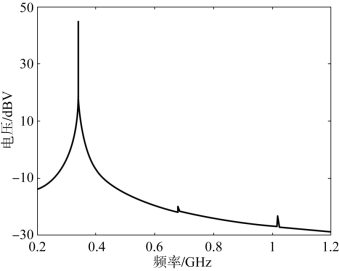
图4－4　微放电演化过程中传输波频谱变化

图4－5分别给出了t＝1 ns、70 ns、133 ns和300 ns时粒子的三维分布。在t＝1 ns时，在同轴传输线中间处内径的表面采用均匀发射的方式加载种子电子，随着时间的推移，电子数逐渐增多。在t＝70 ns时，电子主要集中在中间区域，由于电子的扩散特性，当达到饱和状态后电子充满同轴传输线内外径之间的整个空间。

图4－5　微放电过程中电子的空间分布（见彩插）

（a）1 ns；（b）70 ns；（c）133 ns；（d）300 ns