多载波微放电统计理论介绍

近年来，在多个包络周期多载波微放电研究中，Anza等［5］通过采用非稳态模型的微放电统计理论，考虑了单表面和双表面二次电子碰撞特性，将时间分析窗口扩展到多个多载波包络周期，从而实现对二次电子数目的动态建模，提出了一种适用于平行平板结构的多载波条件下二次电子累积的理论分析方法，该方法同时适用于稳态和非稳态两种情形。

任意多载波信号可表示为式（2－1），对于等频率间隔分布的多载波信号，其包络是周期的，周期Te＝1／Δf。与单载波微放电统计理论不同的是，这里对电子进行加速的电场由多个频率的电场叠加而成，为了推导方便将多载波信号平移－π／2，可得电场：

式中，Ei为单路载波对应的电场幅度；ωi＝2πfi为每路载波的角频率。根据洛伦兹方程获得多载波信号激励条件下电子运动的轨迹方程：

式中，m和－e分别为电子的质量和电量。

通过推导并进行归一化处理，可以获得出射速率与电子渡越时间、初始相位及位移的关系。为了方便表示，引入参数E、Ω、Φ分别表征多载波信号的电场幅度、频率和相位信息：

式中，

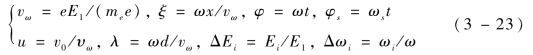(www.xing528.com)

在3.3节非稳态微放电统计理论的基础上，采用变量概率的转移法则，以电子出射速率的概率分布函数构造电子渡越时间、初始相位和位移的联合概率密度函数G（τ｜φs；ξ，E，Ω，Φ）：

式中，为函数进行单调化处理后的函数。同样考虑上下两极板的四种碰撞方式，以下极板为参考，上极板的电场方向相反，因此四种概率密度函数分别为：

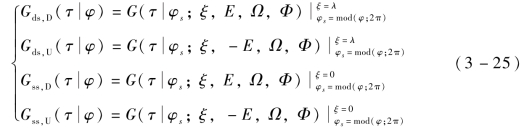
式中，下标ds和ss分别表示双边和单边碰撞；下标U和D分别表示上极板和下极板；注意到联合概率密度函数中定义适用于任意多载波信号。

有了以上四种概率密度函数，多载波条件下的电子数目可采用式（3－15）～式（3－19）计算获得。基于多载波微放电统计理论，对平行平板结构在C频段同相相位分布6载波信号作用下进行了微放电仿真和计算。平行平板的间距为0.43 mm，假设平行平板表面镀银，采用ECSS给定的银的SEY参数，6路载波信号的频率分别为3.57 GHz、3.67 GHz、3.77 GHz、3.87 GHz、3.97 GHz和4.07 GHz，频率间隔为100 MHz，包络周期为10 ns，每路载波具有相同的电场强度E0。图3－5给出了V0＝E0 d＝30 V和V0＝20 V时计算获得的电子数目随时间的变化过程。所选的两种电压分别使得电子数目随时间总体上升和下降。从图中可以看出，基于统计理论的计算结果与数值模拟结果吻合良好。

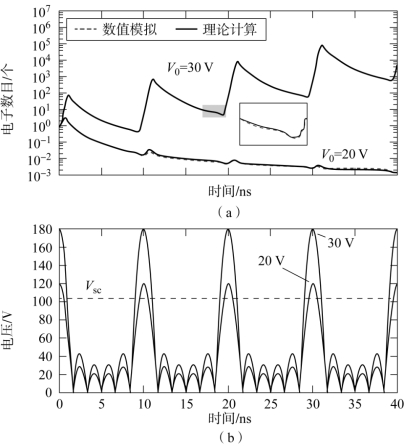
图3－5　基于统计理论计算的平行平板多载波微放电电子数随时间变化过程［5］

该方法是通过求解均匀场分布条件下的一维运动方程，因此只能适用于平行平板结构。同时，该方法每次都需要对概率密度函数进行重新计算，特定相位组合多载波信号的微放电计算耗时在小时级。