为了克服稳态模型无法计算二次电子动态演化过程的缺点，Anza等［2］提出了适用于单载波的非稳态微放电统计理论，该理论不仅能够预测单载波微放电阈值，还能够模拟信号功率高于微放电阈值时的电子数增长过程以及低于微放电阈值时的电子数降低过程，同时考虑了单边和双边碰撞。不同于Vdov⁃icheva等［1］提出的需要稳态假设的统计理论，该理论同时适用于稳态和非稳态情形，为微放电演化过程的理论分析提供了普适和可信的理论工具。
为了有效表示单边碰撞和双边碰撞，将平行平板的上下两个极板分别记为“U”和“D”，则平行平板结构中的碰撞分为单边碰撞（U－U和D－D）和双边碰撞（U－D和D－U）两种，如图3－1所示［2］，其中ss代表单表面碰撞，ds代表双表面碰撞。由于从不同极板出射的电子方向相反，因此统一采用下极板作为位移和相位的参考进行分析。
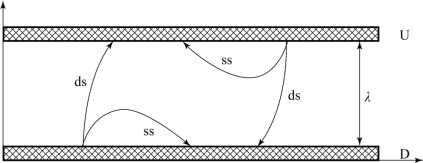
图3－1 平行平板结构中单边和双边两种碰撞类型示意图［2］
根据碰撞方式的不同，以稳态模型中的联合概率密度函数
构造四种不同的概率密度函数：
式中，ds表示双边碰撞，对应的归一化位移为λ；ss表示单边碰撞，对应的归一化位移为0；标号U或者D表示电子从上极板或下极板出发的运动情况。考虑到从上极板出发时，电场需要反向，因此，上极板和下极板的相位相差π。
通过考虑上下两个极板电子的出射速率和碰撞速率，从而获得总电子数目随时间的变化过程。这里，首先考虑上极板电子的出射速率CU（φ），对于特定的相位φ，碰撞电子的数目由两部分构成：从下极板出射经过双边碰撞的电子和从上极板出射经过单边碰撞的电子，因此
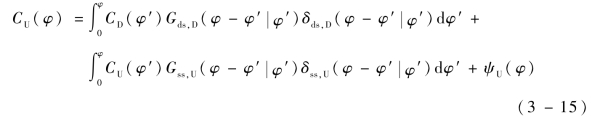
式中，ψU（φ）表示外部电子源引入的二次电子。
相应地，下极板电子的出射速率CD（φ）由两部分构成：从下极板出射经过单边碰撞的电子和从上极板出射经过双边碰撞的电子，因此
式（3－15）与式（3－16）在数学上组成Volterra积分方程组。同时，考虑到电子在上下两个极板碰撞也会导致二次电子数目减少，在特定相位φ时上极板的电子碰撞速率也由两部分构成：从下极板出射经过双边碰撞的电子和从上极板出射经过单边碰撞的电子，因此
(www.xing528.com)
相应地，下极板的电子碰撞速率也由两部分构成：从下极板出射经过单边碰撞的电子和从上极板出射经过双边碰撞的电子，因此
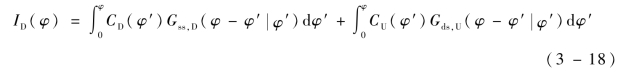
综合考虑电子的出射速率和碰撞速率，在相位φ时刻，两平行平板之间的总电子数应等于上、下极板处的出射速率减去碰撞速率，并对时间进行积分获得总电子数目随时间的变化过程：
图3－2给出了基于稳态和非稳态统计理论计算的平行平板结构微放电敏感曲线［2］。与传统的基于常数k和常数v的微放电敏感曲线相比，基于统计模型的敏感曲线与数值模拟结果和实验结果在下边界处更为吻合。同时，相对于稳态模型，非稳态模型还考虑了单边碰撞的情况，因此，基于非稳态统计理论的敏感曲线与数值模拟结果更为吻合。林舒等［3］将非稳态统计理论推广至电场非均匀分布的同轴传输线结构，同时针对传统稳态模型只能考虑双边碰撞的缺点，提出了一种能够考虑所有碰撞的改进稳态模型，并计算了平行平板结构的微放电敏感曲线，如图3－3所示［4］。从图中可以看出，由于改进稳态模型和非稳态模型都考虑了微放电过程中的所有碰撞类型，所以基于两者计算的微放电敏感曲线基本一致。但由于非稳态模型在微放电达到稳态前需要计算相当长周期的微放电动态演化过程，相对于稳态模型更为耗时。而改进稳态模型和稳态模型的计算时间几乎相同，所以改进稳态模型在计算微放电敏感曲线时在保证计算精度的条件下耗时更少。
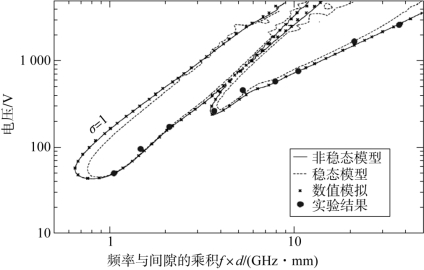
图3－2 基于统计理论的微放电敏感曲线与数值模拟及实验结果的比对［2］
图3－3 基于改进稳态模型的微放电敏感曲线［4］（见彩插）
图3－4给出了基于非稳态统计理论计算的频率为1.64 GHz、间距为1 mm的平行平板在电压V0＝120 V和V0＝10 V时电子数目以及出射速率和碰撞速率随时间的变化曲线，并与数值模拟结果进行了比较［2］。由于考虑了电压高于微放电阈值时的电子数增长过程以及低于微放电阈值时的电子数降低过程，使得基于非稳态统计理论计算的电子数目波动曲线与数值模拟结果吻合良好。
图3－4 基于非稳态统计理论计算的频率为1.64 GHz、间距为1 mm的平行平板电子数目以及出射速率和碰撞速率随时间的变化与数值模拟结果的比较［2］
（a）V0＝120 V；（b）V0＝10 V
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
