2.4　电子渡越时间T20规则

电子渡越时间T20规则的原始表述如下［7］：

“As long as the duration of the multicarrier peak and the mode order of the gap are such that no more than twenty gap－crossings can occur during the multicarrier peak，then multipaction－generated noise should remain well below thermal noise（in a 30 MHz band）.”

该规则意味着只有当多载波波形的包络高于单载波微放电阈值的持续时间使得电子能够在平行平板两极板间渡越超过20次才发生微放电。也就是说，T20规则允许多载波信号的包络在短时间内处于单载波微放电阈值之上，只要电子渡越的次数不超过20即可。相对而言，N2 P规则即为0个电子渡越时间，也就是说，它不允许多载波信号的包络以任意短的时间处于单载波微放电阈值之上，不允许任何的电子倍增。相对于N2 P规则，T20规则为多载波微放电提供了一个放宽的设计依据。在微波部件设计时，如果单载波微放电阈值在最大可能峰值功率之上，则选择N2 P规则及对应的余量，否则采用T20规则［6］。

电子渡越时间T20规则是在对多载波微放电模拟和试验结果进行分析的基础上得出来的，然而在微放电试验中发现，当电平持续超过阈值99个电子渡越时间时，在信号输出端才能检测到高于－70 d Bm噪声电平的附加电平［13］。在微放电中电子数目随着电子渡越时间指数增长，20个电子渡越时间和99个电子渡越时间形成的电子数目差异巨大，因此20个电子渡越时间规则偏保守。但是T20规则是研究人员试图放宽多载波微放电发生条件的重要尝试，并在ESA的微放电设计及测试标准中作为建议指导各宇航机构进行微波部件多载波微放电设计及验证。

电子渡越时间T20规则只是给出了发生微放电的条件假设，并未给出实际设计中单载波等效功率的计算方法。因此，在进行微波部件设计时，需结合多载波频率、功率以及微波部件的关键区域间隙来确定满足电子渡越时间T20规则的等效功率P20，其定义为［6］：多载波波形达到单载波微放电阈值的时间宽度使得电子在微放电区域渡越20次的峰值功率（“peak power of the multicarrier waveform whose width at the single carrier multipaction threshold is equal to the time taken for the electrons to cross the multipacting region 20 times”）。其中20次电子渡越时间T20＝10*n／fmean，其中，微放电阶数n可根据频率和微放电关键区域的间隙尺寸查表获得［6］，fmean为多载波信号的平均频率。

对于等频率间隔、等幅度分布的多载波信号，边界函数法是获得P20等效功率最有效的方法，该方法由Wolk等［14］于2000年提出。边界函数法通过对T20时间内的多载波信号能量进行放大，取其上界，获得的等效功率为：

式中，A0为每路载波的幅度；N为载波数；Δf为载波间的频率间隔。该边界函数只适用于载波频率间隔相等、载波幅度相同的情况，同时该函数为经验公式，缺乏明确的物理意义，在微放电阶数较低时，得到的等效功率超过了最大可能峰值功率N2 P，与信号处理的基本理论不符［13］；针对这一问题，Udiljak等［13］提出了修正的边界函数，并将其扩展到载波幅度不等的情形，等效功率可表示为：

Angevain等［15］对给定时间内多载波信号的平均功率表达式进行推导，并进行不等式放大，获得了边界函数：

式中，Ai和fi分别为每路载波的幅度和频率，i＝1，2，…，N。

对于初始频率为12 GHz、频率间隔为0.04 GHz的10载波信号，每路载波的幅度为10 V，采用Wolk和Udiljak提出的边界函数进行等效功率分析，随着不同T20时间其等效单载波功率如图2－5所示。从图中可以看出，随着T20的增加等效功率变小，同时Udiljak所提的边界函数在T20较小时，采用最大峰值功率进行替代，有效避免了Wolk所提边界函数的缺点。但是这两种边界函数只适用于等频率间隔的情况。同时需要说明的是，在本节中电压对阻抗进行了归一化。

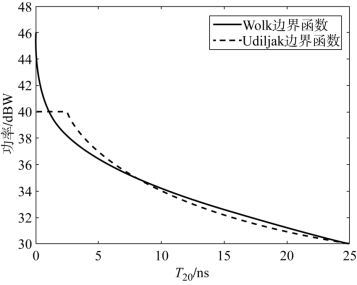
图2－5　Wolk和Udiljak所提出边界函数的比较

获取P20等效功率的实质是将多载波信号的高功率部分尽量挤压进T20时间内，因此另一种更为直接的获得等效功率的方法是采用优化工具进行T20时间内信号的直接优化。其中一种是采用Matlab的非线性最小方差（Non－Linear Least Square，NLSQ）函数来获得使T20时间内能量最大的相位分布；还有一种产生大量的随机相位分布和对应的包络分布，然后进行比较和相位修正，从而获得最大等效功率。在频率非均匀分布时，后一种方法比非线性最小方差法具有优势，因为非线性最小方差法需要较好的种子相位分布从而获得局部最小值；但当载波数目巨大时，后一种方法进行计算需进行大量相位分布的比较及修正才能获得较好结果［16］。为了获得好的优化效果，可以把这两种方法结合起来，采用后一种方法所获得的结果作为非线性最小方差法的种子相位分布，从而获得全局最大的等效功率。

采用遗传算法可以大大减少计算量，特别是对频率间隔非均匀分布的情形。采用遗传算法的优点在于不仅能找到非线性最小方差法找到的局部极大值点，还能找出全局极大值点。Merecki等［17］把遗传算法加到了WCAT（Worst Case Assessment Tool）软件中，并对其中的优化部分进行了修正。

本节介绍一种基于修正差分进化算法确定周期内多载波微放电等效功率的全局优化方法［18］。该方法针对单个包络周期微放电等效功率的全局优化问题，推导获得了T20时间内信号能量的表达式，采用二次插值法进行局部搜索，采用修正差分进化算法进行全局优化，确保获得全局最大值，从而确定单个包络周期微放电等效功率。所提出方法不仅能够适用于幅度不同、频率间隔不等的多载波信号情况，并且能够提供微放电“最坏状态”相位分布，为多载波微放电实验验证提供相位输入。

多载波合成信号的复数形式可表示为：

式中，N为载波数；Ai为载波幅度；fi为载波频率；φi为载波初始相位，i＝1，2，…，N。多载波信号的瞬时功率为：

可以看出，其瞬时功率与各路载波信号的幅度、频率和初始相位相关，以t0为中心，时间τ内的信号能量为：(www.xing528.com)

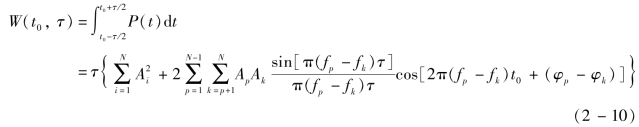
根据电子渡越时间T20规则，为了获得最大等效功率，多载波信号的高功率持续时间应尽量集中于T20时间内，需要获得T20时间内信号能量的最大值。而T20与微放电阶数、载波平均频率以及关键区域间隙尺寸相关联，对于特定结构微波部件和特定工作频率的多载波信号其T20可查询获得［6］。对于给定的卫星通信参数，其多载波信号的幅度和频率是预先确定的，观察信号能量的表达式可以看出，不同的初始相位分布使得该信号在［t0－T20／2，t0＋T20／2］时间段内能量不同。而电子渡越时间T20规则下的多载波微放电“最坏状态”就是该能量最大时对应的初始相位组合，因此采用全局优化算法搜索满足条件的全局最优解是确定多载波微放电“最坏状态”的关键。

差分进化算法是基于群体智能理论的优化算法，通过群体内个体间的合作与竞争产生新的群体从而指导优化搜索［19］。它保留了基于种群的全局搜索策略，采用实数编码、基于差分的变异操作和一对一的竞争生存策略，降低了遗传操作的复杂性，同时它特有的记忆能力使其可以动态跟踪当前的搜索情况以调整其搜索策略，具有全局收敛能力。

多载波合成信号的幅度随时间变化剧烈，局部极值点数量巨大，为了获得T20时间内信号能量最大的相位组合，不仅要对局部最优解进行快速搜索，同时要确保其收敛到全局最优解。而传统的差分进化算法过于注重跳出局部最优解，虽然可以确保获得全局最优解，但是在进行局部搜索时，其搜索效率低下。针对多载波合成信号T20时间内信号能量优化问题的特点，本节采用修正的差分进化算法来有效解决“最坏状态”搜索的问题［20］，其算法主要步骤如下：

（1）设置种群规模NP，最大进化代数Gen、缩放因子F和交叉概率CR。

（2）初始化种群，并通过优化函数公式f（φ1，φ2，…，φN）＝－WT20（φ1，φ2，…，φN）计算每个个体的函数值。

（3）对NP种群进行差分进化算法的变异、交叉、选择操作。

（4）采用二次插值法进行局部搜索，产生满足条件的个体进行替换，其分步骤如下：

（4.1）找到步骤（3）处理后的种群中函数值最大的个体l、函数值最小的个体h，它们对应的函数值分别为f（l）和f（h）；

（4.2）设置x1＝l，再从步骤（3）处理后种群中随机选取两个体x2，x3，且满足x2，x3≠l。采用式（2－11）得到新个体p＝（p1，p2，…，pN）：

式中，i＝1，2，…，N；xj＝（xj1，xj2，…，xjN）；j＝1，2，3。

（4.3）如果新个体p中任一pi不在［0，2π）之内，则越界，转向步骤（4.2）；否则根据优化函数公式f（φ1，φ2，…，φN）＝－WT20（φ1，φ2，…，φN）计算p的函数值f（p），如果f（p）≥f（h）转向步骤（4.2）；

（4.4）如果f（p）＜f（h），则用p代替当前最小函数值对应的个体h，即h＝p，结束步骤（4）。

（5）判断：若满足优化条件，则停止，输出优化结果；否则转向步骤（3）。

其优化流程图如图2－6所示。采用本方法可以快速实现T20时间内信号能量的最大值求解，确定电子渡越时间T20规则下微放电“最坏状态”及等效功率。同样，对上述频率和幅度配置的10载波信号进行分析，对T20时间内的信号能量采用修正的差分进化算法进行优化，假设待分析微波部件的间隙为1 mm，根据初始频率和间隙的乘积查询可知T20＝7.5 ns，其中（φ1，φ2，…，φN）为优化变量，0≤φi＜2π，i＝1，…，N，为了实现T20在单个包络周期内，t0∈［3.75，21.25］。

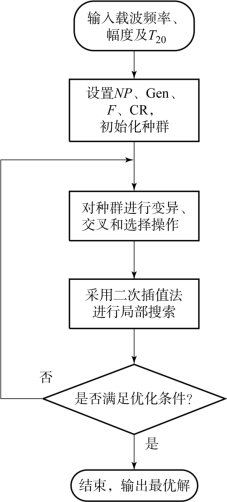
图2－6　基于差分进化算法进行T20时间内信号能量优化的流程图

当t0＝12.5 ns时，经优化可得初始相位（φ1，φ2，…，φN）为（207.98，22.92，194.81，0.11，154.70，300.80，95.68，261.27，72.77，248.09）时，T20时间内能量取全局最大值，对应的等效功率和等效电压分别为3 161.60 W和56.23 V，并且“最坏状态”时信号能量主要集中在T20以内。

另外，采用本方法可以对频率间隔不等或幅度分布不同的多载波信号进行处理，由于各个载波幅度初始相位的信息都包含在T20时间内信号的能量表达式中，只要对不同初始相位的信号能量进行优化，获得其最大值即可。本节对10路频率间隔相同、幅度不同的多载波信号进行分析，载波1到载波8的电压为10 V，载波9和载波10的电压为15 V，频率分布和上述例子相同。采用所提出方法进行优化可得，当初始相位（φ1，φ2，…，φN）为（157.56，341.48，167.88，0，204.55，63.60，274.45，110.01，297.94，122.61）时，T20时间内信号能量最大，对应的等效功率和等效电压分别为3 801.90 W和61.66 V。可以看出对于10路多载波信号，当其中两路载波幅度增大时，等效电压提高。

同时，采用本节提出的方法对幅度相同、频率间隔不同多载波信号进行了优化，载波1到载波8频率间隔为0.04 GHz，载波8和载波9以及载波9和载波10之间的频率间隔为0.08 GHz，载波幅度为10 V。采用所提出的方法进行优化，当初始相位（φ1，φ2，…，φN）为（243.51，55.58，221.73，17.76，167.30，327.16，140.37，329.45，66.46，83.65）时T20时间内能量最大，对应的等效功率和等效电压分别为2 826.53 W和53.17 V。可以看出对于10路多载波信号，当其中两路载波的频率间隔展宽时，等效电压下降。

本节介绍了电子渡越时间T20规则以及基于该规则获得等效设计功率的方法。重点针对单个包络周期微放电等效功率的全局优化问题，推导获得了多载波合成信号T20时间内能量的表达式，采用二次插值法进行局部搜索，采用修正差分进化算法进行全局优化，从而获得全局最优解，确定了单个包络周期微放电等效功率。所提出方法不仅能够适用于幅度不同、频率间隔不等的多载波信号情况，并且能够提供微放电“最坏状态”相位分布，为多载波微放电实验验证提供相位输入，所提出方法比传统的基于经验公式的方法具有明显优势，为空间宽带多载波工作微波部件微放电设计提供有效依据，对卫星转发器多载波微放电分析及设计具有一定价值。