多载波合成波形特性的分析介绍

多载波合成波形的幅度和频率是随时间变化的，依赖于每路载波的幅度、频率和相位分布。任意多载波波形V（t）可表示为［1，2］：

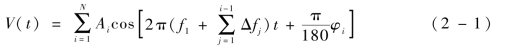
式中，N为载波数；Ai和φi为第i路载波幅度和初始相位；f1为第1路载波的频率；Δfj为第j路载波和第j＋1路载波的频率间隔。

为了方便，本节将N路载波信号的初始相位组合表示为Φi＝［φi1，φi2，…，φiN］。当给定所有Δfj，V（t）的包络是周期性的，周期为所有载波频率对应周期的最小公倍数［3］。

当幅度相同、频率间隔相等时，即Ai取A0，Δfj取Δf。在这种情况下，多载波合成波形V（t）只取决于初始相位φi，式（2－1）可简化为：

在同相相位分布时即所有载波相位φi取0时，式（2－2）可简化为：

可以看出，同相相位分布的多载波合成信号的最大瞬时幅度为NA0，为单路载波幅度的N倍，这种等频率间隔分布的多载波合成信号其包络周期为1／Δf。

对于“三角相位”分布的情况，即N个载波的初始相位为离散的线性关系，对于N为奇数和偶数波形不同，当N为偶数时，其合成波形可描述为：

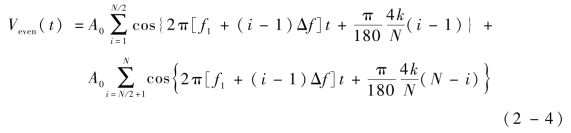
式中，k为100左右的常数。

图2－1给出了初始相位为同相相位分布φi＝［0，0，0，0，0，0，0，0］、三角相位分布φi＝［0，51.175，102.35，153.525，153.525，102.35，51.175，0］以及一种特定相位分布φi＝［0，75，150，300，300，150，75，0］的三种典型相位分布的8载波合成信号在单个包络周期内的时域波形。为了观察更为直观，同时和后面章节的仿真相对应，这里均对多载波合成波形在时间轴上平移了半个包络周期。(www.xing528.com)

观察图2－1给出的三种在一个包络周期内能量分布特性不同的多载波时域合成波形。对同相相位分布，连续低功率包络的持续时间比连续高功率的持续时间长很多；与之相反，三角相位分布多载波信号连续高功率包络在包络周期中占据主导。图2－1（c）所示的波形介于两者之间，在一个包络周期内没有占主导的连续高功率或连续低功率包络。从图中可以看出，对于相同的幅度A0、初始频率f1和频率间隔Δf，不同的初始相位φi会形成具有完全不同峰均比（Peak－to－Average Ratio，PAR）的波形，而每种波形对应不同的多载波微放电阈值。

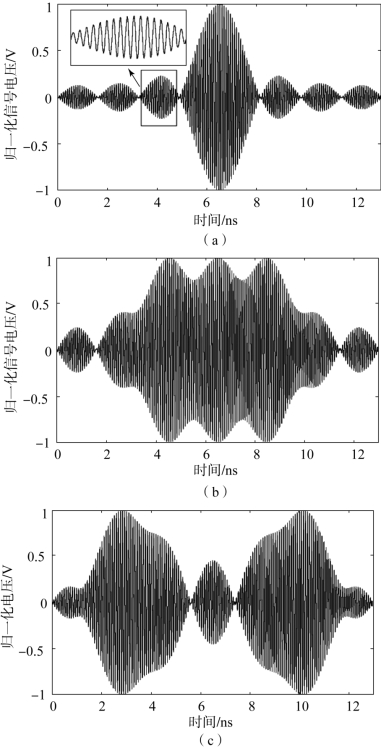
图2－1　初始频率为11.744 GHz，频率间隔为0.076 6 GHz的8载波信号一个包络周期内的时域波形［1，2］

（a）同相相位分布φi＝［0，0，0，0，0，0，0，0］；（b）三角相位分布φi＝［0，51.175，102.35，153.525，153.525，102.35，51.175，0］；（c）特定相位分布φi＝［0，75，150，300，300，150，75，0］

图2－2给出了中心频率为340 MHz、初始相位为同相相位分布的四种不同频率间隔的6载波时域合成波形，频率间隔分别为1.25 MHz、2.5 MHz、5 MHz和10 MHz。从图中可以看出，随着频率间隔的增加，多载波合成波形的包络周期成比例减小，1.25 MHz频率间隔的包络周期是10 MHz频率间隔的8倍。通过比较可以看出，相对于宽频率间隔，窄频率间隔的高功率持续时间显著增加。另外可以看出，频率间隔对多载波合成波形影响显著。

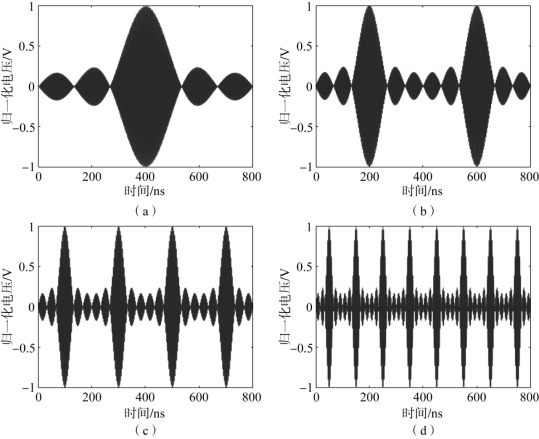
图2－2　频率间隔不同的6载波同相相位分布的多载波时域合成波形

（a）1.25 MHz；（b）2.5 MHz；（c）5 MHz；（d）10 MHz

图2－3给出了中心频率为340 MHz、频率间隔为1.25 MHz、初始相位为同相相位分布的四种不同载波数的多载波时域合成波形，载波数分别为3、4、5和6。从图中可以看出，对应于相同的频率间隔，其包络周期相同。在单个包络周期内零点的个数为载波数减去1，并且随着载波数的增加，合成包络的主瓣宽度逐渐减小，因此，载波数同样对多载波合成波形影响显著。

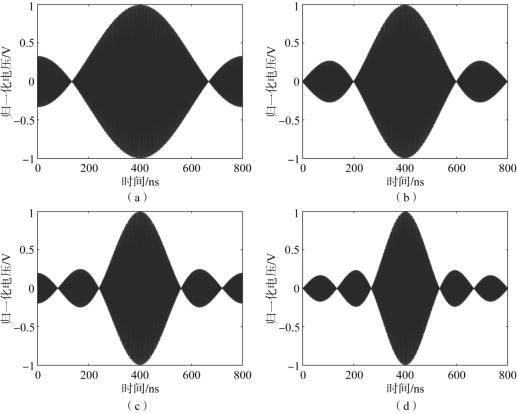
图2－3　载波数不同的1.25 MHz频率间隔同相相位分布的多载波时域合成波形

（a）3载波；（b）4载波；（c）5载波；（d）6载波

从以上分析可以看出，对于多载波合成波形而言，其受初始相位、载波频率间隔、载波数的影响显著。从本书第4章中粒子模拟的结果可以看出，连续高功率和连续低功率包络对微波部件中二次电子数目随时间变化影响显著。因此，要在考虑如此多影响因素、特别是初始相位的情况下进行多载波微放电分析是极具挑战性的。