附录　非线性/混沌/自组织

一、线性与非线性

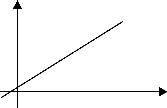
图4-1

【线性】

y=ax+b

两个变量之间具有正比例关系，在笛卡尔坐标平面上表示为一条直线。

【非线性】

y=ax2+bx+c

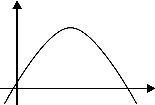
图4-2

两个变量之间没有正比例关系，在笛卡尔坐标平面上表示为一条曲线。

【非线性相互作用】

线性作用所揭示或包含的系统内部的关系是单向的、一次性的、静态的，其结果总是确定的。

图4-3

非线性相互作用所揭示或包含的系统内部的关系至少是双向的，循环反复和动态的，其结果往往是不确定的。非线性系统一般说来不可解，也不是叠加的。不能用数学式写出它的解。

【自然和社会存在大量非线性复杂现象】

[风洞实验室中的旗帜]

空气均匀地、简单地流动，均匀地、简单地撞击旗帜，但旗帜却飘忽不定，毫无规律。

[股票市场]

股票简单地从一个人转移给另一个人，但股市却暴涨暴跌，毫无规律。

[大脑功能]

每个神经元在简单地“刺激-反应”，但大脑却有若干不同的稳定的功能：正常人；癫痫；疯子（疯子还有各种类型的疯子）……

[天气]

空气温度、湿度、密度简单地变化，但天气发生突变。

[种群繁衍]

生物种群可以用递推式Xn+1=λXn（1-Xn）简单描述：第（n+1）代虫口数可从第n代虫口数简单推定得到，但种群却表现扩大或萎缩，毫无规律。

[贝纳德流]

每颗水分子在简单地受热、运动，但整体却显现小泡，每个对流泡或者左旋或者右旋，它们左旋、右旋相间。可是，在容器中的某处是右旋还是左旋？毫无规律。

【确定性和随机性】

（1）轨道、可预见、机械、线性、确定。

（2）统计概率可预见，宏观确定、微观不确定。

（3）不可预见、非线性、不确定、完全随机。

（4）既随机又确定：混沌：非周期确定。

二、混沌的发现

【周期三乱七八糟】

[李天岩的故事]

1973年4月一天。在美国马里兰大数学系，中国留学生李天岩问他的导师：“老板：有什么小题目做，来点容易做的。”约克想了想答：“试试区间迭代问题怎样？”

迭代：对于同一质点、事物或系统，反复地运用同样的规律来支配。

如方程：Xn=f（Xn-1）

问题：1.找一个函数的不动点，并确定它是否稳定？

2.如果没有不动点，是否存在周期点？

例如：f（X0）=X1

f(Xl)=X0

即有f（f（X0））=X0这时X0就是函数的一个2周期点。

如果从X=X0开始按照公式Xn=f（Xn-1）迭代n次回到原来地方，但迭代次数小于n时候都回不到原来地方，X0就叫做f（X）的一个n周期点。

一周以后，李天岩证明了：如果区间到区间自身的函数连续，且有一个3周期点，那末对于任何正整数n，f（X）有n周期点。也就是说：

只要有了3周期点，就什么周期点都会出现。

结果发表在《美国数学周刊》，题目“Period Three Implies Chaos”，首创Chaos（前人硬译为“混沌”）概念。学生和老师均由此做出了重要贡献。

【什么是混沌？】

确定性的方程存在内在随机性！确定的计算得出不确定的结果！

李天岩用Chaos（“混沌”）概括计算出现的结果，而不是Confusion（混乱）。预示世间存在一种先前难以捉摸、不为人知的性质。

混沌是自然界看似混乱的一种性质。

混沌是自然界的一种普遍运动形式。

自然界三种状态：有序、无序、混沌序。

【混沌有没有规律？】

[菲根鲍姆（Feigenbaum）的故事]

上世纪70年代菲根鲍姆博士毕业后，无固定职业，最后被他的老师带到洛斯阿拉莫斯实验室。他整天拿着计算器在实验室周围象幽灵一样转，痴迷于多年没有成果的混沌现象的思索。周围的人都担心他会得精神病，他的母亲更担心。

1978年，一天，菲根鲍姆给母亲写了一封信，信上说：“母亲大人，我马上就要成为世界名人了”，令母亲大吃一惊：“我儿真的得了精神病？”绝对不是。菲根鲍姆从地狱里走出来了，他得到了20世纪科学上的一个重大发现：对截然不同的函数进行迭代，在迭代过程转向混沌时，它们竟遵循同样的规律，都受到两个数字的支配。这两个数字就是：4.669201609……和2.502907875……

[菲根鲍姆常数]

d=4.669201609……

a=2.502907875……

d（倍周期分岔间距比值）和a（倍周期分岔宽度比值）统称菲根鲍姆常数。它们与p和e等常数一样，是一个与函数形式无关的普适常数。

【蝴蝶效应】

[洛伦兹（Lorentz）的故事]“某人打一个喷嚏会产生一场暴风雨吗？”

20世纪60年代马萨诸塞州理工学院的洛伦兹利用当时又大又笨的计算机计算气象。机器的可靠性很差，没有必要的速率和记忆。不过凭着他的智慧，成功地用比较简单的表述简化了气象学，用简单方程描述空气和水的运动，使机器通过计算可以机械地重复气象报表。但计算所要用的时间往往比较长。

1961年冬的一天，洛伦兹想继续计算过早中断的气象报表。为节约时间，不是从头开始而是从原计算的中途开始。他原以为新曲线会从老曲线中途出发，在老曲线附近1毫米处相重合。但结果使他惊呆了：新旧曲线在开头相随得很好，持续几个月后分离很快，以致一切有亲缘关系的表象都消失了。反复检查证明，计算机没出问题，仅仅是因为新一轮计算输给模型的初始条件省略了小数点后面第四位后面的值（当时计算机告诉他是0.145237，他偷懒只取了0.145）。只差小小的一点点，观看到两组天气模式与预计的截然不同。

洛伦兹悟出：计算如此，在真实的情况中也是如此，在大气层中总会有测不到的小动荡会增大，结果无法预测。所以，超过6或7天的预报毫无价值。

洛伦兹把内在随机性对初始值的敏感依赖形象地喻为“蝴蝶效应”：在巴西一只蝴蝶翅膀拍打能够在美国德克萨斯州产生一股龙卷风。

图4-4

一个初始的小改变引起了最终的巨大改变！这在决定性的经典科学中是不可思议的。洛伦兹遇到了真实的混沌。洛伦兹的发现预示了混沌科学的开始。

[蝴蝶效应应了一个民谣]

钉子缺，蹄铁缺；

蹄铁缺，战马瘸；

战马瘸，骑士绝；

骑士绝，战事折；

战事折，国家灭。

【洛伦兹方程——混沌的最早实例】

1963年，洛伦兹描写大气运动所用的微分方程组：

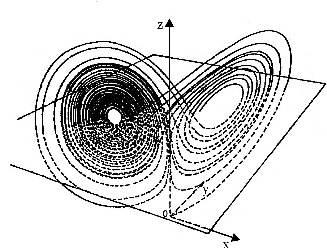
图4-5

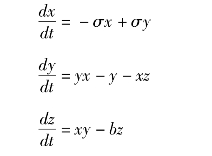
这是一个非线性一阶微分方程组。洛伦兹用计算机描述了系统在相空间轨线的图像，它是一个奇怪吸引子，也叫做混沌吸引子，由于洛伦兹的伟大发现，这个图像成为了混沌科学的标志。

【进入了非线性的世界】

不可捉摸的无序和不可预见的有序。

[内在随机性]

洛伦兹的水轮

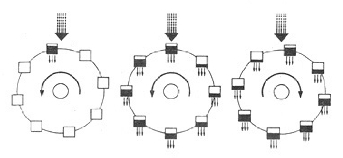
图4-6

水轮永远达不到恒定的速度，它一会儿正转，一会儿反转，不以任何可以预报的方式重复。

[涌现]

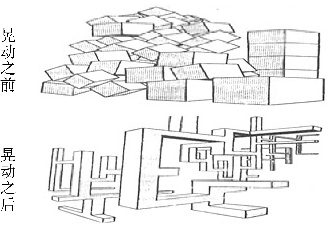
图4-7

一堆若干面带磁性的物体，被晃动之后，产生一种不可预知的结构，再晃动一次，出现另一种不可预知的结构。两次晃动的结果之间没有接续性。

三、让我们一起来发现混沌

【计算出来的混沌】

一个特别简单的模型（数学模型）会富藏着大量的动力系统的复杂性。

[迭代方程]

Xn+1=f（Xn）或　Xn=f（Xn-1）

特点：将前一次计算的结果作为后一次计算的自变量代入原方程计算，这样的运算可以多次反复进行。

[逻辑斯蒂方程]

Xn+1=λXn(1-Xn)

其中，变量X的范围在[0，1]区间，参数λ的范围在0＜λ≤4，这是一个二次方程，即非线性方程；可以利用一个方程组来替代并求出该方程的解：

y=x

y=λx(1-x)

解方程：x=0　x=1-1/λ

[画图]

（1）画直角坐标系XOY

图4-8

（2）在X轴取区间[0，1]，这是Xn的变动范围；在Y轴取区间[0，1]，这是Xn+1的变动范围

（3）作直线y=x的图像；作抛物线y=λx（1-x）的图像（先取定参数λ的值再作图）

（4）直线y=x与抛物线y=λx（1-x）的两个交点（O点和A点）是不动点，也就是方程组的解

[在图像上进行迭代计算]

（1）在X轴取X0　（要满足0＜X0＜1）

（2）在X0处作X轴的垂线与抛物线y=λx（1-x）相交，交点M0的纵坐标的值就等于λX0（1-X0），即X1

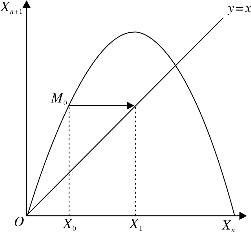
图4-9

（3）因为逻辑斯蒂方程Xn+1=λXn（1-Xn）迭代的性质是，第一次计算的结果与第二次计算代入的自变量的数值相等，所以我们可以通过直线y=x来确定下一次计算要代入的值。

（4）过交点M0作X轴的平行线，这条平行线与直线y=x相交，交点纵坐标的值就等于交点横坐标的值，即线段X0M0=OX1于是X1被确定。这是第一次迭代计算。

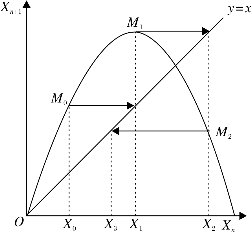
图4-10

（5）在X1处作X轴的垂线与抛物线y=λx（1-x）相交，得到X2，用同样的办法在X轴上确定X2于是完成了第二次迭代计算。

（6）如此继续下去进行n次计算，我们就会在X轴上找到一系列点，在迭代计算过程当中，有的点稳定，有的点不稳定，有的点是不动点。

（7）数学家发现，如果改变方程的参数λ的值（抛物线的形状随之改变），这些点的稳定状态也随之发生改变。稳定状态只与参数λ的数值相关，而与代入X的值无关。

[稳定性随参数而变]

注意　抛物线y=λx（1-x）图像的最高点是：当x=0.5时y=0.25λ

（1）当参数0＜λ＜1时，不动点O点是稳定的不动点。

图4-11

例如　当λ=0.8时，抛物线为y=0.8x（1-x），图像的最高点：y=0.25∗0.8=0.2，抛物线很矮。这时，利用图像进行迭代计算，多次迭代，收敛于O点。

（2）当λ=1时，O点不稳定。

（3）当1＜λ＜3时，O点不稳定，而A点是稳定的不动点，这时，给X一个初始值X1，迭代后收敛于A点。

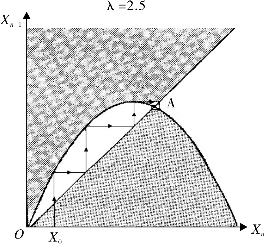
图4-12(www.xing528.com)

例如，当λ=2.5时，抛物线为y=2.5x（1-x），图像的最高点：y=0.25∗2，5=0.625，抛物线高度中等。这时，利用图像进行迭代计算，多次迭代，收敛于A点。

（4）当λ=3时，A点也不稳定了。

（5）当3＜λ＜3.449时，A点不稳定。然而，此时，生出一对稳定的2周期点B1B2。

图4-13

例如，当取λ=3.2时，抛物线为

y=3.2x(1-x)

图像的最高点：y=0.25∗3.2=0.8，抛物线比较高。这时，利用图像进行迭代计算，多次迭代，得到两个2周期点：

B1点为x=0.513

B2点为x=0.799

这时，0.799=3.2 ∗0.513 ∗（1-0.513）

0.513=3.2∗0.799∗(1-0.799)

（6）当λ=3.449时，2周期点B1B2也不稳定了。

（7）当3.449＜λ＜3.545时，2周期点B1B2不稳定。然而，此时，生出四个稳定的4周期点C1C2C3C4。

例如，当取λ=3.5时，

C1点为x=0.152；C2点为x=0.879；C3点为x=0.373；C4点为x=0.823

这样的过程继续发生，得到8周期点、16周期点……

图4-14

（8）当λ>3.57时，就会“分岔”出无穷周期序列C1C2C3……Cn它们似乎是分布在[0，1]区间上的随机数。这就是混沌。

例如，当取λ=3.8时，抛物线为y=3.8x（1-x）的图像的最高点：y=0.25 ∗3.8=0.95，抛物线很高。这时，利用图像进行迭代计算，多次迭代，进入混沌状态。

[无花果树]

图4-15

上述过程称为倍周期分岔。它象一棵不断生长的无花果树。从一条简单的轨线通过周期倍增分岔发展成为无数条关系复杂的轨线。

倍增分岔过程受菲根鲍姆普适常数支配。

Δm=λm-λm-1

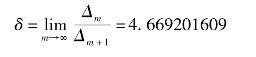
四、条条道路通混沌

【倍周期分岔进入混沌】

一个原来具有周期性行为的系统，在一定条件下，经过周期加倍，会逐步丧失周期行为而进入混沌。例：非线性电子电路随输入压增加，输出压的频率会经历二分频，四分频，八分频，十六分频……，各种频率，互相套叠，进入混沌。

【阵发混沌】

在非平衡非线性的条件下，某关键参数的变化达到一定的临界阈值时，系统就会时而有序时而混沌的随机震荡。若参数变化超过阈值，系统由振发混沌进入完全的混沌。

【不同频率耦合出现混沌】

三体相互作用会进入混沌。“茹勒一泰肯”证明，三个（包括三个）以上互不相关的频率耦合时，系统必然形成无穷多个频率的耦合，出现混沌。“道生一，一生二，二生三，三生万物”。

五、揭开混沌的秘密

【相空间和奇怪吸引子】

[庞加莱的故事]“鹰一样的视野：上帝他是不是也玩骰子？”

牛顿年轻时发现万有引力、无穷小计算和光的性质，从而改变了宇宙的面貌。但是几十年后在研究月球运动中遭到厄运，三体运动困扰了牛顿整整一年，没有得到成果。牛顿后来寻找上帝去了。

庞加莱27岁时已成为巴黎大学数学教授，是他那个时代的最伟大的数学家之一。斯德歌尔摩大学为庆祝瑞典和挪威的国王奥斯卡二世60岁诞辰而组织了一次数学竞赛。比赛题目之一涉及太阳系的稳定性，也就是困扰牛顿的那个三体（多体）问题。庞加莱引人注目地接受了这个“1000法郎的问题”的挑战。

庞加莱天才地使用了一种新的视野——“相空间”，后来人们把它比作鹰的视野（人们不知道鹰是怎样准确地盯住飞快运动着的猎物的），第一个发现了天体运动中的混沌，成为混沌理论的先驱，并由此引发了一次动力学革命。他发现：上帝并没有把一切都安排得头头是道，精确无误，混沌就存在于牛顿决定论的方程组的同一核心中。

[相空间]

相空间，即“状态空间”或“抽象多维空间”

一个状态用一组（n个）指标值描写，每个指标取不同的值，得到不同的指标组，描写事物的不同状态。一组（n个）指标值作为一个“点”，无限多个“点”构成了一个n维“空间”。这个“空间”中的一个“点”对应于一组（n个）指标值，也就是事物的一个状态。这个“空间”就是状态空间。优点：尽管被研究的系统很复杂，背景怪异，因素众多，但在抽象空间中单一的点足以表示一个系统的全体。

例如：对于三体问题而言（月亮、地球、太阳相互运动），为了有三体的全部景象，需要一个18维空间（位置、速度=6维；三体×6=18维。即有9个方位坐标，9个速度坐标）。借助这个大维数，我们可以对所有因素同时发生的景象一览无遗。在多维空间中，整个太阳系只用单一的点来表示，而不是在通常三维空间中的10个点。

[相空间的流]

于是，事物状态的变化可以被描写为“相空间”中“点”的变化，事物状态的连续变化就表现为“点”在运动——“点”在“相空间”中画出一条曲线。这条曲线称为“相空间中的流”。

[吸引子]

“吸引子”是相空间中的点集（点的集合），它能够把近旁的“流”都紧紧地吸引到它的身上。通俗地说，就是，系统以某种状态开始变化，最终会达到系统所偏爱的某种状态，如果没有别的因素向它施加作用，它会保持在那个状态中。在上述迭代计算中，稳定的n周期点就是吸引子。

[普通吸引子]

例如：零维的吸引子是个不动点；一维吸引子是个极限环；二维的吸引子是个环面；……

[奇怪吸引子]

如果吸引子以相似的集合形式出现，并且集合中任意两个成员间又是分开的。这种吸引子叫做奇怪吸引子。

[相空间里的混沌区]

整个混沌区是稳定的，但区内却是活跃易变的。区内两个靠得很近的点，随时间推移，对边界条件依赖极为敏感，会指数发散开，无法用“轨道”概念的描述方法预测未来行为。所以奇怪吸引子也叫混沌吸引子。

图4-16

[一个系统的动力运动状态可以用两种不同的方式表示]

古典方式在于表示作为时间函数的系统演化（上一行的图形）。

现代方式在于研究在相空间中系统动力状态的一个点的轨迹（下一行图形）。

系统（a）在多次振荡之后收敛于平衡状态，这与在相空间中许多环形线收敛于一点相对应。

系统（b）周期性重复，这与在相空间中一条循环轨道相对应。

系统（c）具有相同周期的运动，但较复杂。它仅在三次不同振荡后进行重复，人们称它具有3周期的循环。这与相空间中较复杂的环形线相对应。

系统（d）是混沌系统，在相空间中具有洛伦兹奇特吸引曲线的蝴蝶翅的形状。

[庞加莱截面]

n维相空间中的流线（轨迹）很复杂，描写这些流线的微分方程是非线性的，写不出数学形式的解。

图4-17

为了研究相空间的流线（轨迹），庞加来想出了一个办法。由于系统的状态随时间连续变化，故描写系统状态的相空间中的点随时间连续变动，所以反映相空间中点的连续变化的流线有前进的方向。

于是，庞加莱得到了方法：用一个n-1维的“平面”（应该称为“准平面”，它比相空间少1维）切割这条流线。

右图表示在3维相空间中的一个庞加莱截面（是个平面，它是2维的几何图形），它与流线相交于点P0、P1、P2、……，

因为流线有前进的方向，所以交点就有顺序：P0→P1→P2→……，即，从P0得到P1，从P1得到P2，……，这就有了“迭代”的意思，可以用迭代的手段研究这些交点的性质，从而研究流线的性质。

图4-18

庞家莱截面是绝妙的研究方法。

如果流线的运动是周期运动（是一个闭合的圈），则截面上就是一个不动点。

如果流线是四次重复的循环运动（缠绕四次才闭合的圈），则截面上是4周期点（有四个不动点）。

[利用截面技术庞加莱在1888年就发现了混沌和奇怪吸引子]

庞加莱利用他的发明研究天体运动的时候，发现了在垂直平面内的秘密：三体中一个天体的位置中或初始速度中一个很小的改变就可以完全改变其轨道，这一小的改变可以使它失去稳定的平衡进入混沌。

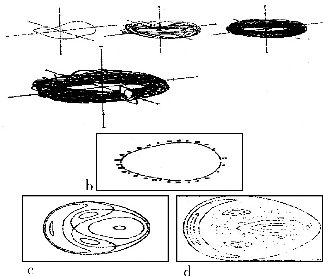
图4-19

月球，地球，太阳都受牛顿万有引力同样精确而有强制性的一条定律支配，相等地给出不可预见的地方和不确定的地方，一点小小的偏差，系统就可能失稳进入混沌——决定论中的测不准。

恒星轨道在相空间内划出复杂的轨迹。如果恒星的动能不超过临界值，恒星轨道稳定（b、c）。如果恒星的动能超过临界值，恒星的轨道变成混沌的轨道，而且稳定区和混沌区相互交错（d）。发现奇怪吸引子现象。

【混沌区域中的有序之窗】

图4-20

[迭代吸引子混沌区]（相控图）

混沌并非完全无序。把混沌中的一部分拿出来放大，发现它们同全体很相似，混沌内部也是有结构的。

在混沌区中有无数有序之窗，如同每一瀑布层中有无数分叉一样。每一个窗中吸引子都有一个特征性周期。

在总体上看似乎混乱，但各局部是有规律的，有多种可能甚至无数种可能，哪种可能将成为现实，没有周期性，不可预言。

混沌显示了一种“非周期性的确定性”的规律

【混沌运动的特征】

（1）内在随机性

（2）对初值的敏感依赖性

（3）奇异性

（a）从整体上看，系统是稳定的；但从局部看，吸引子内部是不稳定的，相邻运动轨线互相排斥，按指数速度分离。

（b）混沌吸引子有无穷层次的自相似结构。

（c）它的空间图形具有分形的几何结构，其维数一般是分数维的。

【事物变化之规律】

（1）稳定→不稳定→新的稳定

（2）有序→混沌→有序

（3）平衡→不平衡→新的平衡

六、自组织

【问题】

世上的各种事物，是怎么形成的？

不要上帝插手，不由外部，也不由内部控制的指令，一个有组织有序的系统如何自发地的完成其形成过程？

【一些基本概念】

可逆和不可逆

有序和无序

熵与信息

稳定与不稳定

对称和破缺

时间之矢和不可逆性

序参量和超循环

内在随机性，涨落和突变

【热力学第二定律与达尔文进化论的矛盾】

[热力学第二定律]

熵增定律。对于一个孤立体系（与外界无能量交换的封闭系统）熵总是趋向增大。一切有序的东西都因热力学平衡而化为无序的东西。世界的衰退，向极度混乱是必然的趋势，是不可逆的。这是我们从热力学理论推出的事实。

[进化论]

生物从无到有，物种由少到多，从简单到复杂，从低级到高级，到意识的产生。有新生事物产生。这是我们看到的事实。

[不可逆作用]

严格来说，自然界发生的一切过程都是不可逆过程。

现在已经明白：不可逆过程如果发生在近平衡态附近，那么它的作用的确导致系统有序结构的破坏；如果不可逆过程发生在远离平衡的非线性非平衡区，加上其它条件，那么，它就有重要的建设作用。

图4-21

[耗散结构]

一切有序、有结构的东西都是物质、能量、信息流中的漩涡。

[耗散结构进化中的宏观非决定性]

【系统自发地从无序到有序进化的条件和依据】

（1）必定发生在远离平衡的非线性区（远离热平衡的系统）。耗散结构理论研究的结果表明“非平衡是有序之源”。

（2）必须是开放系统。系统从外部输入的负熵流大于系统内部的熵增。

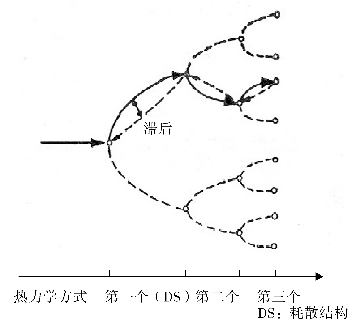
图4-22

（3）必须存在非线性相互作用。这种作用使各要素产生相干效应，使杂乱变成有序，产生质变。该作用还可使系统产生多个可能的分布，产生不同的新结果。

（4）必须有正反馈机制（催化、超循环等），使系统的变化被放大和加剧。

（5）系统经由内在随机性导致涨落（偏离平均态），在某个临界点附近被放大，产生质变。从无序到有序或从一种有序到另一种有序。