三种方法：语言模型方法、数学模型方法和计算或算计模型方法

至今，社会研究获得的唯一真正的成果就是：社会研究还没有成果。因为，攻克“社会复杂性”的有效武器还没有找到。

力图把握和克服社会真实的复杂性（the real complexity of reality）即跨层次的相互关系的认识手段实际有三种，按出现先后次序，分别为：语言模型方法，数学模型方法，和计算或算计模型方法。

首先是语言模型方法。

主要是通过语言描述的方式展开。这是目前社会学或社会科学研究中最常用的方法，其优点是灵活。研究者可随时根据需要改变对象，改变目的和改变结论。而且，使用的语言越抽象，越经得住时间和空间变化的考验，当然也就越模糊、越空洞。其中的奥秘经由维特根斯坦发现：真实的世界本来就不能被言说。语言是万能的，但同时也是无能的。社会学或社会科学所构建的模型，一般都由自然语言组成，自然语言所设定的那些条件通常都很模糊，往往无法与现实对应：要么在现实中没有，要么隐喻含糊，要么说东指西。在众多这样的研究者中，有一个人，他的成果例外，就是亚当·斯密和他的《富国论》。《富国论》是关于社会系统复杂性的最早、最系统的代表著作。亚当·斯密将社会复杂性比喻为一只看不见的手，通过这只神秘的手，众多社会成员利己的社会行为催生了界定清晰的社会秩序。社会“自然而然”成为有序系统。

其次是数学模型方法。

其优点是精确，通过函数、概率，依既定目标设计模型；通过设计把握社会复杂性，通常称为社会系统工程方法。其步骤包括：目标、工具利用、设计、可行性分析和优化。该方法突出的要点是“设计”，绕过周期性，规定确定性。它允许我们精确地定义一组现象，然后使用一套标准的求解方法解决由此产生的系统。前提是，我们需要足够纯净的模型组件。就其设计结果来说可以做到精确和最优，例如，阿波罗计划。不过，我们知道，当把数学模型方法运用到以社会为研究对象的时候，由于对社会过程和现象作精确量化是非常困难的，除非牺牲细节，忽略例外，变动态为静态并假定对象同质性、平均化。如此一来，精确、漂亮、确定性十足的设计模型也就与社会实际存在和变化相距甚远了。不乏看到，经济学、社会学中许多漂亮但无实际价值的设计模型。尽管如此，数学模型方法依然是目前认识社会现象的重要手段，不否定它们在社会研究中的价值，也不排除它们的局限性被不断克服的可能。

(www.xing528.com)

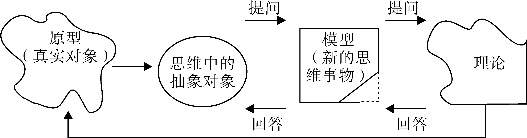
图3-5　模型方法的应用^[2]

第三种方法，作者把它叫做“计算-算计模型方法”

社会过程及事件，其表现形式如同生命，是活的，而且要比单纯生物集合（生物社会）更加复杂。社会系统中“多”和“一”的对应或确定关系，依传统的科学探索方式，难以得到全部可能为真的结果。大数据时代一种被认为最原始、最笨、最容易操作的认识和把握社会过程和事件的方式应运产生，这就是所谓“社会生活计算模型方法”，或称为“基于主体对象的模型方法”^[3]，用最简单不过的计算方法（运用计算机），对社会（由局部映射总体）进行模拟，立足于社会成员及组织主体，基于一定智力水平上的相互关系，自下而上，至始至终，重现社会过程和事件，将一个一个可能真实的过程和事件显现出来。该方式颠覆了近代开始以来的科学方法论路线，回到人类认识的起点。研究者同研究对象的关系如同下棋，棋盘上的每一个棋子都是活的主体，具有处理信息能力，同时与其他主体发生交互。研究者甚至也成为棋子中的一员，亲临过程，参与其中。

计算模型方法，实际上就是老百姓说的“算计”。孙子曰：“多算胜，少算不胜，而况于无算乎？”（孙子兵法）。但是在大数据时代到来之前，算计只能用于极有限范围的过程和事件，“走一步看三步”，三步之外所发生的事情一般就只能靠猜了。于是就有了经传统至现代的科学研究认识论和方法论。函数、方程、统计与概率等工具应用的目的都为征服（克服）“真实世界中真实的复杂性”。真实世界中真实的复杂性，因为数理模型的精确性、静态性、最优化、抽象，及同质性与对称性等要求，在结果中消失掉了。面对现实，这种一劳永逸解决问题的认识论和方法论模式，除了耗费研究人员的精力之外收效甚微。当然，也不能否定传统工具的应用对人们认识社会及其具体事件有着重要的启发作用。

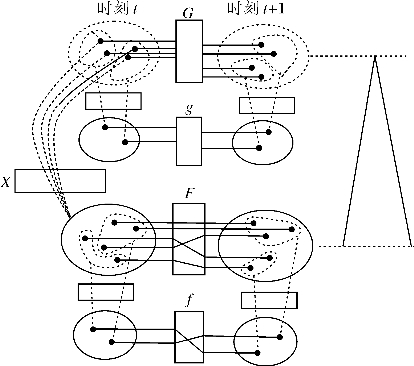
图3-6　理想的建模与看不见的手：X、F、G

从被动地对待研究对象（观察、实验、理想化建模）转换为使用基于主体的对象，是计算（算计）模型方法的基本要点。它比较切合实际的认定社会是一个众多具有主体地位的社会成员，通过交互而适应的系统。该模型充分显现主体交互适应过程，择取语言模型的灵活性和数学模型的精确性，代表一种权衡。研究人员看不见亚当·斯密所比喻的那只“看不见的手”，但是却感觉到这只手在工作。