便携式不触地书桌的制作与实现：机械原理和杠杆原理的应用

张诗泉

（一）项目提出

我在上课时遇到过有老师来听课却没有桌子的情况，所以他们只能把书摊在大腿上书写笔记（如图4-25），这样书写很不舒服，而且影响书写质量，很不方便。类似的情况不止在教室里有，在生活的许多场合里也很常见。于是我想，有没有一种可方便携带的桌子能解决这个问题呢？在网络搜索无果后，我结合自己生活中见过的其他桌子（如图4-26，它的桌子没有接触地面），决定自己制作可折叠的不触地书桌。

图4-25　老师教室听课现状

图4-26　现有的不触地书桌

（二）研究目的、思路、过程

研究目的：用机械原理制作可折叠的不触地书桌。

设计模型：在多次设计后，我确定了这样的结构（如图4-27）。

桌面面积45cm×30cm，抽屉部分桌面：15cm×30cm，支撑板面15cm×30cm，坐垫面积33.5cm×30cm。

几何证明部分：在构建3D模型时，我遇到了一个问题，即在模型里有一条支撑杆的长度不知道。于是我构建了如图4-28的数学模型，把AE设为支撑杆，可绕E旋转。这就把问题转换成在直角三角形ABE中，求AE的长。

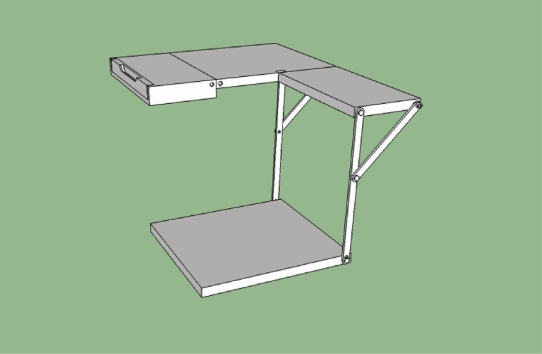
图4-27　不触地便携书桌3D设计图

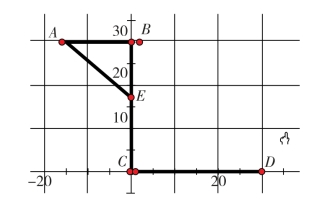
图4-28　不触地便携书桌几何证明图

如图AB=BE=13cm，∠B=90°

于是，在直角三角形ABE中，用勾股定理（a2+b2=c2）可得：

∵在Rt△ABE中，AB=BE=13（cm）

∴AB2+BE2=AE2

132+132=AE2

AE≈18.4（cm）

支撑杆长18.4cm

模型构建：在得到了相关的零件数据后，我构建了如图的3D模型，如图4-29。

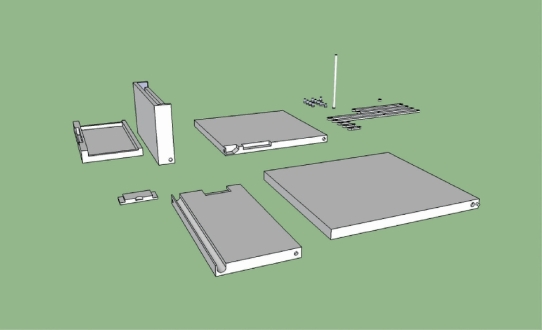
图4-29　不触地便携书桌3D零件图

将零件组合，可以模拟出使用时的展开过程，如图4-30、图4-31。

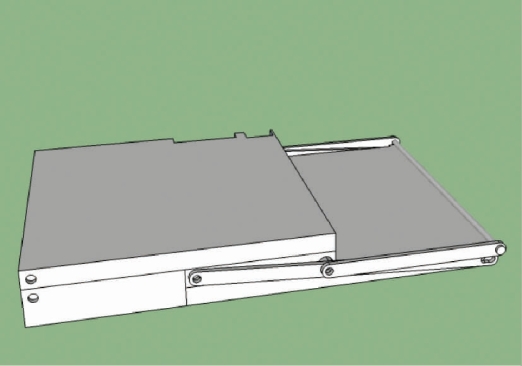
图4-30　不触地便携书桌折叠3D图

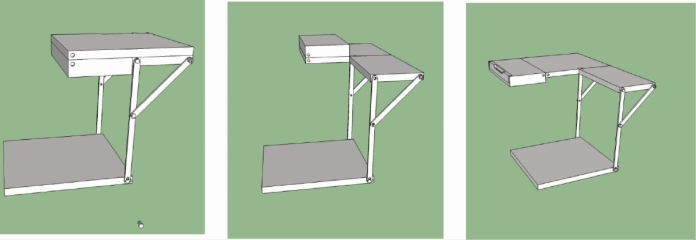
图4-31　不触地便携书桌分步展开3D图

（三）物理证明

在构建出3D模型后，为了证明我的方案可行，并且计算出桌子实际的承重能力，我决定用我学过的知识来证明并计算它。

通过请教老师与上网搜索，我通过悬挂法测量相似模型的重心，把实际成品的重心估算了出来，重心离边缘0.09m。

经过考虑，决定使用悬挂法。我找到了一根细绳，在小模型上找一点，用绳悬挂，画出其静止后的重力线。同理再找一点悬挂并画出重力线，两条重力线的交点就是桌子重心的大致位置。

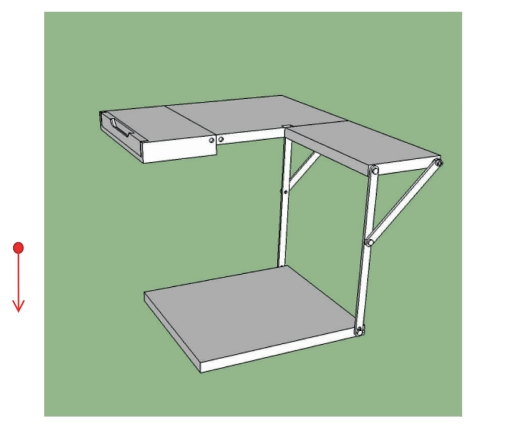
图4-32　不触地便携书桌重心大致位置

找到重心后，我使用杠杆原理来证明，并且将桌子简化为以下杠杆。

其中G1为坐垫与使用者重之和（G板+G人），G2为桌板与承载物体重之和（G板+G承）；O为支点，AO为动力臂（L1=15cm），G2到O的距离OH为阻力臂（L2=9cm）。(www.xing528.com)

由于桌面打算使用木质材料制作，所以桌子密度取500kg/m3，桌面体积为0.0045m3，坐垫体积为0.0009m3。

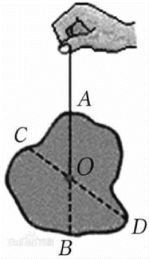
图4-33　悬挂法基本原理与操作

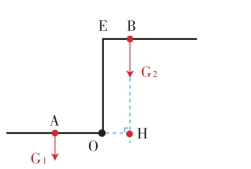
图4-34　杠杆简图

根据ρ=m/V推导得：

m1=ρ·V1=500kg/m3×0.0045m3=2.25kg

m2=ρ·V2=500kg/m3×0.0009m3=0.45kg

根据G=mg（g取10N/kg），推导得：

G1=m1g=2.25kg×10N/kg=22.5N；G2=m2g=0.45kg×10N/kg=4.5N

由于使用时作用在坐垫上的主要是使用者躯干对其的压力，根据资料，我得知人体躯干占身体重质量约77%。一个10岁的健康男孩质量约为30kg（这里我参考一同学的兄弟的相关数据），那么当他作为使用者时，其躯干对坐垫的压力视为其躯干所受到的重力：

G躯干=m躯干g=77%×30kg×10N/kg=231N

因此杠杆中的G人=G躯干=231N

如此得到数据后，我就可以计算出桌子的承重能力（G承）了。

由杠杆原理（F1·L1=F2·L2）得：

G1·L1=G2·L2

（G人+G1）·L1=（G承+G1）·L2

G承=（G人+G1）·L2÷L1-G1

G承=（231N+4.5N）×0.15m÷0.09m-22.5N

G承=370N

G=mg推导得m承=G承/g=370N÷10N/kg=37kg

即当使用者重30kg时，桌子最大承重为37kg

同理使用这个方法，我要证明方案可行，就需要证明G板与L1之积等于G板与L2之积。

G板·L1=4.5N×0.15m=0.675，

G板·L2=22.5N×0.09m=2.025，

因为0.675＜2.025，所以桌子不能达到平衡。

为了解决这个问题，我决定在坐垫这边增加一个配重，给坐垫底部加上一层0.003m的底板。为了使整个桌子平衡，这块底板需要：

G底=G板·L2÷L1-G板=22.5N×0.09m÷0.15m-4.5N=9N

所以底板质量为0.9kg，已知体积设为0.000135m3

所以ρ底=m底/V底=0.9kg÷0.000135m3≈6.7g/cm3

根据资料我知道，钢的密度为7.85g/cm3，大于所需密度，因此桌子的底板使用钢材是合适的。当这样改进后，桌子便能平衡地立起来。

综上所述，当桌子使用钢木结合的材料制作的话，就能够立起并且能够承重37kg。

（四）项目与同类产品对比

表4-7　产品特点对比表

（五）项目创新点与作品应用领域

本项目最大的创新点是抛弃了原始折叠桌用地面做支点的方式，把支点转移到坐垫上，实现不触地。本项目用于满足人们在各种只有椅子没有桌子的情况下需要写作的需求，可折叠性使折叠桌更适合户外携带。

本项目将来可以设计在普通椅子上，使其成为带折叠桌子的椅子，用于班级或其他场合，且便于整理堆叠。