计划工作最全面的分析方法之一,就是运筹学,它是“管理科学”理论的基础。运筹学是一门研究如何有效地组织和管理人机系统的科学,作为一门学科,它诞生于20世纪30年代末期。运筹学一词在英国称为Operational Research,在美国称为Operations Research,缩写为OR。在《大英百科全书》中,“运筹学是一门应用于管理有组织系统的科学”,“运筹学为掌握这类系统的人提供决策目标和数量分析的工具”。就内容讲,运筹学又是一种分析的、实验的和定量的科学方法,用于研究在物质条件(人、财、物)已定的情况下,为了达到一定的目的,如何统筹兼顾整个活动各个环节之间的关系,为选择一个最好的方案提供数量上的依据,以便能为最经济、最有效地使用人、财、物做出综合性的合理安排,取得最好的效果。
运筹学实际上起源于20世纪初叶的科学管理运动。像泰罗和吉尔布雷斯夫妇等首创的时间和动作研究,甘特发明的甘特图,以及丹麦数学家爱尔朗1917年对丹麦首都哥本哈根市电话系统排队问题的研究等,应当看作是最早的运筹学。第二次世界大战中,为适应战争的需要,发展出了现代运筹学的一个最成熟的分支——线性规划。随后,随着计算技术的进步和计算机的普及,非线性规划、动态规划、整数规划、图论、排队论、博弈论(对策论)、库存论、模拟等一系列重要分支也逐步发展和完善起来。
在计划工作中应用运筹学的一般程序,常按以下步骤进行。
(1)明确问题。通过调查和分析,将所要解决的问题弄清楚,包括问题所在、要求目标、限制条件、假设前提、可能的各种决策方案等,在此基础上把问题明确地表达出来。
(2)建立模型。模型是客观事物的一种映象,它既要反映实际,又要进行抽象而“高”于实际。建模是一种创造性活动,是非常重要的一步工作。很多实际系统往往非常复杂,因而在建模时必须结合实际情况进行认真的分析。建模工作包括拟定变量和参数,建立目标函数和正确写出约束条件等。
(3)模型求解。根据模型的性质和结构选用适宜的方法求解。如没有合适的现成方法,也可用随机模拟或构造启发式算法等手段寻求问题的“近似解”,解的精度由决策者确定。
(4)解的检验。检查求解过程有无错误,结果是否与现实一致。如出现问题,要分析问题所在,必要时修改模型或解法。
(5)解的实施。对实际问题来说,求出的解往往就是某种决策方案,要考虑具体实施中可能遇到的问题,以及实施中需要的修改。
上述过程有时需反复进行。
最典型的运筹学方法是线性规划法,另外,像非线性规划、整数规划、动态规划、图论、排队论、库存论等方法也已广泛应用于计划工作。
下面我们通过一个例子简单地了解一下线性规划问题及其模型。线性规划是运筹学中数学规划的一个分支,是运筹学中最重要的一种数量方法。主要用于研究解决有限资源的最佳分配问题,即如何对有限的资源做出最佳方式的调配和最有利的使用,以便最充分地发挥资源的效能去获取最佳经济效益。(https://www.xing528.com)
线性规划模型包括三个部分:①变量,它是线性规划模型中待定的对决策目标的实现有决定性影响的因素,一般用Xij或Xi表示;②目标函数,它是决策目标的量化,是变量的函数,如利润最大化、成本最低化等;③约束条件,它是实现决策目标的限制性条件,如市场需求的限制、可供资源的限制等。
有了变量、目标函数、约束条件,线性规划模型也就建立起来了。
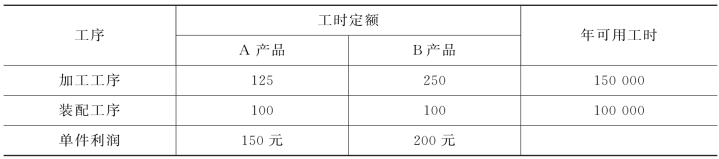
【例3-1】 某企业计划生产A、B两种产品,需要经过加工和装配两道工序。生产的有关资料见表3-1。问如何制订A、B两种产品的生产计划,才能使企业获利最大?
表3-1 某企业生产A、B两种产品的有关资料
【解】 设A、B两种产品的计划产量分别为x1、x2,我们可以建立该问题的线性规划模型如下:
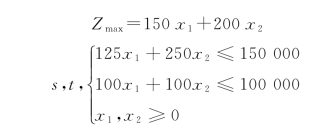
此线性规划模型可以用图解法和单纯形法求解,也可以通过使用计算机软件包进行求解,该问题的最优解是:
x1=800(件),x2=200(件),Zmax=160 000(元)
即该企业生产A产品800件,B产品200件时,获利最大,最大利润为16万元。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




