“找次品”是人教版《义务教育课程标准实验教科书数学》五年级下册“数学广角”的内容,它包含两个例题,都是要求学生利用天平在所有待测物品中找出唯一一个外观与合格品完全相同,只是质量有所差异的次品,并且事先知道次品比合格品轻或重.
“找次品”的教学,旨在通过“找次品”渗透优化思想,让学生充分感受到数学与日常生活的密切联系.优化是一种重要的数学思想方法,在教学中尝试把这种思想方法通过学生可以理解的简单形式,采用生动有趣的事例呈现出来,并运用它有效地分析和解决问题.让学生通过观察、猜测、试验等方式感受解决问题策略的多样性,在此基础上,通过归纳、推理的方法体会运用优化策略解决问题的有效性,感受数学的魅力,培养观察、分析、推理以及解决问题的能力,并学习用直观的方式清晰、简洁、有条理地表示逻辑推理过程,构建出解决这一类问题的数学模型.
本单元分两个内容编排:从3 件物品中找出1 件次品(轻一些),初步认识“找次品”问题,了解找次品的基本思路;从9 个零件中找出1 个次品(重一些),探索找次品的一般方法(即模型).
例1:有3 瓶钙片,其中一瓶少了3 片(次品).你能设法把它找出来吗?
例1 从最简单的问题(3 瓶钙片)入手,让学生讨论找次品的方法,通过交流聚焦到用天平来找次品的方法上来.通过用天平直观演示,说明基本推理过程:如果天平平衡……,如果天平不平衡……(见图9.2.4).接着通过提问:“你能想办法把用天平找次品的过程,清楚地表示出来吗?”引导学生用直观方式记录找次品的思维过程.需要明确用天平找次品,并不是一定要通过天平称,而是利用天平平衡原理,通过逻辑推理确定出次品,因此教师可以引导学生用格式大致统一的直观图或流程图辅以文字说明来记录和推导.当然,学生也可以用不同的表示方法,但一定要合理.
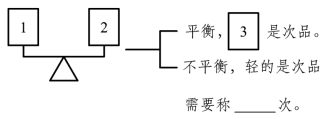
图9.2.4
例2:9 个零件里有一个是次品(次品重一些).假如用天平秤,至少秤几次能保证一定找出次品?
有了例1 的基础,学生已经知道找次品的基本推理思路,在让学生理解了“至少称几次能保证找出次品”的含义后,直接提出“你们打算怎样表示找次品的过程?”可采取以下措施:一是让学生将推理的过程用直观、简洁的方式表示出来,并用“直观图”示例引导(见图9.2.5);二是让学生把不同的方案记录在表格中,以便进行分析、猜测(见表9.2.1);三是通过问题给出探索的线索,找出称量次数最少的方法.

图9.2.5(https://www.xing528.com)
表9.2.1 方案表

观察完成的表格,问:你发现了什么?(1)分成的份数、分的方法与找出次品所要称的次数有什么关系?(2)怎样分找出次品需要称的次数最少?最后要求学生用发现的方法找出10 个、11 个零件中的1 个次品(次品重一些),看看是不是保证找出次品的称量次数也是最少的.学生通过归纳、验证,概括出找次品的最优方法(即模型):把待分物品平均分成 3份,不能平均分的,也应使多一份的与少的一份相差1;根据物品的个数决定称的次数,其规律是:
2~3 个物品称1 次;
4~9 个物品称2 次;
10~27 个物品称3 次;
28~81 个物品称4 次;
……
找次品的思维模型:大于3n-1 或等于3n 个物品,需称n 次(n≥1).
“数学广角”中模型无处不在.学生学习数学知识的过程,实际上就是对一系列数学模型的理解、把握的过程.教学中,重视渗透模型化思想,帮助小学生建立并把握有关的数学模型,有利于学生把握数学的本质.因此在“数学广角”的课堂教学中,逐步培养学生数学建模的思想,形成学生良好的思维习惯和应用数学的能力.小学生对数学模型思想的感悟、体会和建立,不像某些数学知识的掌握那样可以立竿见影,需要教师在教学中逐步渗透和引导学生不断感悟,让学生经历数学建模过程,不断感悟数学模型思想,通过建立数学模型来解决实际问题.
小学数学教学非常重视数学模型思想,希望老师们开展相关的课堂教学的实践研究,为解决上述问题贡献智慧和经验.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




