“植树问题”是人教版《义务教育课程标准实验教科书数学》五年级上册的内容,它包含三个例题,主要是渗透有关植树问题的一些思想方法,通过现实生活中一些常见的实际问题,让学生从中发现一些规律,抽取出其中的数学模型,然后再用发现的规律来解决生活中的一些简单实际问题.教材以“猜想试误—合作探究—发现规律(建立模型)—深化规律(再次建模)—解释运用”为主线,渗透数形结合的思想,建立数学模型,发现问题实质,为后面解决问题奠定了坚实的基础.
本单元通过一些生活中的事例,让学生根据不同的情况总结出规律,并利用这些规律解决问题.但是,本单元教学的最终目的并不只是让学生明白规律,而是要引领学生进一步探究规律的产生原因,帮助其建立“一一对应”的思维方式,形成解决问题的策略,从而体验数学思想方法在解决实际问题中的应用.
在“植树问题”中最重要的数学思想就是模型思想,而如何让学生理解从实际问题中抽象出数学模型的过程是教学“植树问题”的难点.为了突破这一难点,教材突出了线段图的教学,通过几何图形等直观帮助学生理解“植树问题”的数学模型.
例1:同学们在全长100 米的小路一边植树,每隔5 米栽一棵(两端要栽).一共要栽多少棵树?
例1 是探讨关于一条线段并且两端都要栽的植树问题,让学生通过画线段图来发现栽树的棵数和间隔数之间的关系(见图9.2.1).通过这两幅图,让学生把“点”(树)与“线”(间隔)一一对应起来,结果发现还多出一个“点”(树),所以构建出“两端都栽”的模型:“栽树棵数=间隔数+1”.
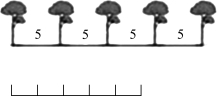
图9.2.1
例2:大象馆和猴山相距60 米.绿化队要在两馆间的小路两旁栽树(两端不栽),相邻两棵树之间的距离是3 米.一共要栽多少棵树?(https://www.xing528.com)
例2 通过迁移呈现出两端都不栽的线段图(见图9.2.2),所以构建出“两端都不栽”的模型:“栽树棵数=间隔数-1”.“做一做”部分的第2 题让学生通过迁移画出一端栽另一端不栽的线段图.
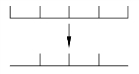
图9.2.2
例3:张伯伯准备在圆形池塘周围栽树.池塘的周长是120 米,如果每隔10 米栽一棵,一共要栽多少棵树?
例3 则让学生理解在封闭曲线上植树的线段图(见图9.2.3)的画法以及它和一条线段上植树中的一端栽另一端不栽的联系,所以构建出“只栽一端”的模型:“栽树棵数=间隔数”.接着再用抽象出来的模型解决一般性的问题,最后再迁移、变通.教材整个单元通过线段图的教学,突出“一一对应”的思想,并以此为基础分析植树问题三种不同的情况,即“两端都栽”“两端都不栽”与“只栽一端”.无论哪种情形,都能用“一一对应”的思想统领.

图9.2.3
教材通过选取生活中不同的事例,让学生体会一种在数学学习、研究问题上都很重要的数学思想方法──化归思想,使学生感悟到应用数学模型解决问题所带来的便利.同时培养学生在解决实际问题中探索规律,找出解决问题的有效方法的能力,初步培养学生抽取数学模型的能力.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




