小学数学模型建构：深入理解广角中的'植树问题'和'抽屉原理'

数学模型思想是指对于现实世界的某一特定对象，从它特定的生活原型出发，运用观察、实验、操作、比较、分析、综合概括等方法，得到简化和假设，它是把生活中实际问题转化为数学模型的一种思想.

模型思想与很多课程目标点密切相关，如数感，符号意识，几何直观，发现、提出问题能力，数学的联系，数学应用意识，改善数学学习方式，等等.在教学中突出模型思想有利于学生更好理解、掌握所学内容.

“数学广角”主要是通过简单的事例向学生渗透一些重要的数学思想方法，从中发现规律，抽取出其中的数学模型，然后再用所学习的知识和方法来寻找解决问题的策略.在这里，我将结合自己对课程标准和教材的解读，谈谈对小学数学广角中的“植树问题”和“抽屉原理”的模型思想建构.

1.关于“植树问题”

植树问题是人教版《义务教育课程标准实验教科书数学》（2013 版）五年级下册106～111 页“数学广角”中的教学内容.它包含了数学中的植树问题模型思想、化归思想、对应思想、数形结合思想和转化思想.“植树问题”的教学涉及两种层面的数学活动：其一，“植树问题”可区分出三种不同的数学模型，即“两端都种”“只种一端”与“两端都不种”；其二，以“植树问题”为原型引出普遍性的“间隔现象”的思考模式，然后再利用这一模式去解决各种新的实际问题，如“路灯问题”“排队问题”“锯树问题”“爬楼问题”等.教材将“植树问题”按照“两端都栽”“两端都不栽”“只栽一端”三种情况依次呈现出来，通过对3 个例题的教学，使学生经历将实际问题抽象出数学模型的过程，掌握植树问题中棵数与间隔数之间的关系，并能利用这一关系解决简单的新的实际问题.

（1）植树问题的教学目标.

① 引导学生通过观察、猜测、试验、推理等活动，初步体会植树问题的模型思想.

② 通过画线段图初步培养学生探索解决问题有效方法的能力.

③ 让学生尝试用解决植树问题的方法来解决实际生活中的简单问题，培养学生解决实际问题的能力.

（2）植树问题教材简介.

例1：“同学们在全长100m 的小路一边植树，每隔5m 栽一棵（两端要栽）.一共可以栽多少棵树？”通过学生熟悉的植树情境，引导学生借助线段图，经历猜想、实验、抽象等数学活动过程，探索间隔与点之间的数量关系，建立植树问题的数学模型，再运用模型解决实际问题.让学生经历分析、思考、解决问题的全过程.

例2：“大象馆和猴山相距60m.绿化队要在两馆间的小路旁栽树（两端不栽），相邻两棵树之间的距离是3m.一共要栽多少棵树？”讨论两端都不栽的问题，通过迁移呈现出两端都不栽的线段图解决.

例3：“张伯伯准备在圆形池塘周围栽树.池塘的周长是120m，如果每隔10 m 栽一棵，一共要栽多少棵树？”讨论的是在封闭图形周围栽树的情形.教材首先提示研究方法：“先画图试试看.假设周长是40 m……”，当学生直观看出能栽4 棵后，教材并不急于让学生探索出封闭图形植树问题中的规律（即间隔数等于棵数），而是进一步提出问题：“如果把圆拉直成线段，你能发现什么？”从而把学生的思维引向深处，化曲为直后，封闭图形上植树其实可以转化成“一端栽另一端不栽”的情形.接下来，教材通过两位学生的对话“我发现间隔数与树一一对应”“相当于一端栽，一端不栽”，不仅揭示了封闭图形上植树的规律，更是为学生找到例3 与前面的例1、例2 间的联系.

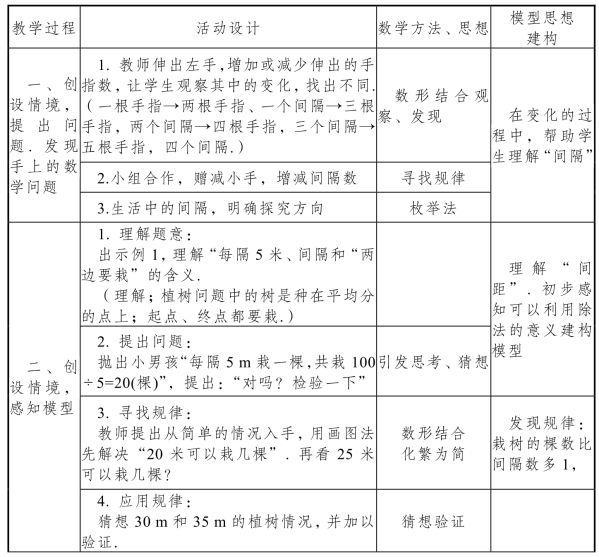
（3）植树问题（两端要栽）的模型思想的构建（见表9.1.2）.

表9.1.2　植树问题模型思想构建

续表

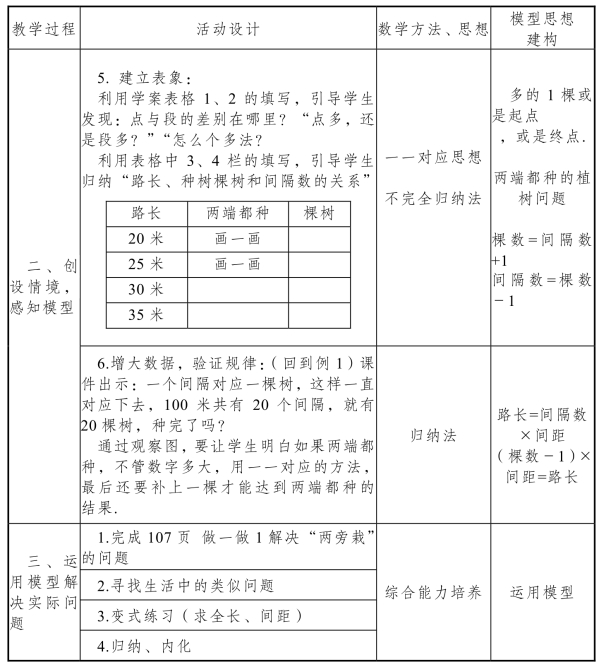
教材从具体到抽象，从特殊到一般，呈现分析、思考、解决问题的全过程.教材先由一个男孩说出容易出错的想法“每隔 5m 栽一棵，共栽100÷5=20(棵)”，接着由“对吗?检验一下”引出解决问题常用的方法—从简单的情况入手，渗透简单的化归思想后，呈现同学们用示意图和线段图分析问题的过程.通过画图先解决20m 和25m 的植树情况，并从中发现它们共同的规律：栽树的棵数比间隔数多1，接下来应用所发现的规律猜想30m 和35m 的植树问题，并加以验证.最后，引导学生概括出一条线段两端栽树的植树问题的一般规律，构建出“棵数=间隔数+1”的解题模型，并据此模型解决数据更大的问题.

由于有了前面的探索经验，在学习例2 时，学生自然会想到借助线段图来分析，所以教材呈现了3 位同学的分析和思考过程，引导学生继续画线段图进行分析，从而发现当两端都不栽树时，植树的棵数比间隔数少1，不难得出“棵数=间隔数－1”的解题模型.然后利用发现的规律解决相关的问题.

在例1、例2 的基础上，再让学生学习例3，通过“假设周长是40m，先画图试试看”引导学生从简单的情况入手进行探究.接着，通过问题“如果把圆拉直成线段，你能发现什么”，启发学生联系已有的知识找出这种植树问题的规律，即“栽树的棵数=间隔数”，并渗透转化为数学思想.

笔者认为：在“植树问题”中涉及“两端都种”“只种一端”与“两端都不种”这三种模型，在教学中应该以“两端都种”为基本模型，重点教学“两端都种”，不用对三种模型平均用力，在此基础上通过变式发展得到“只种一端”与“两端都不种”的数学模型.这样既把握了三种数学模型的内在联系，又避免了教学时间不足的矛盾.

2.关于鸽巢问题──“抽屉原理”

在数学问题中，有一类与“存在性”有关的问题，如任意367 名学生中，一定存在两名学生，他们在同一天过生日，13 个同学中一定存在两个同学的属相相同.在这类问题中，只需要确定某个物体（或某个人）的存在就可以了，并不需要指出是哪个物体（或哪个人），也不需要说明通过什么方式把这个存在的物体（或人）找出来.这类问题依据的理论，我们称之为“抽屉原理”.“抽屉原理”又称“鸽笼原理”，最先是由19 世纪的德国数学家狄里克雷提出来的，所以又称“狄里克雷原理”.

“抽屉原理”──鸽巢问题是人教版《义务教育课程标准实验教科书数学》（2013 版）六年级下册168～71 页数学广角中的教学内容，它包含了数学中的模型思想以及假设、枚举、反证、归纳等思想方法.该部分教材借助例1“把4 支铅笔放进3 个文具盒中”的操作情境，介绍了一类较简单的“抽屉原理”，即把n+1 个物体任意分放进n 个空抽屉里（m＞n，n 是非0 自然数），那么一定有一个抽屉中放进了至少2 个物体.关于这类问题，学生在现实生活中已积累了一定的感性经验.教学时可以充分利用学生的生活经验，放手让学生自主思考，先采用自己的方法进行“证明”，然后再进行交流，在交流中引导学生对“枚举法”“反证法”“假设法”等方法进行比较，使学生逐步学会运用一般性的数学方法来思考问题，发展学生的抽象思维能力.学生通过本内容的学习，学会利用“抽屉问题”解决简单的实际问题.在此过程中，让学生初步经历“数学证明”的过程.实际上，通过“说理”的方式来理解“抽屉原理”的过程就是一种数学证明的雏形，有助于提高学生的逻辑思维能力，为以后学习较严密的数学证明做准备.同时，在教学中注意培养学生的“抽屉原理”的“模型”思想，将具体问题数学化、模型化.

（1）抽屉原理的教学目标.(www.xing528.com)

① 经历“抽屉原理”的探究过程，初步了解“抽屉原理”，会用“抽屉原理”解决简单的实际问题.

② 通过“抽屉原理”的学习，增强对逻辑推理、模型思想的体验，提高学习数学的兴趣和应用能力.

（2）抽屉原理的教材简介.

例1：“4 支铅笔放入3 个文具盒，怎么放？有几种不同的放法？”描述“抽屉原理”的最简单的情况.教材呈现了两种思考方法：第一种方法是用操作的方法，罗列所有的方法，通过归纳看到在这四种情况都是满足结论的；还可以是说理的方式，先在每个笔筒里放1 支，这时剩下1 支，剩下的1 支不管放入哪一个笔筒中，这时都会有一个笔筒里有2 支铅笔.通过本例的教学，使学生感知这类问题的基本结构，掌握两种思考的方法──枚举和假设，理解问题中关键词语“总有”和“至少”的含义，形成对“抽屉原理”的初步认识.

例2：“5 本书放入2 个抽屉，看看有几种方法？通过观察，你发现了什么？”描述“抽屉原理”更为一般的形式，即“把多个（是正整数）物体任意分放进n 个空抽屉里，那么一定有一个抽屉中放进了至少n+1 个物体”.教材探究把7 本书放进3 个抽屉里，总有一个抽屉里至少放进3 本书的情形.

例3：“摸球问题”是抽屉原理的一个逆向应用.要解决这个问题，可以把两种“颜色”看成两个“抽屉”，“同色”就意味着“同一个抽屉”.这样，就可以把“摸球问题”转化为“抽屉问题”.教材指出学生可以通过先猜测再验证的方法来解决问题，再给予提示.

（3）抽屉原理的模型思想构建.

例1 描述的是最简单的“抽屉原理”：“4 支铅笔放入3 个文具盒，怎么放？有几种不同的放法？”.教材呈现了两种思考方法.第一种方法是用操作的方法进行枚举.通过直观地摆铅笔，发现把4 支铅笔分配到3 个文具盒中一共有四种情况（数的分解），即（4，0，0），（3，1，0），（2，2，0），（2，1，1）.每一种结果的三个数中，至少有一个数是不小于2 的.

第二种方法采用的是“反证法”或“假设法”的思路，即假设先在每个文具盒中放1 支铅笔，3 个文具盒里就放了3 支铅笔.还剩下1 支，放入任意一个文具盒，那么这个文具盒中就有2 支铅笔了.这种方法比第一种方法更为抽象，更具一般性.

在解决了“4 支铅笔放进3 个文具盒”的问题以后，可让学生思考：

① 把5 支铅笔放进4 个文具盒，结果是否一样呢？

② 把6 支铅笔放进5 个文具盒呢？

③ 把100 支铅笔放进99 个文具盒呢？

引导学生得出一般性的结论：只要放的铅笔数比文具盒的数量多1，总有一个文具盒里至少放进2 支铅笔.

接着，可以继续提问：如果要放的铅笔数比文具盒的数量多2，多3，多4 呢？引导学生发现：把 m 个物体任意放进n 个空抽屉里（m＞n，n是非0 自然数），那么一定有一个抽屉中放进了至少2 个物体.

例2 描述了“抽屉原理”更为一般的形式：“5 本书放入2 个抽屉，看看有几种方法？通过观察，你发现了什么？”

学生仍然可以采用枚举的方法，把5 分解成两个数，有（5，0），（4，1），（3，2）三种情况.在任何一种结果中，总有一个数不小于3.

更具一般性的仍然是假设的方法，即先把5 本书“平均分成2 份”.利用有余数除法5÷2=2……1 可以发现，“物体数÷抽屉数=商数……余数”，如果每个抽屉放进2 本，还剩1 本.把剩下的这1 本放进任何一个抽屉，该抽屉里就有3 本书了.初步感知“至少数=“商数+1”的解题模型.

学生研究了“把5 本书放进2 个抽屉”的问题后，进一步提出“如果一共有7 本书、9 本书，情况会怎样？”的问题，让学生利用前面的模型进行类推，得出“7 本书放进2 个抽屉，总有一个抽屉至少放进4 本书，9本书放进2 个抽屉，总有一个抽屉至少放进5 本书”的结论.

接着教师指出：像例1“4 支铅笔放入3 个文具盒，一定存在总有一个文具盒里至少放进2 支铅笔”，例2“5 本书放入2 个抽屉，总有一个抽屉不少于3 本书”的存在问题，在这类问题中，只需要确定某个物体（或某个人）的存在就可以了，并不需要指出是哪个物体（或哪个人），也不需要说明通过什么方式把这个存在的物体（或人）找出来.解决这类问题依据的理论，我们称之为“抽屉原理”.（这一点非常重要）

后面的例3 是“抽屉原理”的具体应用，也是运用“抽屉原理”进行逆向思维的一个典型例子.教学时，先引导学生思考本例的问题与前面所讲的抽屉原理是否有联系，有什么样的联系，引导学生把具体问题转化为“抽屉问题”，找出这里的“抽屉”是什么，“抽屉”有几个，再应用前面所学的“抽屉原理”进行反向推理.例如，在本例中，根据例1 中的结论“只要分的物体个数比抽屉数多，就能保证一定有一个抽屉至少有2 个球”就能推断“要保证有一个抽屉至少有2 个球，分的物体个数至少比抽屉数多1”.现在，“抽屉数”就是“颜色数”，结论就变成了：“要保证摸出两个同色的球，摸出的球的数量至少要比颜色种数多1.”在教学中，在实际问题和“抽屉问题”之间架起一座桥梁并不是一件容易的事.如果学生在理解时存在比较大的困难，也可以引导他们这样思考：球的颜色一共有两种，如果只取两个球，会出现三种情况：两个红球、一个红球一个篮球、两个篮球.如果再取一个球，不管是红球还是篮球，都能保证三个球中一定有两个同色的.

（4）“抽屉原理”的教学建议.

① 应让学生初步经历“数学证明”的过程.在小学阶段，虽然并不需要学生对涉及“抽屉原理”的相关现象给出严格的、形式化的证明，但仍可引导学生用直观的方式对某一具体现象进行“就事论事”式的解释，可以鼓励学生借助学具、实物操作或画草图的方式进行“说理”.

② 应有意识地培养学生的“模型”思想.教学时，要引导学生先判断某个问题是否属于用“抽屉原理”可以解决的范畴，如果可以，再思考如何寻找隐藏在其背后的“抽屉问题”的一般模型.这个过程实际上是学生经历将具体问题“数学化”的过程.

③ 要适当把握教学要求.“抽屉原理”的应用广泛且灵活多变，因此，用“抽屉原理”来解决实际问题时，经常会遇到一些困难.例如，有时要找到实际问题与“抽屉问题”之间的联系并不容易，即使找到了，也很难确定用什么作为“抽屉”，要用几个“抽屉”.因此，教学时，不必过于追求学生“说理”的严密性，只要能结合具体问题把大致意思说出来就可以了，更要允许学生借助实物操作等直观方式进行猜测、验证.