基于多智能体遗传算法的建模方法与技术

1.基于多智能体遗传算法的建模方法原理

针对超高维函数优化问题，人们提出了将智能体对环境的感知和反作用能力与遗传算法的搜索方法相结合的计算智能建模方法，即所谓的多智能体遗传算法。其方法原理十分清晰，首先由若干个智能体相互作用或协同工作构成多智能体计算系统，再根据解决问题的含义与目的、生存环境、局部环境和可采取的行为等方面的内容来设计用于函数优化的智能体。

函数优化问题的数学模型为

式中，f（X）为目标函数；S是边界为（i=1，2，…，n）的n维搜索空间，S⊆Rn，即S。

用于函数优化的智能体定义如下。

定义1　一个智能体a表示待优化函数的一个候选解，它的能量等于其目标函数值的相反数，即

智能体的目的是尽可能地增大其能量。由此可见，每个智能体都具有待优化函数的所有变量。

为了实现智能体的局部感知能力，生存环境被组织成网格结构，如图7.26所示，并有如下定义。

图7.26　智能体网格

定义2　所有智能体均生存在一个网络环境中，称为智能体网格，记为L。网格大小为Lsize×Lsize。其中，Lsize为整数。每个智能体固定在一个格点上，即处于第i行、第j列的智能体为Li，j（i，j=1，2，…，Lsize），则智能体Li，j的邻域为

式中

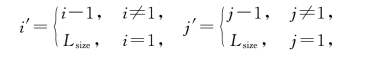
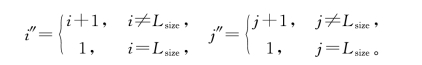
每个智能体不能移动，只能与其邻域发生相互作用。

应当指出，在智能体网格中，每个圆圈表示一个智能体，其中的数字为该智能体在网格中的位置，有连线的两个智能体方可发生相互作用。为了达到目的，每个智能体都可以采取一些行为与其邻域间的其他智能体展开竞争或合作，以便获得更多资源并增加自身能量，且在发生作用后，将其信息传给它们，于是信息便渐渐扩放到整个智能体网格，由此可见，智能体网格模型更接近于自然进化机制。

在上述思想基础上，我们可设计出4个智能体遗传算子，即邻域竞争算子、邻域正交叉算子、变异算子和自学习算子，其中，前两者分别实现智能体的竞争和合作，而后两者用以实现智能体利用自身知识的行为，并由此可得到多智能体遗传算法（MAGA）。对于这种算法，实验表明，即使对高达10 000维的函数，多智能体遗传算法也能实现快速精确的求解。

2.技术特点

（1）智能体是一个物理的或抽象的实体，它能作用于自身和环境，并对环境做出反应。它所具有的局部感知、竞争协作，以及自学习能力为求解复杂问题，特别是高维大规模的复杂系统建模提供了极好的条件和基础。(www.xing528.com)

（2）多智能体遗传算法将多智能体系统与传统遗传算法相结合，通过设计新的算子来实现智能体行为，以形成新的面向智能体的交叉、变异等操作，从而达到提高算法性能的目的。

（3）多智能体算法是在已有进化算法模型的基础上，通过引入智能体与环境，以及智能体间相互作用来实现全局优化的先进算法，该算法有对高维函数快速精确优化的突出特点，即以更低的计算量来获得更高质量的问题解。

3.典型应用

例1　利用MAGA求解10 000维函数f1～f10的性能.

设Lt表示第t代的智能体网格，和是Lt和Lt+1间的中间代智能体网格；Bestt是L0，L1，…，Lt中最优的智能体，CBestt是Lt中最优的智能体，Pc和Pm是预先设定的参数，分别控制邻域正交交叉算子和变异算子操作。在此条件下，有多智能体遗传算法如下：

①初始化L0，更新Best0，令t→0；

②对Lt中的每个智能体执行邻域竞争算子，得；

③对中的每个智能体，若U（0，1）＜Pc，则将邻域正交交叉算子作用在其上，得到；

④对中的每个智能体，若U（0，1）＜Pm，则将变异算子作用在其上，得到Lt+1；

⑤从Lt+1中找出CBestt+1，并将自学习算子作用其上；

⑥如果Energy（CBestt+1）＞Energy（CBestt），则令Bestt+1←CBestt+1，否则令Bestt+1←Bestt，CBestt+1←Bestt；

⑦如果终止条件满足，输出Bestt并停止，否则，令t←t+1并转步骤②。

在此，MAGA的终止条件为满足式（7.4.19）：

式中，fmin为最优解；fbest为算法的当前代所求的解。

为了保持一致，对所有函数均取ε=10-4。

为了进行比较，可同时利用上述MAGA及AEA（自适应演化算法）求解万维函数优化问题。表7.2给出了步长为500时，随机50次实验，AEA和MAGA对万维函数f1～f10的平均函数评价次数和O（na）的逼近结果。

表7.2　AEA和MAGA优化万维函数的平均评价次数和O（na）逼近结果比较

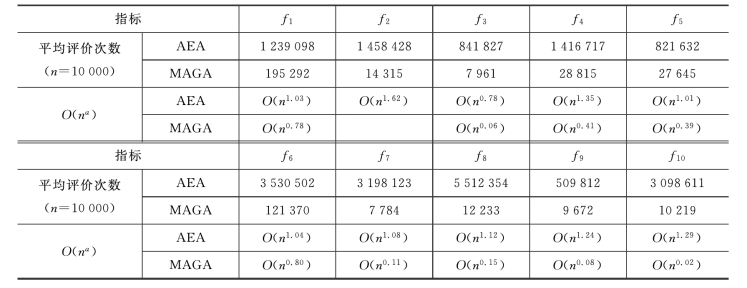
由此表可见，①AEA所用的评价次数远大于MAGA所用的评价次数；②10个函数中有9个AEA的复杂度都差于O（n），只有f3是O（n0.78），而MAGA对这10个函数的复杂度均较低，除f2外，均优于O（n）.

综上所述，MAGA的复杂度非常低，性能相当优越，具有很好的优化高维函数的能力。