基于模糊认知图的复杂系统虚拟实现方法及应用

1.模糊认知图与模糊虚拟世界

虚拟世界是指一个在“虚拟现实”或“电脑空间”中变化的世界。一个虚拟世界用一个似真非真的因果媒介将人类与计算机联系起来，使人类获得似真非真的现实世界。从广义上讲，一个虚拟世界就是一个动力系统。当参与者在虚拟世界中移动时，他们促使事件发生，添入新的因果模式，影响并响应旧模式。反过来，虚拟世界也作用于参与者，或作用于物理、社会环境。虚拟世界改变其行为，并可改变它自身的因果关系网。参与者与其虚拟世界之间的这种反馈因果性形成了一个复杂的动力系统，这个系统可以模拟事件、参与者、行为与数据，并且这些模拟对象随时间展开。

模糊认知图（fuzzy cognitive map，FCM）是具有反馈的模糊符号组合。FCM是一个模糊有向图，其结点代表以某种程度发生的模糊集合或事件。结点是因果概念，它们可以表示事件、行为、值、目标，以及分布参数等。有向边代表概念间的模糊规则或部分因果流。FCM能够在很大的模糊块内模拟虚拟世界，它们将因果网模拟为一个模糊有向图。在一个“捕食-被捕食”的世界中，生存威胁促使被捕食者逃走。当威胁的程度增大或减小时，逃走的程度相应地增大或减小。当一些其他的结点增大或减小时，模糊规则表明了某个结点增大或减小了多少。

FCM结点还可用来控制其自身的FCM，以生成一个虚拟世界分级系统中的嵌套FCM。FCM自身相当于一个非线性动力系统，它可以模拟结点输入与输出之间复杂的非线性关系，将输入映射为输出的平衡态。每个输入都在虚拟状态空间中开辟了一条通路。在简单的FCM中，通路终止于一个不动点或极限环。在复杂的FCM中，通路可能终止于一个非周期的吸引子或混沌吸引子。如图7.19所示为一个单位正方形中具有不动点、极限圈和混沌吸引子的FCM状态空间。该系统最多有4个模糊边规则，一个更复杂的FCM可能有3个模糊中间规则，其形式为“如果输入状态向量为C，则吸引子为A。”状态C0收敛于一个不动点F，其他的输入可能收敛于一个极限环或混沌吸引子。

图7.19　具有两个结点单位正方形的FCM状态间

（1）简单FCMs。简单的FCMs具有二值结点与三值边。概念值Ci在［0，1］中取值，因果边在［-1，0，1］中取值，因此，对于一个概念来说，每个简单FCM的状态向量都是模糊立方体ln中2n个顶点中的一个。轨道从一个顶点跳至另一个顶点。

（2）FCM检索。当FCM动力系统达到平衡时，FCM开始检索。简单的FCM推理为一个矩阵——向量乘积设置阈值。状态向量Cn在FCM的邻接矩阵E：C1→E→C2→E→C3…中循环。系统将加权输入非线性地变换为每个结点Ci

其中S（x）是一个有界信号函数。对于简单的FCM，Sigmoid函数

逼近一个二值阈函数，其中c＞0。

（3）增强的FCM。FCM矩阵进行可加性组合，以形成新的FCM，这使得在虚拟世界中可以组合不同参与者或不同环境的FCM。新的（增强的）FCM包括了对虚拟世界中所有参与者与环境的因果概念的联合。如果一个FCM不包含某个概念，则相应的行与列都为零。每个参与者的增强（用零填充）FCM矩阵之和组成了虚拟世界

其中，wi是第i个FCM Fi的正权重，权重代表了每个FCM在虚拟世界中的相对值，并可衡量FCM的任意子图的权重。

（4）嵌套的FCMs。当FCM定义了动力性物理与社会环境时，就为虚拟世界赋予了目标与意向。由此可生成一个虚拟世界所需的“一般表达”。FCM可以组合简单的行为以模拟复杂的“智力”行为。在一个嵌套FCM中，每个结点可依次控制其自身的简单的FCM。

FCM嵌套对输入而言是可多达任意数量的模糊集。一个概念可以分解为更小的模糊集或子概念。集合由边或规则连接起来，这就形成了每个结点的离散多值输出。对于形如式（7.4.2）的信号函数来说，足够多的结点可以使这种前馈系统逼近任意连续函数。子概念Qij划分了模糊概念Cj

FCM边或规则可将一个子概念映射到另一个子概念，这些子概念映射形成了一个将输入映射至输出的模糊系统或模糊“如果……则”规则的集合。每个映射都是一个连接模糊集的模糊规则或状态空间规则补块。在“输入-输出”状态空间中，补块覆盖了某个函数的图形。模糊系统将重叠的补块平均，以生成一个连续函数的逼近。图7.20表示在FCM中，子概念是如何映射至不同反应的。这就产生了一个对虚拟世界中的变化更多样的反应。

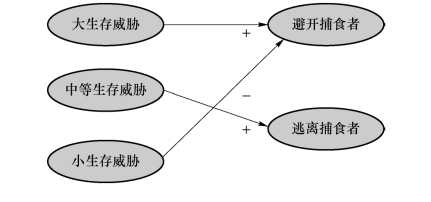
图7.20　子概念映射至其他概念产生的一个更多样的反应

2.虚拟海底世界

图7.21表示一只虚拟海豚的简单FCM，它给出了海豚生活中目的与行为的因果网。联系矩阵D用数字表示这些因果联系：第i行列出从因果概念Di引出的边eik的联系强度。第i列列出到达概念Di的边eki的联系强度。

图7.21　模糊虚拟世界对一只海豚的控制的三值模糊认知图

（1）增强的虚拟世界。图7.22表示了一个海底虚拟世界的增强FCM。它通过式（7.4.3）将鱼群、鲨鱼、海豚群组合为FCM：F=F鱼+F鲨+F海豚。这些FCM之间的新的联系是那些以大吃小的捕食者与被捕食者，参与者追逐、逃跑，一个吃掉另一个。一条饥饿的鲨鱼追逐海豚，这就导致了极限环（C1，C2，C3，C3）。由于参与者对对方的反应只有很少的几种方式，所以增强的FCM矩阵生成了一个大而稀的FCM。

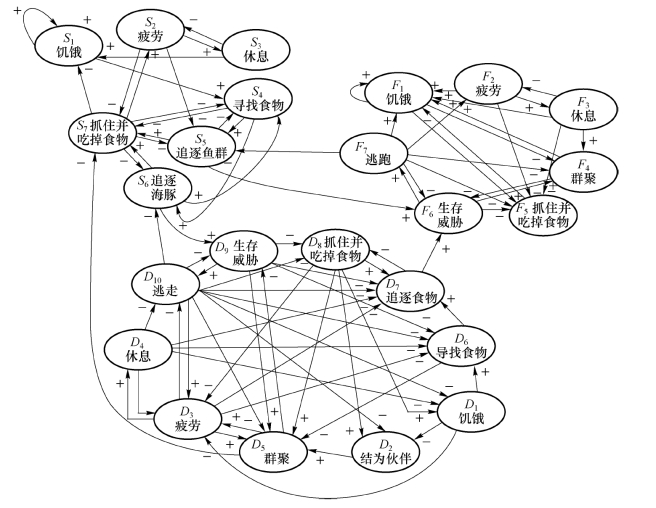
图7.22　一个海底虚拟世界增强的FCM

增强的FCM是虚拟世界中移动参与者，也就是说，这种FCM的二值输出状态移动了参与者，每个FCM状态映射为移动的方程或逼近函数。

下面是一个简单的正迭代方程

其中速度v（t）在时间段Δt中不改变，FCM得到了移动的方向与量值。速度的量值依赖于FCM状态，如果FCM状态为“跑开”，则速度为“快”；如果FCM状态是“休息”，则速度为“慢”。被捕食者选择能以最大限度远离捕食者的方向。捕食者追逐被捕食者，当一个捕食者寻找食物时，他随机地游动，每个状态都使参与者在海中移动。

（2）对鱼群的嵌套FCM。在一个简单的FCM中，将鱼群对威胁的反应与“若有生存威胁，则逃跑”的规则连接起来。这个规则没有模拟不同威胁的影响，要想模拟这样的影响，必须有一个嵌套的FCM：“若有小的生存威胁，则避开捕食者”或“若有大的生存威胁，则逃离捕食者”。这样就将一个生存威胁的概念分为两个子概念，每个子概念映射为一个不同的生存对策。

当威胁程度改变时，鱼的行为也随之改变，威胁的大小是捕食者的大小、速度与袭击角度的函数。一个小威胁导致躲避行为，图7.23（a）描绘了鱼怎样避开捕食者，鱼以角度α移动，使得它与捕食者之间的距离最远，

其中Vp与Vf分别为捕食者与鱼的速度；αm是根据捕食者的视角γp使时间最小化的角，3者满足：

大的生存威胁使鱼逃离捕食者。鱼试图使它与捕食者之间的最短距离Dp最大(www.xing528.com)

其中X0是捕食者与被捕食者之间的初始距离，α是被捕食者的逃离角度，Vp与Vf分别为

捕食者与鱼的速度。如图7.23（b）所示为鱼是怎样逃离捕食者的。解是一个速度比

当每条鱼都试图增加其生存机会时，这些威胁反应就在鱼群中引起“喷泉效果”和“爆炸效果”。当一个捕食者向一个鱼群移动产生喷泉效果时，鱼群分散开，并在捕食者周围游动，在捕食者身后又重聚成一群。在爆炸效果中，鱼群以球形散开，逃离捕食者。

3.自适应模糊认知图

一个自适应FCM的因果网随时间而改变。因果网从数据中学习，其结果是使因果边或规则的符号与量值发生变化。式（7.4.3）的可加性体系是一种因果学习，因为它改变了FCM边的强度，一般地，一条边e会随某条一级学习规则的变化而变化。

其中gij是一个强追函数。当数据激活概念结点不久后，就在边中产生了因果模式。因果学习在fij中是局部的，它只依赖于自身的值和连续的结点信号

图7.23　当威胁程度改变时，鱼群改变其行为

当威胁程度改变时，鱼群改变其行为。（a）鱼群在捕食者的视角内使时间最小化。角度αm代表当鱼游动速度很快时的逃离角度，角度γp代表当捕食者游动速度很快时期望速度的方向。（b）鱼将其自身与捕食者之间的距离最大化，以逃离捕食者。当鱼游动的速度大于捕食者时，鱼径直向前游，如果捕食者游得更快，鱼则以某个角度游开。

联想学习或Hebb（一种无监督学习规则）学习可将FCM或时间联想记忆（TAM）中的一些极限环进行编码，在（7.4.10）中加入成对的相关矩阵，这种方法只能存储很少的一部分模式。微分Hebb学习将（7.4.11）中一个概念的变化进行编码。这两种学习都是局部的，计算量也很小。

为了将联系矩阵E中的二值极限环进行编码，TAM的方法是将连续状态中的加权相关阵相加，为了将极限环C1→C2→C3→C1进行编码，首先要将每个0用-1来代替，从而将每个二值状态Ci转化为一个二极状态矢量Xi，此时E即为加权和

极限环的长度应小于概念的数量，否则就会发生干扰。每个相关阵对的适当权重可以改变编码，并可增强FCM的存储量。联想学习是神经元网络中的一类无监督学习，Hebb学习规则为

虚拟世界可通过（7.4.12）或（7.4.13）为一个事件序列进行编码，一个简单的追捕循环为C1→C2→C3→C1…

微分Hebb学习规则与概念变化或速度相关，即

因此，当且仅当概念Ci与Cj向同一方向移动时，；当且仅当Ci与Cj朝相反的方向运动时，（xi）（xj）＜0。在此意义上，式（7.4.14）学习了因果变化的模式。式（7.4.14）的一级结构意味着eij（t）是成对（或滞后）变化的指数型加权平均，最近的变化具有最大的权重。离散的变化ΔCi（t）=Ci（t）-Ci（t-1）取值于［-1，0，1］，离散微分Hebb学习的形式可为

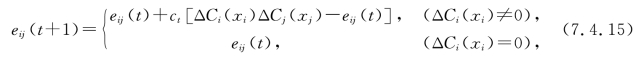
其中ct是随时间递减的学习系数。如果概念Ci与Cj沿同一方向移动，则ΔCiΔCj＞0；如果二者沿相反方向移动，则ΔCiΔCj＜0。仅当一个概念变化时，E发生变化。改变后的边渐渐“遗忘”旧的因果变化，而“记住”新的变化。如果这种因果规则在多倍因果变化与效果变化之间建立起关系式，那么它就可以学习高级的因果关系。

使用微分Hebb学习来将FCM中捕食序列与追逐序列进行编码，仅当其等于1或-1时，第i行中的概念开始学习。图7.24（a）给出了来自人工设计的极限环，图7.24（b）给出了通过微分Hebb学习找到的FCM的极限环，DHL极限环只是较短的一步。两个FCM在210二值状态矢量空间中均仅有一个极限环和一个零不动点。E0的值在两个区间之上不发生变化。式（7.4.15）中的学习规则仅当结点中有变化时，才开始学习。

图7.24　手工设计的系统与通过微分Hebb学习找到的FCM之间的极限环比较

注：每一列都是一个二值状态空间

4.基于模糊认知图的虚拟海底世界

模糊认知图可以模拟一个虚拟世界的因果网，FCM可控制其局部与全局的非线性行为、相连的局部因果规则或边，以及模糊概念模拟了事件内部或事件之间的因果连接。全局的FCM非线性动力赋予了虚拟世界一个“时间的方向”。使用者可根据意愿改变这些动力性，继而改变虚拟世界中的因果过程。FCM允许专家与用户画出因果图，而不是列出方程来选择一个因果网。

FCM还有助于使数据可视化，它表明了在因果网中变量之间如何彼此联系。由FCM输出状态可以画出一张虚拟世界的卡通画，如图7.25所示。这张卡通画给出了海豚追逐、休息、捕食的过程，当系统轨道在FCM状态空间中移动时，该图激活了FCM的动力性。这一点可以应用于经济、医学、历史及政治的模型中，其中联系与因果网能够以复杂的方式改变，这种方式产生于对一个FCM因果或规则的符号与量值的改变。

图7.25　基于FCM输出状态的虚拟海底世界的卡通图

组合FCM的可加性结构允许我们使用Delphi预测法或问卷调查法来获取知识，这些新的因果网能够改变一个将其因果网作为类神经元学习规则过程的时间序列数据来学习的自适应FCM。专家们可将其FCM矩阵与自适应FCM相加，进行初始化或指导学习，这样一个因果网可以学习用户的值与行为习惯，甚至还可以对其进行测试并训练它们。

更复杂的FCM有更复杂的动力性，能模拟更复杂的虚拟世界。每个概念结点都能够以其自身的时间尺度与非线性方式激活，因果流动边或规则也有其自身的时间尺度，可能会以非线性方式增大或减小通过它们的因果流。在具有阈概念与常值边权重的简单FCM中，这种行为是不适合的。我们还可以在=F（x）中寻找一个FCM逼近函数F，至少能逼近一个模糊空间中的任意动力系统=F（x）的定性吸引子结构。

如果一个FCM能够用更多的非线性数学方法来改变其结点与边，它就可以模拟这些复杂的虚拟世界，所付出的代价是，虚拟世界可能会成为具有未知平衡行为的混沌虚拟世界。一些用户可能想把这些新颖的结果加入虚拟世界，以使其更有吸引力。用户也许会选择一个虚拟世界，它是适度非线性的，并有周期平衡态，而另一个极端则是用户选择的虚拟世界具有强烈的非线性且只有非周期的平衡态，可供说明的例子为重力势能可随机地按人们意愿发生变化的虚拟网球比赛。

对一个虚拟世界来说，模糊性与非线性都是设计的参数，它们可以产生一个较好现实模型，否则它们就没有实际意义。