基于GMDH建模的典型应用：详解和案例研究

例8　GMDH在我国降雨量预测中的应用。

吴耿锋、彭虎等学者提出了应用GMDH预测我国降雨量的方法，并研制出基于GMDH的混沌时间序列建模方法。

该方法的核心是将降雨量的混沌参数提取后体现在GMDH网络结构中，并通过这样的GMDH模型对降雨量进行预测。

预测来自对已往数据轨迹的把握，而任何一种轨迹都可以由如下多项式来表示：

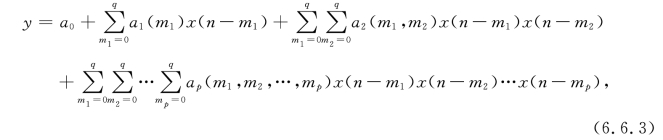
式中，a0，a1（·），…，ap（·）是系数；m1，m2，…，mp是变量的阶数；x（·）是自变量；y（·）是因变量。

显然，只要有足够数据和计算量我们就可以通过拟合方法来得到轨迹表达式，但是对于降雨量预测这样的超高维系统，用直接拟合式（6.6.3）来建立模型，需要大量的拟合数据和运算量，故很难实施。GMDH可将单一多项式的拟合分解为数个拟合单元，并以网状递进的方式排列和连接这些单元，从而构成GMDH网络结构，来完成对复杂系统的建模。与一般神经网络相比，GMDH更贴近于人的运行机制，且建模中采用AC准则，逐层剔除多项式的弱贡献项，用较少的数据就能达到成功建模的目的。图6.16（a）、（b）分别给出了典型的GMDH网络结构及其基本处理单元的示意图。

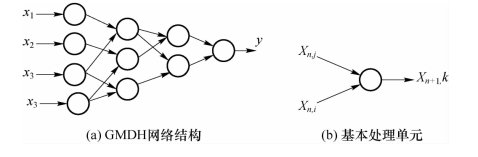
图6.16　GMDH网络结构及其基本处理单元示意图

这是一种双输入单输出的结构，其输入与输出的关系为

利用该GMDH网络的建模步骤如下。

（1）提取基本单元。在总数为n的数据样本中取出n1个样本作为训练样本或建模样本（一般取n1=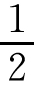n），从这些样本的m个变量中任取两个xi，xj（i，j=1，2，…，m，i≠j），以Y为输出，用最小二乘法建立如式（6.6.4）的处理单元，于是可得到个基本单元。

（2）建立输入层。先设定一个阈值Eg（在此将Eg设为当前所有单元输出方差的均值），将其余样本n2作为校核样本，将n2中对应于建模样本n1的相应变量值分别代入上述处理单元，算出处理单元的输出与实际输出的方差E，再把各单元的方差与Eg比较，保留那些低于阈值的单元（设共有u1个单元），记录这些单元中的最小方差。这样，便得到了输入层的单元。

（3）构建中间层。将全部数据中的相应变量代入输入层单元进行计算，得到输入层的输出Y（1）（u）（u=1，2，…，u1）。将Y（1）（u）当作第2层的输入，重复上述两步，可得到第2层处理单元u2个，第2层的输出Y（2）（u）（u=1，2，…，u2），以及第2层的最小方差。若，则第2层构建成功，便可按同样方法继续构建下一层。

（4）建立输出层。假设进行到第k+1层，发现该层的最小方差，则终止建模，并将第k层中方差最小的那个单元作为输出单元。最后，将与输出单元相关的上层单元逐层连接。至此，便得到以样本为基础的GMDH网络模型。

（5）构造具有混沌特征的GMDH网络。降雨量的变化是多种相互影响的自然因素策动的结果，其中某些因素成因不明、变化复杂，致使降雨量数据表现出不定性和混沌特征。故需要构造具有混沌特征的GMDH网络，以便对数据进行拟合。

首先可根据Grassberger-Procaccia分析法计算出关联维d，进而计算得到嵌入维

(www.xing528.com)

于是，相空间重构可以表示为

式中，τ表示延迟时间。

原时间序列x（n）（n=1，2，…，N）可表示为

式中，m=N-Mτ，一般取τ=1。这样，便形成了具有下式结构的降雨量数据构成的空间变量：

于是，便可将这些空间变量输入GMDH网络进行建模，经过建模后的GMDH模型能够输入样本并进行降雨量预测。

下面是蚌埠地区降雨量的预测实例。

所用的数据样本是淮河流域28个不同站近42年所采集到的月平均降雨量，图6.17给出了该地区近42年的1月份降雨量。

选取图6.17中前32个点的降雨量进行建模，对最近的10个点的降雨量进行预测，并与原数据值进行比较，其结果如表6.2所示。

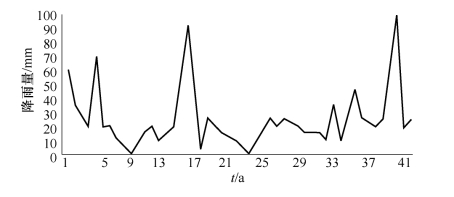
图6.17　蚌埠地区近42年的1月份降用量

表6.2　降雨量的预测值及相对误差

注：表中Es%=。

另外，这10个点的总体平均预测误差为

由此可见，基于GMDH的混沌时间序列建模方法用于降雨量预测的结果是令人满意的。