基于量子神经网络的建模方法与技术详解

基于量子神经网络建模是指在量子计算机或量子器的基础上构造复杂系统的神经网络模型。在这种建模方法中，引入量子理论，其目的在于充分利用量子计算超高速、超并行、指数级容量的特点，来改进传统神经网络的结构和性能，有关神经网络的原理我们在前面已经讲述，下面简单介绍量子计算。

在量子计算中，量子信息的基本单位是量子位，其取值除“0”或“1”外，还可以取“0”和“1”的任意线性叠加，如|Δ=a|0＞+b|+1＞，即量子位可处于叠加态。这里，a，b为复数，|a|2+|b|2=1，即|Δ＞是二维Hilbert空间的单向向量，｛|0＞|1＞｝称为量子系统的计算基态，可以表示为｛（1，0）T，（0，1）T｝。n个量子位的有序集合称为n位量子寄存器，n位量子寄存器的态|φ＞是n个量子位态|φi＞的张量级，|φn-1＞⊗|φn-2＞⊗…⊗||φ＞=|φn-1 φn-2…φ0＞φ0＞，它是N=2n维Hilbert空间的单位向量，有N个相正交的计算基态，可写成量子叠加态形式为，其中φi为复数，，|i＞|为其计算基态。在量子计算机中，处于叠加态的n位量子寄存器可以同时存储i=0，…，2n-1的所有N=2n个数，它们各以一定概率|φi|2同时存在。

由于量子并行，即作用于量子寄存器上的任意变换都是同时对所有N个数进行操作的，所以量子计算机的一次运算就可以产生2n个运算结果，这相当于常规计算机2n次操作或2n个处理器同时并行操作。由此可见，量子计算机的解题速度是任何常规计算机都达不到的。另外，量子计算机的功能之一是实现量子系统随时间的演化过程。量子计算过程实质上就是控制量子态，使其按算法要求的过程进行演化，这种演化可用算子作用于态矢来描述。为保证量子态的归一化，算子必定是幺正的，量子门则用于最基本的幺正操作。量子门组网络由多个量子门组成，它们的操作是同步的，可学习任意n维Hilbert空间的所有幺正变换，即量子门组网络在算法控制下可实现同常规计算一样的量子计算。

将上述量子计算同常规人工神经网络相结合，可产生不同结构的量子神经网络，具有代表性的量子神经网络有量子衍生神经网络、量子并行自组织网络、量子联想记忆网络、纠缠神经网络等。

2.基于量子神经网络的建模方法的技术特点

（1）基于量子神经网络的建模是一种崭新的技术，是量子计算与人工神经网络相结合的产物。

（2）基于量子神经网络的建模从结构和性能上大大改进了当前神经网络的不足，发挥了量子计算和神经网络的各自优势，是比常规神经网络更有效的复杂系统建模的重要新方法。

（3）量子神经网络作为一种混合的智能优化算法，可在传统计算机上实现。

3.基于量子神经网络的建模方法的典型应用

例7　对Kohonen自组织映射网络模型的改进。(www.xing528.com)

自组织特征映射模型于1981年由Kohonen教授提出，它包括自组织映射模型、自适应共振理论模型和对偶传播网等。其中，自组织映射模型（SOM）是一种基于生物神经细胞的神经网络，由处理单元阵列、比较选择机制、局部互连作用及自适应过程等4部分构成，其基本结构如图6.13所示。

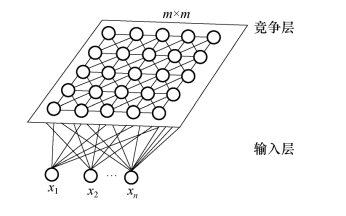
图6.13　SOM的基本结构

该模型的输入层与输出层神经元间为全互联方式。其整个算法分成两步，首先计算出输入样本矢量与各个输出点连接权的匹配值，从中找到最佳匹配输出点，然后对该结点及其相邻结点所对应的连接权矢量进行修正，使该结点的输入样本的匹配程度得以增强，而匹配程度可用式‖x-wi‖来计算，即

式中，x为输入样本矢量；y为最佳匹配结点；wi为修正结点i的权值；wj为最佳匹配结点的权值。

这种传统的Koronen SOM模型，仅是对生物脑认知机制的粗浅模拟，为了实现高性能，我们可利用量子理论对其改造，形成量子并行的SOM模型。该模型的输入、输出层均为神经元的二维阵列，一个输入层神经元只与一个而不是多个输出层神经元相连，神经元之间的每个连接被看作一个独立的处理器，输入、输出层神经元数及它们之间的连接数均等于输入信号个数（M）与数据可能的分类模板（P）的乘积（见图6.14）。由于该模型可同时进行M个SOM的训练，故适用于并行处理，且在训练过程中权值矩阵和距离矩阵的所有元素能同时进行计算，权值更新通过一系列同步运算完成，所以该过程与人脑的一次学习和记忆更为相似，又由于它采用了量子计算方法，从而大大降低了计算复杂度。例如，当M=1 000 000，P=100时，若采用传统算法实现并行SOM，则所需输入输出层神经元均为108个，可见运算量极大，且要把108个神经元放在同一层上几乎是不可能的。若采用量子计算，只需1og2108（约为27）个量子神经元，并且量子计算还具有并行计算的绝对优势。

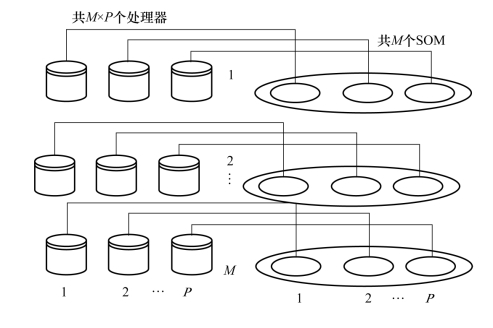
图6.14　量子并行SOM模型结构