大量的神经元通过突触连接成网络，其结构一般为层状和网状两大类。前向网络是典型的层状结构，如图6.11所示。它包含输入层、隐层（中间层）和输出层。输入，输出各为一层，而隐层可为多层。前向网络又称为前馈网络，因为这种网络采用误差反向传播学习算法，所以又称为BP（back propagation）网络。
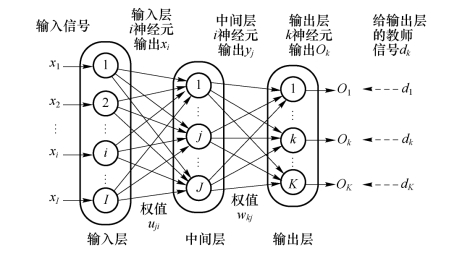
图6.11 前向网络的层状结构
1989年，罗伯特·赫克特·尼尔森（Robert Hecht-Nielson）证明了对于任何一个在闭区间内的连续函数都可以用一个隐层的BP网络来逼近，因而一个3层的BP网络可以完成任意的从n维到m维的映射。
BP网络的逼近过程是依靠学习算法来实现的。所谓神经网络的学习是指通过调整神经网络层之间神经元的连接强度（权重），从而影响该网络的输入输出关系，使该网络以一定精度完成任意的n维到m维的非线性映射，因此，我们可以利用BP网络对复杂系统进行辨识，从而建立复杂系统的输入输出模型（正模型或逆模型）。
如图6.12所示，是利用神经网络辨识复杂系统模型的原理示意图。图中的CS为待辨识的复杂系统，NN为神经网络，d为对系统的干扰。输入信号u（k）同时加到CS和NN上，测量出CS和NN的输出分别为y（k+1）和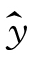
（k+1），利用二者之差即误差e（k+1）=y（k+1）-
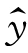（k+1），通过学习算法来修正NN的连接权值，以使e（k+1）→0，此时NN的辨识模型以足够的精度逼近复杂系统CS的模型。
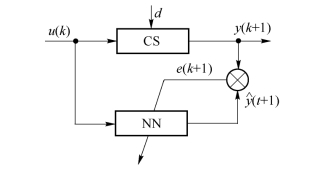
图6.12 神经网络辨识复杂系统模型
应该指出，用神经网络辨识得到的模型，是一个隐式模型，有关待辨识系统的输入输出关系的信息完全隐含在NN的权矩阵中，根据辨识要求的不同，NN系统辨识的结构也分多种形式。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
