最小二乘支持向量机软测量模型的构建

例3　4-CBA（对羧基苯甲醛）软测建模。

软测量技术是解决工业过程中普遍存在的难以在线测量变量估计问题的有效方法，它既可克服离线人工分析的时间滞后，又可以避免使用在线分析仪表所造成的费用昂贵，因而得到了广泛应用。4—CBA的软测量就是其中一例。

精对苯二甲酸（PTA）是生产聚酯的主要原料，由对二甲苯经液相催化氧化反应得到，其中4—CBA（对羧基苯甲醛）是主要的副产品，其含量大小直接影响PTA产品的质量（如着色）和能耗、酸耗等。为了保证PTA产品的纯度并节省能耗及酸耗，必须利用上述软测量技术对PTA生产过程中4—CBA的含量实施在线估计，因此，4—CBA软测量建模是必需的。该软测量建模选用基于主元分析（PCA）和最小二乘支持向量机方法，即首先运用PCA方法对初选的过程变量进行数据压缩和信息抽取，消除变量间的相关性，再通过最小二乘支持向量机对提取的PCA主成分进行训练，建立软测量模型，该方法的工作原理如图6.5所示。

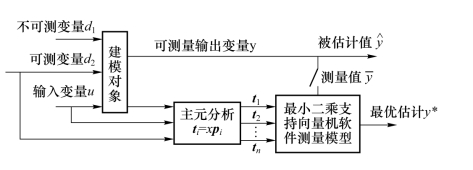
图6.5　基于PCA和最小二乘支持向量机的软测量原理框图

4-CBA软测量建模的具体过程如下。

（1）原始样本标准化。标准化处理的目的是消除量纲不同带来的不合理影响，处理后原始数据变换为均值为0，方差为1的标准数据集。

设Xn×m为原始样本数据矩阵，n为样本数，m为变量数，利用PCA可将该矩阵分解为下列形式：

式中，ti为主元，即得分向量，各得分向量之间是正交的；pi为负荷向量，各负荷向量亦是正交的，每个负荷向量的长都均为1，且数据X的变化主要体现在前k个负荷向量方向上；E为误差矩阵，忽略E往往会起到清除测量噪声的效果。

（2）计算主成分值。采用矩阵简化奇异值分解方法。

设标准化后的样本为

式中，Un×m、Vm×m为由奇异向量构成的两个正交矩阵；Σ为由奇异值构成的对角方阵，即Σ=diag（δ1，δ2，…，δn）。

计算每个主元的方差：

计算总的方差：

计算累积方差百分比：

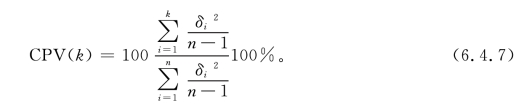
（3）找出所有累计方差百分比大于给定值（85%）的主元个数k，从而求出主元，通过主元分析可将n维输入变为k维主元变量。

（4）规定误差惩罚参数集和核参数集。这里，选用的核函数形式为高斯核函数

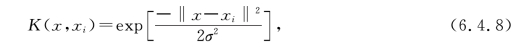
式中，；σ为核宽度。

（5）从上述两个参数集合中选取参数分别进行组合，并利用所选的参数，进行最小二乘支持向量机训练。

（6）利用测试集进行检验，返回步骤（5）直至检验结束。

（7）选出最佳参数组合，建立最小二乘支持向量机软测量模型，并用建立好的模型进行预测。为了建立最小二乘支持软测量模型，可在前述支持向量机的主要思想基础上，在优化中选择误差ξi的二次项，这时有

其中yi=ωTφ（xi）+b+ξi，i=1，2，…，l。

通过式（6.4.9）的对偶形式可求它的最优解。其对偶形式可以根据目标函数及约束条件建立Lagarangian函数

根据优化条件：(www.xing528.com)

可得：

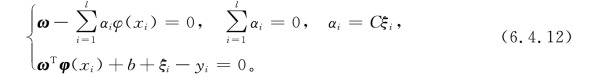
据此可将求解优化问题转化为求解线性方程：

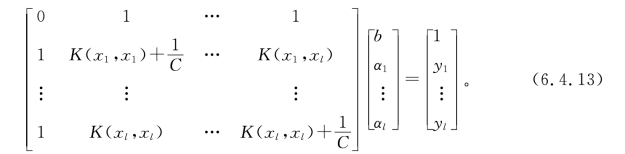
最后得最小二乘支持向量机的估计函数，即软测量模型为

在具体建立4-CBA软测量模型时，采用与4-CBA含量人工分析值对应时刻过程变量的小时平均值作为模型训练与测试的输入数据，共选取了380组有代表性的样本数据，并从中任意抽出180组数据作为学习样本来建立模型，其余200组作为测试样本来检验模型的泛化能力；按照积累方差配比大于85%选定了4个主元变量作为最小二乘支持向量机的输入变量；规定误差惩罚参数集SC=［100，80，50，40，10，5，0，0.5，0.25，0.1）和核参数集Sδ=｛5，3.1，0，0.7，0.5，0.2，0.1，0.05，0.025，0.01）。经训练后，最终选定正则化参数为50，核参数为0.2。图6.6（a）、（b）分别给出了训练样本集和测试样本集。由图可见，模型的估计值与人工分析值拟合得很好，其中训练均方根误差仅为0.0015。测试均方根误差为0.002 1。这说明此模型用于4-CBA含量变化软测量的精度较高，具有较强的泛化能力。

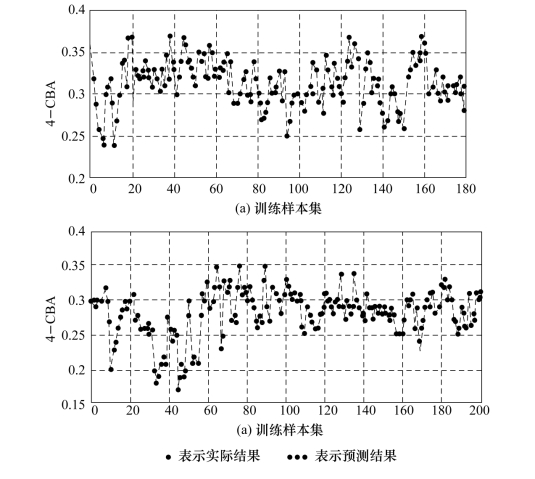
图6.6　4-CBA含量变化软测量估计值与实际值的拟合曲线

下面是支持向量机的几个典型应用简例

例4　手写阿拉伯数学识别问题。

该问题最先是为美国邮政系统自动分拣手写邮政编码的信函提出来的，作为支持向量机的第一个实际应用。目前已有两个标准数字数据库USPS和NIST被作为测试多种分类器优劣的标准。

USPS数据库包括7 291个训练样本点和2 007个测试样本点，每个样本点的输入均是手写阿拉伯数字和数学图像，其像素为16×16个，每个像素取0到255之间的灰度值。这样每个样本点的输入就可用16×16=256维的一个向量来表示，其中每个分量为灰度值。

NIST数据库包含6 000个训练样本点和10 000个测试样本点，每个样本点的输入含有20×20个像素。同样，每个样本点的输入就可用400维的向量来表示，其中每个分量也是在0到255之间的灰度值。

针对上述两个数据库，在利用支持向量机处理两类问题的基础上，可构造出解决多类问题的支持向量机，在这些支持向量机算法中，主要采用的是多项式核函数、径向基核函数及Sigmoid核函数。如USPS数据库就采用了多项式核函数

和径向核函数

例5　文本分类问题。

所谓文本分类是指根据文本内容进行自动归类。邮件过滤、网页搜索及办公自动化等领域都会遇到此类问题。Joachims和Dumais利用支持向量机对文本分类进行了深入研究，并获得了重要成果。被研究的第21 578号新闻数据库共有12 902个文本，其中9 603个为训练文本，3 299个为测试文本。每个文本约包含200个单词，分属于118类。在对数据库预处理去掉文本中与类别无关的单词后，数据库中共留9 947个词根，再按照词根顺序组成“字典”，最后把数据库中的每个文本根据该“字典”表示为9 947维向量X=［（x）1，…，（x）9947］T，其中

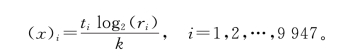
式中，ti表示文本中第i个词根出现的次数；ri为数据库中所有文本的个数（12 902个）与包含第i个词根的文本数之比；k为使‖x‖=1的尺寸。

选取的核函数为线性核函数

K（x，x'）=（x·x'）。

例6　生物信息学问题

在生物信息学中，有两个问题受到了人们的极大关注，其一是蛋白质问题；其二是基因问题。这两个问题都可以采用支持向量机来进行研究。

蛋白质被视为生物生存的最主要物质基础之一，蛋白质的分类是生物信息学研究的主要方面。研究表明，蛋白质可以看作一个以氨基酸为元素组成的序列，组成人体的氨基酸有20种：a1=A（丙氨酸），a2=R（精氨酸），…a20=V（缬氨酸），于是，每种蛋白质将对应一个从20种氨基酸种抽取而排列成一定长度的序列，如：

问题是如何由已知的某一蛋白质氨基酸序列式（6.4.17）来推断该蛋白质是否属于已有的各类蛋白质？或者如何确定它属于已有的哪一类蛋白质？显然，这是一个分类问题。我们可以把式（6.4.17）序列看作输入，把蛋白质类别作为输出，用已知的各类蛋白质构成训练集，通过支持向量分类机来研究这一问题。

人类的遗传功能是由核酸承担的，核酸分为脱氧核糖核酸（DNA）和核糖核酸（RNA）两大类，它们都由核苷酸构成。DNA分子上4种核苷酸的排列组合顺序蕴涵了丰富的遗传信息，其中每3个相邻的核苷酸含1个遗传密码。基因就是指染色体所运载的DNA双螺旋链上的一段序列，该序列由4种核苷酸通过不同的排列组合形成，是生物性状遗传的基本功能单位，因此，对基因的准确定位和全顺序分析是研究人类遗传及医疗的重要途径。显然，利用支持向量分类机，同样可以有效地研究上述基因问题。