分形理论：自相似性与分数维，探索英国海岸线长度之谜

1.什么是分形

我们知道，具有规则形状的物体，可以用欧几里得几何中的长度、面积、体积来表示，但是，自然界中还存在着大量形状不规则的物体。例如山脉、海岸、河流、雪花、浮云、树林、人体等，都是不规则的形体。研究自然界中非规则对象的几何学叫分形。

分形的基本性质是自相似性。若一个物体的一部分放大后看起来仍与整个物体一样，那么这个物体就是自相似的。自然界中存在着许多具有自相似特征的现象。例如，在股票市场的道·琼斯指数中，某一阶段的曲线图总和另一更长的阶段的曲线图极为相似。海岸线虽然很复杂，却有一个重要性质——自相似性。从不同比例尺的地图上，我们可以看到海岸线的形状大体相同，其曲折、复杂程度是相似的。换言之，海岸线的任何一小部分都包含与整体相同的或相似的细节。其实，远不止这些，例如，同一个水系上的主流分布着许多支流，在支流上又分布着许多小支流……主流和支流的分布情况几乎相同，即它们具有自相似的层次。在地学中，山中有山，景中有景，这些景物往往具有嵌套的自相似结构。在大气系统中，大漩涡中有小漩涡，小漩涡中有更小的漩涡，它们也具有自相似的结构。总之，自然界是以自相似的形式存在和演化的。

为了研究具有自相似结构的几何物体，1986年，法国数学家曼德布罗特（Benoit Mandebrot）提出了分形的概念并给出了分形的定义：组成部分以某种方式与整体相似的形体叫分形。

分形理论（fractral theory）问世的时间虽然不长，但由于分形几何不同于欧几里得几何，它擅长描述自然界中普遍存在的非规则事物，对人们探索事物局部与整体的关系、复杂系统的层次性、自相似结构等提供了新的概念和方法，无论是在自然科学领域还是社会科学领域，分形方法都具有广阔的应用前景。

2.分形的主要特征

（1）自相似性

目前严格地定义分形是一件非常复杂且十分困难的事情。最为流行的一个定义是：分形是一种具有自相似特性的现象、图像或物理过程。在分形中，每一组成在特征上都和整体相似。也就是说，自相似实际上是子系统和系统相似。从哲学上看是部分同整体的关系。自相似现象普遍存在于自然界中。例如，自相似生物系统、自相似人体系统、自相似天体系统、自相似地质系统等。

分形是几何外形，与传统几何相比具有以下特点。

第一，从整体看，分形几何图形是处处不规则的。例如，海岸线和山川形状，它们处处无规则可量。

第二，在各种尺度上，图形都有同样程度的不规则性。无论是从远处观察，还是从近处观察，分形整体看起来都是一个模样，它是自相似的。对同一个分形事物，无论是将它放大还是将它压缩，它的形态、复杂程度、不规则性都不会变化。从不同的测量尺度去观察它，它在许多方面都是相似的。整体中的部分，从远处看是不成形的，但从近处看，则可以发现其轮廓分明，形状也大致和整体的形状相似。

第三，无标度性。标度就是尺度，是测量的单位。尺度在我们的日常生活中是十分重要的。我们遇到一个人时，会估计他有多高、有多重，年龄有多大等，是我们认识和描述这个人很重要的参数。尺度不恰当就得不到正确的结论。如果我们用“尺”去丈量长城，或者用“寸”去测量细菌都是不恰当的。俗话说，海水不可斗量，在这个世界中，掌握特征尺度（特征长度、特征容积、特征时间）是理解事物的关键，只有选择了恰当的尺度，才能正确地描述事物。在通常情况下，每一个事物都有其特征尺度，事物的性质也随尺度的改变而改变，因而不同的事物有不同的特性。具有特征尺度的事物是普遍存在的，这是一个处处呈现出标度特征的世界。

那么，无标度的事物又是怎么回事呢？科学家们发现，一个具有无限嵌套自相似结构的事物是无标度的，它没有特征尺度。自相似产生了一个重要结果——无标度性。具有相似结构的事物从不同的测量尺度上看，竟然是差不多的。当改变测量单位或尺度时，其结果仍是一样的。如果用照相机对它们拍照，即使采用不同放大倍数的镜头，拍出来的照片依然是相似的，并且从照片上我们无法判断所用照相机的放大倍数。这就是无标度性。海岸线是自然界中的一个分形实例，具有自相似结构，是典型的无标度对象。当从飞机上俯瞰一个国家的海岸线时，我们会发现，在不同高度上看到的海岸线的形状是大致相同的。例如，在10 000米拍摄的海岸线照片，与在2 000米高空拍摄的照片其实是差不多的。两者的视野不同，但两张照片在统计意义上是相似的。从远处、大范围看到的不规则程度，与从近处、小范围看到的不规则程度几乎相同。这就表明，海岸线是分形系统，具有无穷层次的自相似性，具有标度不变性，是无标度对象。

在我们的周围，分形无处不在（如图4.4所示），一切复杂系统都具有分形特征，因此，我们在认识、研究和描述事物时，不能忽视事物的自相似性和无标度性。分形打破了人们长期以来按特征尺度去思考事物的习惯。

（2）分数维

在传统的欧几里得几何中，一个几何对象的维数等于确定其中一个点的位置所需要的独立坐标数目。在欧几里得空间中，维数都是整数。点是零维，直线是一维，面是二维，体是三维。而分形维数可以取分数，简称分数维。

我们可以这样来建立分数维的概念，首先分别画一条线段、一个正方形和一个立方体，它们的边长都是1。将它们的边长二等分，此时原图的线长缩短为原来的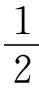，原图被等分为若干个相似的图形，线段、正方形和立方体分别被等分为2，22和23个相似的子图形，其中指数1，2，3正好等于与图形相应的拓扑维数。一般来说，如果某图形是由N个把原图缩小为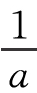的相似图形所组成的，则有下面的关系式成立：

(www.xing528.com)

其中D称为相似性维数，它可以是整数，也可以是分数。

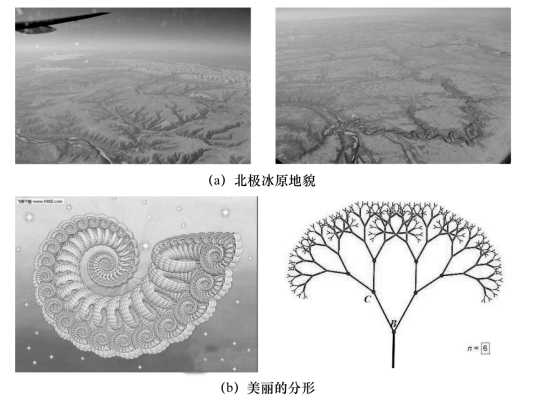
图4.4　分形无处不在

1967年，曼德布罗特研究了“英国的海岸线有多长”这个长期困扰着数学家的难题（如图4.5所示）。他认为，海岸线的长度，取决于所用的测量标尺的长度。标尺越短，就越能测出海岸线的弯曲处，所测出的总长度也就越长。由此可见，我们在研究海岸线的问题时，应该关注的是它有多复杂，而不是它有多长。曼德布罗特研究发现，海岸线长度是以它的分数维来增加的。分形的概念正是在解决了这个难题之后才创立的。

图4.5　英国海岸线到底有多长

曼德布罗特采用瑞典数学家柯克（Cauchy）发现的一种曲线——“柯克曲线”作为海岸线的数学模型。以一个等腰三角形的每条边中间的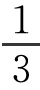为底线向外侧作一个小的等腰三角形，然后抹去这个小三角形的底边，就能得到一条新的闭折线，在新的曲线的每条边上重复上述作图过程，如此无限重复下去，所得到的极限图形就是柯克曲线。如图4.6所示，为一条边的作图过程。

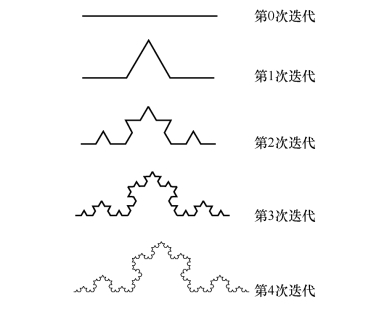
图4.6　柯克曲线图

设原三角形的边长为1，我们容易看出柯克曲线的长度是一个无穷大的数，而它所包围的面积则是一个有限数，等于原三角形面积的1.6倍。一块有限面积具有无限长的边界，曼德布罗特认为这种奇怪的现象是由边界曲线的“无限折曲”引起的。正是通过对这种“无限折曲”过程的深入研究，曼德布罗特引进了分数维数的概念。

对柯克曲线，D未知，但N和a的值可以确定：N=4，a=3。这两个数字对每一步近似曲线的每一小段都成立，故对整个柯克曲线也成立。由式（4.4.18）可得

D=log N/log a=log 4/log 3≈1.261 8，

也就是说，海岸线是一个具有分数维的几何实体。

有了柯克曲线之后，人们发现，山脉、河流、闪电所描绘出来的曲线也是处处连续，又处处不光滑的。曼德布罗特指出，柯克曲线是粗糙且生动的海岸线模型。

20世纪数学在集合概念上有两次与空间维度相关的飞跃。分别是发生在上半世纪的从有限维到无穷维的飞跃，以及发生在下半世纪的从整数维到分数维的飞跃。自相似性是分形的本质，分数维是量度自相似的特征量。有效地挖掘分数维所包含的信息并加以利用，无论在理论上还是应用上都具有重要意义。

目前，分形理论在众多科学领域中取得了成功的应用。例如，在地球科学中用于海岸线与河流的分形、地震与矿藏的分形；在材料科学中用于材料裂纹的分形；在计算机科学中用于分形图形的处理和分形图形的压缩；在经济和金融领域用于股票价格的预测，以及经济收入分配的分数维和基尼系数的计算；在管理科学中，借用自相似概念描述的一种新的生产方式，建立分形企业和供应链的管理模式等。

此外，分形理论提出了客观世界中部分与整体之间的辩证关系，即整体与部分之间具有相似性，从而使人们对整体与部分之间的关系的理解从线性发展到了非线性，为人们从有限认识无限提供了一种新的方法论。