【摘要】：考情提要考点精讲（一）双因素方差分析及其类型双因素方差分析：方差分析中涉及两个分类型自变量。表10-14品牌与地区双因素方差分析表表10-14中的行因素，即品牌因素；列因素，即地区因素。与无交互作用的双因素方差分析方法类似，有交互作用的双因素方差分析也需要提出假设、构造检验统计量、做出统计决策等步骤。有交互作用的双因素方差分析表如表10-15所示。
1.【解析】
（1）计算结果如表10-22所示。
表10-22 方差分析表
（2）由于P值=0.000＜α=0.05，拒绝原假设。表明不同品种的种子对小麦产量的影响有显著差异。
P值=0.000＜α=0.05，拒绝原假设。表明不同施肥方式对小麦产量的影响有显著差异。
P值=0.3793＞α=0.05，不拒绝原假设。没有证据表明不同的品种和不同的施肥方式对小麦产量有交互影响。
2.【解析】
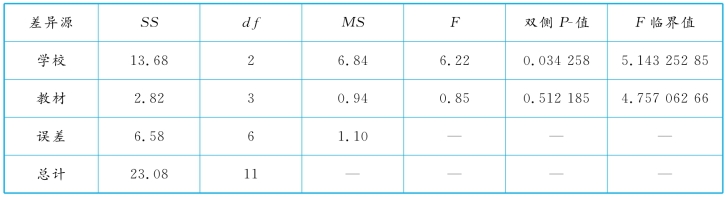
（1）填出表格中空白的数字如表10-23所示。
表10-23 方差分析表
(www.xing528.com)
（2）为了检验学校和教材对教学效果的影响，需要对这两个因素分别提出如下假设。对行因素（学校）提出的假设：
式中，μi为行因素的第i个水平的均值。
对列因素提出的假设：
式中，μj为列因素的第j个水平的均值。
（3）根据方差分析表的计算结果得出以下结论。
由于FR=6.22＞5.14325285，因此拒绝原假设H0，表明学校对教学效果有显著影响。
由于FC=0.85＜4.75706266，因此不拒绝原假设H0，表明不能认为教材对教学效果有显著影响。
（4）上述数据不能进行有交互作用的方差分析，因为学校和教材两个因素都取定时对应的数据只有一个。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
