随机变量及其分布：关键考点解析

考情提要

考点精讲

（一）随机变量

随机变量：定义在样本空间Ω上的实值函数X=X（ω）称为随机变量，常用大写字母X，Y，Z等表示随机变量，其取值用小写字母x，y，z等表示。

按照随机变量的特性，通常可把随机变量分为两类，即离散型随机变量和连续型随机变量。

（1）离散型随机变量。

如果随机变量X的所有取值都可以逐个列举出来，则称X为离散型随机变量。

（2）连续型随机变量。

如果随机变量X的所有取值无法逐个列举出来，而是取数轴上某一区间内的任一点，则称X为连续型随机变量。

（二）随机变量的分布函数

设X为一个随机变量，对任意实数x，称F（x）=P（X≤x）为X的分布函数。且称X服从F（x），记为X～F（x）或FX（x）。

任一分布函数F（x）都具有如下三条基本性质：

（1）单调性。F（x）是定义在整个实数轴（-∞，+∞）内的单调非减函数，即对任意的x1＜x2，有F（x1）≤F（x2）。

（2）有界性。对任意的x，有0≤F（x）≤1，F（-∞）=0，F（+∞）=1。

（3）右连续。F（x）是x的右连续函数。

以上三条基本性质是分布函数必须具有的性质，还可以证明：满足这三个基本性质的函数可以是某个随机变量的分布函数，从而这三个基本性质成为判别某个函数是否能成为分布函数的充要条件。

知识点补充

对任意的实数a＜b，有

（1）P（a＜X≤b）=F（b）-F（a）；

（2）P（X=a）=F（a）-F（a-0）；

（3）P（X≥b）=1-F（b-0）；

（4）P（X＞b）=1-F（b）；

（5）P（a＜X＜b）=F（b-0）-F（a）；

（6）P（a≤X≤b）=F（b）-F（a-0）；

（7）P（a≤X＜b）=F（b-0）-F（a-0）。

特别地，如果函数在a，b处连续，有

（三）离散型随机变量的分布

概率函数：在同一组条件下，如果每次试验可能出现这样或那样的结果，并且所有的结果都能列举出来，即X的所有可能值x1，x2，…，xn都能列举出来，而X的可能值x1，x2，…，xn具有确定概率P（x1），P（x2），…，P（xn），其中P（xi）=P（X=xi），则X称为P（X）的随机变量，P（X）称为随机变量X的概率函数。

设X是离散型随机变量，它的所有可能的取值为x1，x2，…，xn，…，则称P（X=xi）=p（xi），i=1，2，…，n，…为X的概率分布列或简称为分布列，记为X～pi，分布列也可以用如下列表来表示

或记成

分布列的基本性质

（1）非负性。p（xi）≥0，i=1，2，…。

（2）正则性。。

由离散型随机变量X的分布列可以得到X的分布函数为

知识点补充

（1）求离散型随机变量的分布列应该注意：

①确定随机变量的所有可能取值；

②计算每个取值点的概率。

（2）求离散型随机变量的分布函数应该注意：

①F（x）是递增的阶梯函数；(www.xing528.com)

②其间断点均为右连续点；

③其间断点即为X的可能取值点；

④其间断点的跳跃高度是其对应的概率值。

【例5.12】

已知X的分布列如下

求X的分布函数。

【解析】

【例5.13】

离散型随机变量ξ的分布列为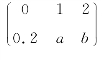，其中a，b是未知数，如果ξ取1的概率和取2的概率相等，则a=（　）。

A.0.2

B.0.3

C.0.4

D.0.5

【答案】C

【解析】根据分布列的正则性可以得到a=0.4。

（四）连续型随机变量的分布

连续型随机变量的一切可能取值充满某个区间（a，b）或整个实数轴，在这个区间内有无穷不可列个实数，因此连续型随机变量的概率分布不能再用分布列形式表示，而要改用概率密度函数表示。

设随机变量X的分布函数为F（x），如果存在实数轴上的一个非负可积函数p（x），使得对任意实数x有

则称p（x）为X的概率密度函数，简称为密度函数，或称密度。

密度函数的基本性质：

（1）非负性。p（x）≥0。

（2）正则性。（含有p（x）的可积性）。

以上两条基本性质是密度函数必须具有的性质，也是确定或判别某个函数是否能成为密度函数的充要条件。

知识点补充

（2）F（x）是（-∞，+∞）内的连续函数；

（3）P（X=x）=F（x）-F（x-0）=0；

（5）P（a≤X≤b）=P（a＜X≤b）=P（a≤X＜b）=P（a＜X＜b）；

（6）密度函数X～p（x）不唯一。

真题精练

1.设随机变量的概率密度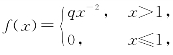则q=（　）。

A.1／2

B.3／2

C.-1

D.1

【2017浙江工商大学】

2.设离散型随机变量ξ的分布律为，k=0，1，2，3，…，则常数A应为（　）。

【2011浙江工商大学】

3.设X的概率密度函数为f（x），则f（x）一定满足（　）。

【2017山东大学】