使用数学归纳法证明不等式的方法与步骤

1.B 2.D 3.B 4.D 5.C 6.C

7.由等式的特点知,

当n=1时,左边从第一项起,一直加到cos(2n-1)α,故左边计算所得的项是

8.因为n为正奇数,假设n=2k-1成立后,需证明的应为n=2k+1时成立.

9.因为f(2)=0,f(3)=2,f(4)=5,f(5)=9,

每增加一条直线,交点增加的个数等于原来直线的条数,

所以f(3)-f(2)=2,f(4)-f(3)=3,f(5)-f(4)=4,…,f(n)-f(n-1)=n-1.

相加,得f(n)-f(2)=2+3+4+…+(n-1)=

所以

综上所述

10.(1)当n=1时,左边=,右边=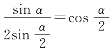,左边=右边,等式成立.

(2)假设当n=k(k≥1,k∈N*)时,等式成立,

即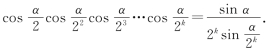

当n=k+1时,=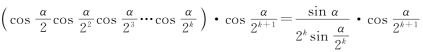

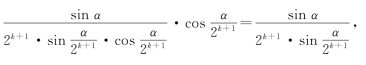
即当n=k+1时,等式也成立.(www.xing528.com)

由(1)(2)知,等式对n∈N*均成立.

11.(1)当m=1时,

a4m+1=a5=a4+a3=(a3+a2)+(a2+a1)=(a2+a1)+2a2+a1=3a2+2a1=3+0=3,

即当m=1时,第4m+1项能被3整除.

(2)假设当m=k(k≥1)时,a4k+1能被3整除.

则当m=k+1时,

a4(k+1)+1=a4k+5=a4k+4+a4k+3=2a4k+3+a4k+2=2(a4k+2+a4k+1)+a4k+2=3a4k+2+2a4k+1.

显然,3a4k+2能被3整除,又由假设知a4k+1能被3整除,

所以3a4k+2+2a4k+1能被3整除.即当m=k+1时,a4(k+1)+1也能被3整除.

由(1)(2)知,对于n∈N*,数列{an}中的第4m+1项能被3整除.

12.(1)当n=1时,n2-n+2=1-1+2=2,而1个圆把平面分成两部分,所以n=1时,命题成立.

(2)假设当n=k(k≥1)时,k个圆分平面为(k2-k+2)个部分.

则当n=k+1时,第(k+1)个圆与前k个圆有2k个交点,这2k个交点分第(k+1)个圆为2k段,每一段都将原来所在的平面一分为二,故增加了2k个平面部分,共有(k2-k+2)+2k=(k+1)2-(k+1)+2(个)部分.所以对n=k+1时,命题也成立.

由(1)(2)可知,这n个圆分平面为(n2-n+2)个部分.