使用数学归纳法证明不等式的6种方法

数学归纳法是用来证明与自然数有关命题的一种有效方法,在高中数学中,经常会以数列和函数为知识载体,构造一些与自然数有关的命题,数学归纳法是证明它们的有效手段,但不是唯一手段.

数学归纳法基本步骤:

(1)证明当n=n0(初始值)时,命题成立;

(2)假设n=k(k≥n0,k∈N*)时成立,证明n=k+1时命题也成立.

由(1)(2)⇒原命题对n≥n0(n∈N*)时都成立.

注:(1)正整数是连续的,即在正整数n之后的正整数一定是n+1;

(2)两个步骤缺一不可.

方法简述

1.比较法

例1 求证

点拨 这类和正整数有关问题的证明,常采用数学归纳法.

证明 (1)当n=2时,左式=,右式=,左式>右式.

所以当n=2时,不等式成立.

(2)假设当n=k(k≥2)时,不等式成立,即

则当n=k+1时,

因为,所以=右式.

由不等式的传递性,可得左式>右式.

所以当n=k+1时,不等式也成立.

由(1)(2)可得,对一切n≥2,n∈N*,不等式都成立.

反思 本题在由n=k到n=k+1时的推证过程中,关键的是证明为证此,我们采用了不等式证明方法中的比较法.

2.放缩法

放缩是一种技巧性较强的不等变形,必须时刻注意放缩的跨度,做到“放不能过头,缩不能不及”.

例2 求证

点拨 用数学归纳法证明,要完成两个步骤,这两个步骤是缺一不可的.但从证题的难易程度来分析,证明第二步是难点和关键,要充分利用归纳假设,做好命题从n=k到n=k+1的转化,这个转化要求在变化过程中结构不变.

证明 (1)当n=2时,左边=,不等式成立.

(2)假设当n=k(k≥2,k∈N*)时命题成立,即

则当n=k+1时,

所以则当n=k+1时,不等式也成立.

由(1)(2)可知,原不等式对一切n≥2,n∈N*均成立.

反思 本题由n=k到n=k+1时的推证过程中:

(1)一定要注意分析命题的结构特征,即由n=k到n=k+1时不等式左端项数的增减情况;

(2)应用了放缩技巧:

例3 求证

点拨 在由n=k到n=k+1时的推证过程中,可使用均值定理进行放缩.

证明 (1)当n=2时,左边=,右边=22.

∴左边<右边.

∴当n=2时,原不等式成立.

(2)假设当n=k时,不等式成立,即

当n=k+1时,

∴当n=k+1时,原不等式成立.

由(1)(2)知,对n≥2的任何自然数,原不等式成立.

反思 本题在证明时,将它转化为

通过放缩证得n=k+1时也成立,从而证明了结论.

3.单调性

例4 已知数列{an}的各项都是正数,且满足:

(1)求证:an<an+1<2(n∈N);

(2)求数列{an}的通项公式an.

点拨 本题用数学归纳法证明,但可采用两种不同的方式:一是作差比较法;二是利用函数的单调性.

解答 (1)证明:当n=1时

则0<a1<a2<2.

假设当n=k时有ak<ak+1<2成立.

令在区间[0,2]上单调递增,

所以由假设有f(ak)<f(ak+1)<f(2),

即

也即当n=k+1时,ak+1<ak+2<2成立,

所以对一切n∈N,有ak<ak+1<2.

(2)因为

所以2(an+1-2)=-(an-2)2.

令bn=an-2,则

因为b0=-1,所以,

即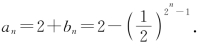

反思 本题也可先求出第(2)问,即数列{an}的通项公式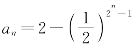,然后利用函数的单调性和有界性,来证明第(1)问的不等式.但若这样做,则无形当中加大了第(1)问的难度,显然不如用数学归纳法证明来得简捷.

4.转化法

例5 数列{an}的通项公式为an=3n+2,将数列{an}中的第2,4,8,…,2n项依次取出,按原来的顺序组成一个新数列{bn},记其前n项和为Sn,Tn=n(9+an),当n≥4时,求证:Sn>Tn.

点拨 要证Sn>Tn,只需证3×2n+1+2n-6>3n2+11n,即证2n+1>n2+3n+2.这就证明了原不等式的等价不等式,从而将命题简化.

证明 ∵an=3n+2,∴a2n=3×2n+2,

∴Sn=a2+a4+a8+…+a2n=3(2+4+8+…+2n)+2n=3×2n+1+2n-6.

而Tn=n(9+an)=3n2+11n.

要证Sn>Tn,只需证3×2n+1+2n-6>3n2+11n,

即证2n+1>n2+3n+2.

用数学归纳法来证明:

(1)当n=4时,S4=98,T4=92,S4>T4成立.

(2)假设当n=k(k≥4)时,结论成立,就是2k+1>k2+3k+2,那么当n=k+1时,

∵k≥4,∴(k+2)(k-1)>0.∴2k+2>(k+1)2+3(k+1)+2.(www.xing528.com)

这就是说,当n=k+1时,Sn>Tn也成立.

由(1)(2)知,对n≥4,Sn>Tn都成立.

反思 本题用数学归纳法证明2n+1>n2+3n+2,第二步采用的是作差比较法:作差—利用归纳假设—变形(因式分解)—定号.这比通常的“作差—变形—定号”多了利用归纳假设这一步,这是因为归纳假设是用数学归纳法证明命题时所必需的.

易错解读

易错点1 对假设设而不用.

用数学归纳法证明时,证明第二步要充分利用归纳假设,做好命题从n=k到n=k+1的转化,这个转化要求在变化过程中结构不变.

例6 用数学归纳法证明

证明 错误的证法:(1)当n=1时,左边=1.

右边=×1×(1+1)×(2×1+1)=1.

所以等式成立.

(2)假设当n=k时等式成立,即

那么当n=k+1时,为

也就是说当n=k+1时,等式成立.

由(1)(2)知,对任何n∈N*等式成立.

正确的证法:(1)当n=1时,左边=1.

右边=×1×(1+1)×(2×1+1)=1.

所以等式成立.

(2)假设当n=k时等式成立,即

那么当n=k+1时,为

即当n=k+1时,等式成立.

由(1)(2)知,对任何n∈N*等式成立.

反思 用数学归纳法证明第二步时,在从“k”到“k+1”的过程中,必须把n=k的命题作为已给定的条件,要在这个条件基础上去导出n=k+1时的命题.所以在推导过程中,必须把n=k时的命题用上,本解法错因是对假设设而不用.

易错点2 机械套用数学归纳法中的两个步骤导致错误.

数学归纳法虽有固定的步骤,但要注意其中变量n的范围,要根据范围变化调整证明过程.

例7 当n为正奇数时,7n+1能否被8整除?若能,用数学归纳法证明;若不能,请举出反例.

证明 当n为正奇数时,7n+1能被8整除.

错误的证法:(1)当n=1时,7+1=8能被8整除.命题成立.

(2)假设当n=k时命题成立.即7k+1能被8整除.

则当n=k+1时,7k+1+1=7(7k+1)-6不能被8整除.

由(1)(2)知,当n为正奇数时,7n+1不能被8整除.

正确的证法:(1)当n=1时,7+1=8能被8整除.命题成立.

(2)假设当n=k时命题成立,即7k+1能被8整除.

当n=k+2时,7k+2+1=72(7k+1)+1-72=49(7k+1)-48.

因为7k+1能被8整除,48能被8整除,所以7k+2+1能被8整除.

所以当n=k+2时,命题成立.

由(1)(2)知,当n为正奇数时,7k+1能被8整除.

反思 机械套用数学归纳法中的两个步骤而忽略了n是正奇数的条件,证明前要看准已知条件.

易错点3 没有搞清从“k”到“k+1”的跨度.

注意分析清楚命题的结构特征,即由n=k到n=k+1时不等式左端项数的增减情况.

例8 求证

证明 错误的证法:(1)当n=1时,左边=,不等式成立.

(2)假设当n=k时命题成立,即

则当n=k+1时

所以当n=k+1时,不等式成立.

由(1)(2)知,原不等式成立.

正确的证法:(1)当n=1时,左边=,不等式成立.

(2)假设当n=k时命题成立,即

则当n=k+1时,

所以当n=k+1时,不等式成立.

由(1)(2)知,原不等式成立.

反思 上述错误证明中,从“k”到“k+1”的跨度,只加了一项是错误的,分母是相邻的自然数,故应是,跨度是三项.

经典训练

1.某个命题:(1)当n=1时,命题成立.(2)假设n=k(k≥1,k∈N*)时成立,可以推出n=k+2时也成立,则命题对(　)成立.

A.正整数　B.正奇数　C.正偶数　D.奇数

2.设,在利用数学归纳法证明时,从n=k到n=k+1需添的项为(　).

A.　B.　C.D.

3.记凸k边形的内角和为f(k),则凸k+1边形的内角和f(k+1)=f(k)+A,则A=(　).

A.　B.π　C.2π　D.

4.在数列{an}中,前n项和,先算出数列的前4项的值,再根据这些值归纳猜想数列的通项公式是(　).

A.　B.

C.　D.

5.已知f(n)=(2n+7)·3n+9,存在自然数m,使得对任意n∈N*,都能使m整除f(n),则最大的m的值为(　).

A.30　B.26　C.36　D.6

6.在数列{an}中,且Sn=n(2n-1)an,通过求a2、a3、a4猜想an的表达式为(　).

A.　B.

C.　D.

7.用数学归纳法证明,在验证n=1等式成立时,左边计算所得的项是_________.

8.用数学归纳法证明“当n为正奇数时,xn+yn能被x+y整除”,当第二步假设n=2k-1(k∈N*,k≥1)命题为真时,进而需证n=_________时,命题亦真.

9.设平面内有n条直线(n≥2),其中有且仅有两条直线互相平行,任意三条直线不过同一点.若用f(n)表示这n条直线交点的个数,则f(4)=________;当n>4时,f(n)=________(用n表示).

10.用数学归纳法证明:若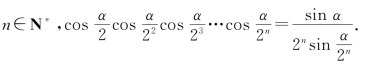

11.已知数列{an}满足a1=0,a2=1,当n∈N*时,an+2=an+1+an,求证:数列{an}的第4m+1项(m∈N*)能被3整除.

12.平面上有n个圆,每两圆交于两点,每三圆不过同一点,求证:这n个圆分平面为n2-n+2个部分.