排序不等式是基本而重要的不等式,许多重要的不等式可以借助排序不等式得到证明,例如:算术—几何平均不等式、柯西不等式、切比雪夫总和不等式.
一般地,设有两组实数:a1,a2,a3,…,an与b1,b2,b3,…,bn,且它们满足:
a1≤a2≤a3≤…≤an,b1≤b2≤b3≤…≤bn,
若c1,c2,c3,…,cn是b1,b2,b3,…,bn的任意一个排列,则和数a1c1+a2c2+…+ancn在a1,a2,a3,…,an与b1,b2,b3,…,bn顺序时最大,反序时最小,即:
a1b1+a2b2+…+anbn≥a1c1+a2c2+…+ancn≥a1bn+a2bn-1+…+anb1,
当且仅当a1=a2=…=an或b1=b2=…=bn时,等号成立.
方法简述
1.公式法
例1 设a1,a2,…,an是n个互不相同的正整数,求证:
点拨 由于a1,a2,…,an是n个互不相同的正整数,因此它们可以进行排序;同时,观察需要证明的不等式,可以联想到a1,a2,…,an对应的另一列数是![]() ,由此可以联想到应用排序不等式.
,由此可以联想到应用排序不等式.
解答 设b1,b2,…,bn是a1,a2,…,an的一个排列,且满足b1<b2<…<bn.
因为b1,b2,…,bn是互不相同的正整数,所以b1≥1,b2≥2,…,bn≥n.
又![]()
故由排序不等式:乱序和≥反序和,得
所以原不等式成立.
反思 值得注意的是不能直接假设a1≤a2≤…≤an,会影响两列数的乘积之和是顺序和、乱序和还是反序和,所以需要定义a1,a2,…,an的大小关系.
例2 设a1,a2,…,an是1,2,…,n的一个排列,求证:
点拨 通过观察,把a1,a2,…,an-1与a2,a3,…,an分别看作两组有大小顺序的数组,联想应用排序不等式进行证明.
证明 设b1,b2,…,bn-1是a1,a2,…,an-1的一个排列,且b1<b2<…<bn-1;c1,c2,…,cn-1是a2,a3,…,an的一个排列,且c1<c2<…<cn-1,则![]() ,且b1≥1,b2≥2,…,bn-1≥n-1,c1≤2,c2≤3,…,cn-1≤n.
,且b1≥1,b2≥2,…,bn-1≥n-1,c1≤2,c2≤3,…,cn-1≤n.
由排序不等式:乱序和≥反序和,得
所以原不等式成立.
反思 应用排序不等式,必须取两组个数相同、便于大小排序的数,此时有两种情形:一是知道各数的大小顺序,二是不知道各数的大小顺序,但由于不等式是对称不等式,可以在不失一般性的情况下,假定各数的大小顺序.
2.构造法
构造法体现了化归的思想.在构造法运用过程中,常常把一个个零散的知识点(构造元素)由表及里、由浅入深地集中和联系,通过恰当的方法加以处理化归为已有的认识,从而形成了一种构造法解题的手段.
用构造法解题的巧妙之处在于不是直接去解决所给的原问题,而是构造一个与原问题有关的辅助新问题,这里引出的新问题并非为了它本身,而是希望通过它的解决来帮助解决原问题.如果构造的新问题比原问题更简单、更直观,那么这种思考问题的方法就会成功.
例3 设a1、a2、a3都是正数,求证![]()
点拨 观察需要证明的不等式,我们需要构造两组数,并且这两组的乘积可以出现a1、a2、a3,满足不等式的右端;观察不等式的左端,我们不妨设a1≤a2≤a3,构造a1a2≤a1a3≤a2a3和![]() ,应用排序不等式证明即可.
,应用排序不等式证明即可.
证明 设a1≤a2≤a3,则![]()
由排序不等式:顺序和≥乱序和,得
所以原不等式成立.
反思 应用排序不等式证明不等式,必须构造出两列个数相等的数组,并且要利用数组的大小关系进行解题.因此,比较数组的大小关系是解题的基础.灵活构造两列数组,也是解题的关键所在.并且需要注意,在未给出数组大小关系的时候,要不失一般性地对数组进行大小顺序的排列.
3.累加法
根据排序不等式:顺序和≥乱序和≥反序和,我们可以发现乱序和的形式不止一种,所以我们经常利用这一点构造多个不等式进行累加,从而得到所需要的不等式,这是运用排序不等式的常用策略.
例4 在△ABC中,求证![]()
点拨 可构造△ABC的边和角的序列,应用排序不等式来证明.
证明 设a≤b≤c,于是A≤B≤C.
由排序不等式,得
aA+bB+cC≥aA+bB+cC,
aA+bB+cC≥bA+cB+aC,(https://www.xing528.com)
aA+bB+cC≥cA+aB+bC.
上述三式相加,得
3(aA+bB+cC)≥(a+b+c)(A+B+C)=π(a+b+c).
则![]()
又由0<b+c-a,0<a+b-c,0<a+c-b,有
0<A(b+c-a)+C(a+b-c)+B(a+c-b)=a(B+C-A)+b(A+C-B)+c(A+B-C)=a(π-2A)+b(π-2B)+c(π-3C)=(a+b+c)π-2(aA+bB+cC).
所以![]()
由①②得原不等式成立.
反思 根据三角形边和角之间的关系,并注意到aA+bB+cC的形式,我们很容易联想到应用排序不等式;若注意到π=A+B+C,则问题迎刃而解.
易错解读
易错点 不能作适当转化.
应用排序不等式解题的关键在于构造出它所需要的两组数列,然而构造数列的过程却奥妙无穷,需要不断分析探讨,才能积累经验,运用得法.
例5 设a、b、c为正数,求证![]()
证明 原不等式等价于![]()
不妨设a≤b≤c,则![]()
由排序不等式:顺序和≥乱序和,得
即![]()
反思 本题通过观察发现,我们可以将不等式转化为![]()
![]() 的形式,进而应用排序不等式进行解题.有些需要证明的不等式并不是直接给出排序不等式的乘积之和的形式,这时就需要我们对不等式从结构上观察进行适当的变形,为使用排序不等式创造条件.
的形式,进而应用排序不等式进行解题.有些需要证明的不等式并不是直接给出排序不等式的乘积之和的形式,这时就需要我们对不等式从结构上观察进行适当的变形,为使用排序不等式创造条件.
经典训练
1.设a1,a2,…,an都是正数,b1,b2,…,bn是a1,a2,…,an的任意一个排列,则![]()
![]() 的最小值是( ).
的最小值是( ).
A.1 B.n C.n2 D.无法确定
2.已知a、b、c为正数,P=![]() ,Q=abc,则P、Q的大小关系是( ).
,Q=abc,则P、Q的大小关系是( ).
A.P>Q B.P≥Q C.P<Q D.P≤Q
3.![]() 的取值范围是( ).
的取值范围是( ).
A.(21,+∞) B.(61,+∞) C.(4,+∞) D.(3n-2,+∞)
4.一组实数为a1、a2、a3,设c1、c2、c3是另一组数b1、b2、b3的任意一个排列,则a1c1+a2c2+a3c3的( ).
A.最大值为a1b1+a2b2+a3b3,最小值为a1b3+a2b2+a3b1
B.最大值为a1b2+a2b3+a3b1,最小值为a1b3+a2b1+a3b2
C.最大值与最小值相等,为a1b1+a2b2+a3b3
D.以上答案都不对
5.若![]() ,则
,则![]() 2γ)的符号为( ).
2γ)的符号为( ).
A.F>0 B.F<0 C.F≥0 D.F≤0
6.已知a、b、c为正实数,则a2(a2-bc)+b2(b2-ac)+c2(c2-ab)_________0(填“<”“>”“≤”“≥”).
7.设a、b都是正数,若![]() ,则二者的关系是________.
,则二者的关系是________.
8.设正数a、b、c的乘积![]() 的最小值为________.
的最小值为________.
9.设x1≥x2≥…≥xn,y1≥y2≥…≥yn,求证![]() 其中z1,z2,…,zn是y1,y2,…,yn的任意一个排列.
其中z1,z2,…,zn是y1,y2,…,yn的任意一个排列.
10.利用排序原理证明切比雪夫总和不等式:
若a1≤a2≤…≤an且b1≤b2≤…≤bn,则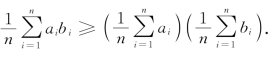
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




