深入理解柯西不等式及其四大定理

定理1:二维形式的柯西不等式

设a、b、c、d均 为实数,则

(a2+b2)(c2+d2)≥(ac+bd)2,

当且仅当ad=bc时,等号成立.

定理2:(柯西不等式的向量形式)

设为平面上的两个向量,则,当且仅当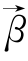是零向量,或存在实数k,使时,等号成立.

定理3:(三角形不等式)

设x1、y1、x2、y2、x3、y3为任意实数,则

定理4:(柯西不等式的推广形式)

设n为大于1的自然数,ai、bi(i=1,2,…,n)为任意实数,则

当且仅当中有一个为零时等号成立.

方法简述

1.公式法

从形式结构上看,柯西不等式大的一边是两个向量的模的积的形式,小的一边是向量数量积的坐标运算的平方形式,只需简记为“方和积大于积和方”.等号成立条件比较特殊,要牢记.

例1 若3x+4y=2,试求x2+y2的最小值及最小值点.

点拨 由柯西不等式,得(x2+y2)(32+42)≥(3x+4y)2即可求出最值.

解答 由柯西不等式,得(x2+y2)(32+42)≥(3x+4y)2.

则25(x2+y2)≥4,所以

当且仅当时,等号成立.

为求最小值点,需解方程组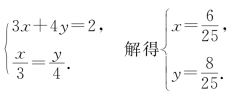

即当时,x2+y2的最小值为,最小值点为

反思 柯西不等式也能用来解决某些最值问题,但要注意等号成立的条件.

例2 设a、b、c为正数,求证:

点拨 如果要运用柯西不等式,就要联想到小的一边是“积和方”形式,另一边要看成“方和积”就自然分析出只要在所需证明的不等式两边同乘a+b+c即可.

证明 两边同乘a+b+c,即

而另一边要看成“方和积”,则应用柯西不等式,得所以

反思 要使用柯西不等式,常常要根据给出的式子构造“积和方”和“方和积”,方能解决问题.

2.构造法

构造法的本质就是——依据某些数学问题的条件或结论所具有的典型特征,用已知条件中的元素为“元件”,用已知数学关系为“支架”,在思维过程中构造出一系列相关的数学对象、一系列新的数学形式;或利用问题的特殊性,为待解决问题构造一个合理的数学框架,从而使数学问题成功解决.

在解数学题中,恰当地、合理地运用构造法,不仅能够收到简洁明快、出奇制胜的效果,同时还有利于培养同学们的抽象思维能力和发散思维能力,因而这种数学解题方法具有独特的数学价值和解题意义.

例3 求证:(a3+b3+c3+d3)2≤4(a6+b6+c6+d6).

点拨 常数4恰好就是每个括号中加数的个数,此时通常把4写成“12+12+12+12”,再用柯西不等式.

证明 ∵4=12+12+12+12,∴4(a6+b6+c6+d6)=(12+12+12+12)(a6+b6+c6+d6).

由柯西不等式,得

(a3+b3+c3+d3)2≤(12+12+12+12)(a6+b6+c6+d6).

反思 在不等式中含有常数n,这个常数一般与柯西不等式中向量的维数有关,通常把n写成“12+12+12+…+12”的形式或“1+1+…+1”的形式.

例4 求实数x、y的值,使得达到最小值.

点拨 本题需要把看成是不等式中向量模的平方,构造另一模的平方.

解答 构造的顺序为先把最繁的式子2x+y-6对应的坐标设为1,再考虑x+y-3乘-2就可以把x抵消,因此-2就是x+y-3对应坐标,最后看1×(2x+y-6)+(-2)×(x+y-3)=-y,因此y-1对应的坐标为1.

由柯西不等式,得

所以

当且仅当时取等号.

所以当时,(y-1)2+(x+y-3)2+(2x+y-6)2取最小值.

反思 解决上述类型的问题需要对柯西不等式非常熟悉,才能将所求问题和柯西不等式联系起来,其中构造的过程有难度.

例5 若,试求函数的最大值,并求出相应的x的值.

点拨 将本题中f(x)看成是两个向量的数量积,就可以通过柯西不等式的向量形式求解最值.

解答 设,则

当且仅当时,取等号,

此时

解得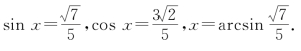

所以当时,函数取最大值52.

反思 柯西不等式的各种形式在解题中都有不同的作用,灵活构造柯西不等式的适当形式在这类问题中尤为重要.

3.换元法

换元的实质是转化,关键是构造元和设元,理论依据是等量代换,目的是变换研究对象,将问题移至新对象的知识背景中去研究,从而使非标准型问题标准化、复杂问题简单化,变得容易处理.

例6 设正数x、y、z满足3x+4y+5z=1.

求的最小值.

点拨 关键是先应用换元法构造柯西不等式因式,再用不等式解题.

解答 设x+y=a,y+z=b,z+x=c,

则

代入3x+4y+5z=1得a+3b+2c=1.

由柯西不等式,得(www.xing528.com)

当且仅当时,等号成立.

所以的最小值为

反思 本题通过换元,将x、y、z三个变量转化为a、b、c,使原来复杂的式子得以简化,因而就容易想到利用柯西不等式来解题.

易错解读

易错点1 不能熟练构造柯西不等式.

很多重要的不等式都可以由柯西不等式导出,而利用柯西不等式的技巧有很多,如常数的巧拆、结构的巧变、巧设数组等.

例7 设a、b、c均为正数,且a+b+c=12,则的最小值为________.

解答 由柯西不等式,得

∵a+b+c=12,∴(1+3+5)2≤

当且仅当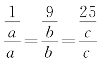时取等号,则的最小值为

反思 本题主要考查了函数的值域,以及柯西不等式的应用,解题的关键是利用(1+3+5)2进行解题.

易错点2 没有配凑的观念.

有些问题本身不具备运用柯西不等式的条件,但是我们只要改变一下多项式的形态结构,认清其内在的结构特征,就可以达到利用柯西不等式解题的目的.

例8 已知a、b、c∈R+,且a+b+c=1,则的最大值为________.

解答 将原式进行配凑并结合已知条件a+b+c=1加以计算,即可得到的最大值.

根据柯西不等式,得

当且仅当,即时,的最大值为18.

因此的最大值为

反思 本题给出三个正数满足a+b+c=1,求的最大值.考查了利用柯西不等式求最值的方法.

易错点3 柯西不等式的一般形式不熟练.

柯西不等式中有三个因式,而一般题目中只有一个或两个因式,为了运用柯西不等式,我们需要设法嵌入一个因式(嵌入的因式之和往往是定值),这也是利用柯西不等式的技巧之一.

例9 已知实数a、b、c、d、e满足a+b+c+d+e=8,a2+b2+c2+d2+e2=16,则e的取值范围是______.

解答 由(1+1+1+1)(a2+b2+c2+d2)≥(a+b+c+d)2得到关于e的不等关系,解之即e的取值范围.

由柯西不等式,得(1+1+1+1)(a2+b2+c2+d2)≥(a+b+c+d)2.

即4(16-e2)≥(8-e)2,解得

所以e的取值范围是

反思 此题主要考查不等式的证明问题,其中涉及柯西不等式和基本不等式的应用问题,有一定的技巧性,需要同学们对一般形式的柯西不等式非常熟练.

例10 已知a、b、c为正实数,且a、b、c∈(1,7).

(1)求证

(2)求的最小值.

解答 (1)证明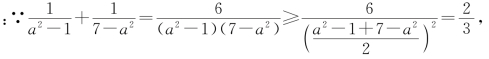

当且仅当a=2时,等号成立.

∴

(2)由柯西不等式,知

当且仅当a=b=c=2时,等号成立.

因此,所求的最小值为1.

反思 本题考查基本不等式的运用,考查柯西不等式,正确运用柯西不等式是关键.

经典训练

1.若直线通过点,则(　).

A.a2+b2≤1　B.a2+b2≥1　C.　D.

2.若m、n、x、y满足m2+n2=a,x2+y2=b,其中a、b为常数,那么mx+ny的最大值为(　).

A.　B.　C.D.

3.若a、b、c、d都为实数,则不等式取等号的条件是(　).

A.ab+dc=0　B.ad+bc=0　C.ab-dc=0　D.ad-bc=0

4.设a、b∈R+,则的最小值为(　).

A.5　B.6　C.8　D.9

5.若a、b是非零实数且则M与N的大小关系为(　).

A.M≥N　B.M>N　C.M≤N　D.M<N

6.函数的最小值为(　).

A.B.10　C.　D.

7.设m、n、x、y>0,且,则u=x+y的最小值为________.

8.函数的最大值为________.

9.设a、b、c、d、m、n都是正实数,,则P与Q的大小关系为_________.

10.若2x+3y=1,则x2+y2的最小值为_________,最小值点为_________.

11.求证:

12.设a+b=1,求证

13.已知p、q∈R+且p3+q3=2,求证:p+q≤2.

14.求函数的最大值.

15.试用柯西不等式求点到直线l:2x+3y-5=0的距离.